| Исходные переменные
| Факторные нагрузки | h2 (общность)
| |
| F1 | F2 | ||
| 1 | 0,97 | 0,20 | 0,99 |
| 2 | 0,86 | 0,20 | 0,78 |
| 3 | -0,18 | 0,76 | 0,62 |
| 4 | 0,09 | 0,74 | 0,56 |
| 5 | 0,26 | 0,69 | 0,55 |
| Собственное значение | 1,79 | 1,70 | 3,5 |
| Доля дисперсии | 0,36 | 0,34 | 0,7 |
Не рассматривая пока шаги, приводящие к этому результату, попытаемся проинтерпретировать полученные данные (интерпретация фактора производится через исходные переменные). В нашем примере по фактору 1 (F 1) максимальные нагрузки имеют переменные 1 и 2. Следовательно, фактор 1 и определяется этими переменными. Поскольку переменная 1 — счет в уме, а переменная 2 — продолжение числового ряда, то фактору 1 может быть присвоено название «арифметические способности», как показателю легкости оперирования числовым материалом. Точно так же фактору 2 можно присвоить название «вербальные способности», как показателю словесного понимания. Нетрудно заметить, что переменные, определяющие фактор, сильнее связаны друг с другом, чем с другими переменными (табл. 1). Так, переменные 1 и 2, определяющие фактор 1, сильнее связаны друг с другом, чем с переменными 3, 4 и 5. Таким образом, за взаимосвязью пяти исходных измерений способностей при помощи факторного анализа обнаруживается действие двух латентных переменных (факторов).
Интерпретация факторов — одна из основных задач факторного анализа. Ее решение заключается в идентификации факторов через исходные переменные. Эта идентификация и осуществляется по результатам обработки, представленным в табл. 40.
Каждый фактор идентифицируется по тем переменным, с которыми он в наибольшей степени связан, то есть по переменным, имеющим по этому фактору наибольшие нагрузки. Идентификация фактора заключается, как правило, в присвоении ему имени, обобщающего по смыслу наименования входящих в него переменных.
Если исследователя интересует только структура измеренных признаков, на этом факторный анализ завершается. Продолжая факторный анализ, исследователь далее может вычислить значения факторов для испытуемых, например, с целью их дифференциации по преобладанию арифметических или вербальных способностей.
Выбирая факторный анализ как средство изучения корреляций, исследователь должен отдавать себе отчет в том, что это один из самых сложных и трудоемких методов. Зачастую нет веских оснований предполагать наличие факторов как скрытых причин изучаемых корреляции, и задача заключается лишь в обнаружении группировок тесно связанных переменных. Тогда целесообразнее вместо факторного анализа использовать кластерный анализ корреляций. Помимо простоты, кластерный анализ обладает еще одним преимуществом: его применение не связано с потерей исходной информации о связях между переменными, что неизбежно при факторном анализе. И уже после выделения групп тесно связанных переменных можно попытаться применить факторный анализ для их объяснения.
Итак, можно сформулировать основные задачи факторного анализа:
1. Исследование структуры взаимосвязей переменных. В этом случае каждая группировка переменных будет определяться фактором, по которому эти переменные имеют максимальные нагрузки.
2. Идентификация факторов как скрытых (латентных) переменных — причин взаимосвязи исходных переменных.
3. Вычисление значений факторов для испытуемых как новых, интегральных переменных. При этом число факторов существенно меньше числа исходных переменных. В этом смысле факторный анализ решает задачу сокращения количества признаков с минимальными потерями исходной информации.
Исходным материалом для факторного анализа является корреляционная матрица. В результате анализа мы получаем таблицу, которая выглядит следующим образом:
Таблица 41
Факторные нагрузки
| Исходные переменные
| Факторные нагрузки | h2 (общность)
| |
| F1 | F2 | ||
| 1 | а11 | а21 | h2 1 |
| 2 | а12 | а22 | h2 2 |
| 3 | а13 | а23 | h2 3 |
| 4 | а14 | а24 | h2 4 |
| 5 | а15 | а25 | h2 5 |
| Собственное значение | … | … | … |
| Доля дисперсии | … | … | … |
Основное содержание табл. 41 — величины а11 ... а25 — факторные нагрузки переменных 1 ... 5 (строки) по факторам 1 и 2 (столбцы). Факторные нагрузки — аналоги коэффициентов корреляции, показывают степень взаимосвязи соответствующих переменных и факторов: чем больше абсолютная величина факторной нагрузки, тем сильнее связь переменной с фактором, тем больше данная переменная обусловлена действием соответствующего фактора.
Фактор – это искусственный статистический показатель, который получается в результате преобразований корреляционной матрицы.
Процедура извлечения факторов называется факторизацией.
Факторные нагрузки (факторные веса) – коэффициенты корреляции каждого фактора с каждой переменной.
Каждый фактор идентифицируется по тем признакам, с которыми он в наибольшей степени связан (наибольшие нагрузки). Идентификация фактора заключается, как правило, в присвоении ему имени обобщающего по смыслу наименования входящих в него переменных.
Общность переменной – это сумма квадратов факторных нагрузок. Она показывает часть дисперсии признака, которая является общей для двух (в данном случае) переменных.
Переменные с большей общностью имеют значительно большую долю дисперсии с одним или несколькими факторами.
Низкая общность означает, что ни один из факторов не имеет совпадающей доли дисперсии с данной переменной. Низкая общность может свидетельствовать о том, например, что переменная измеряет нечто качественно отличающееся от других признаков, включённых в анализ.
Собственные значения фактора – это значимость каждого из факторов.
В нижней строчке приводится доля дисперсии фактора – часть дисперсии в выборке, которая объясняется данным фактором.
Факторный анализ бывает двух видов:
Эксплораторный-разведочный.
Используется для анализа результатов исследования для того, чтобы сформулировать рабочие гипотезы о причинах обнаруженных связей. Выполняется на ориентировочной стадии работы.
Конфирматорный.
Применяется на более поздних стадиях исследования для проверки гипотез. Когда в рамках какой-либо теории или модели сформулированы чёткие гипотезы, факторы между переменными и факторами достаточно определены, и исследователь может их прямо указать. В этом случае факторный анализ является средством проверки соответствия сформулированной гипотезы полученным эмпирическим данным.
Факторный анализ может выполняться различными методами (о различии методов см. учебник Наследова).
Анализ главных компонент. При использовании этого метода общность каждой переменной получается автоматически, путем суммирования квадратов ее нагрузок по всем главным компонентам. Вопрос о приближении восстановленных коэффициентов корреляции к исходным корреляциям не решается. В результате факторная структура искажается в сторону преувеличения абсолютных величин факторных нагрузок.
Факторный анализ образов — это метод главных компонент, применяемый к так называемой редуцированной корреляционной матрице, у которой вместо единиц на главной диагонали располагаются оценки общностей. Общность каждой переменной оценивается предварительно, как квадрат коэффициента множественной корреляции (КМК) этой переменной со всеми остальными. Такая оценка, с точки зрения теоретиков факторного анализа, приводит к более точным результатам, чем в анализе главных компонент. Но значения общностей недооцениваются, что также приводит к искажениям факторной структуры, хотя и меньшим, чем в предыдущем случае.
Метод главных осей позволяет получить более точное решение. На первом шаге общности вычисляются по методу главных компонент. На каждом последующем шаге собственные значения и факторные нагрузки вычисляются исходя из предыдущих значений общностей. Окончательное решение получается при выполнении заданного числа итераций или достижении минимальных различий между общностями на данном и предыдущем шагах.
Метод не взвешенных наименьших квадратов — минимизирует квадраты остатков (разностей) исходной и воспроизведенной корреляционных матриц (вне главной диагонали). Процесс повторяется многократно до тех пор, пока не достигается минимально возможная разница между исходными и вычисленными корреляциями при заданном числе факторов. Метод, по определению, дает минимальные ошибки факторной структуры при фиксированном числе факторов. Реализация метода в компьютерных программах позволяет проверить расхождения между исходными и вычисленными корреляциями. Наличие многочисленных расхождений может служить дополнительным аргументом в пользу увеличения числа факторов.
Обобщенный метод наименьших квадратов — отличается от предыдущего тем, что для каждой переменной вводятся специальные весовые коэффициенты. Чем больше общность переменной, тем в большей степени она влияет на факторную структуру (имеет больший вес). Это соответствует основному принципу статистического оценивания, по которому менее точные наблюдения учитываются в меньшей степени. В этом — основное преимущество этого метода перед остальными.
Метод максимального правдоподобия также направлен на уменьшение разности исходных и вычисленных корреляций между признаками. Дополнительно этот метод позволяет получить важный показатель полноты факторизации — статистическую оценку «качества подгонки». Однако следует помнить, что этот критерий, как и остальные формальные критерии, является дополнительным. Окончательное же решение о числе факторов принимается после содержательной интерпретации факторной структуры.
Вряд ли возможно дать общие рекомендации о преимуществе или недостатке того или иного метода. Можно лишь отметить, что анализ главных компонент дает наиболее грубое решение, а метод максимального правдоподобия позволяет статистически оценить минимально возможное число факторов для данного набора переменных. По-видимому, в каждом конкретном случае стоит сравнивать результаты применения разных методов и выбирать тот, который позволяет получить наиболее простую и доступную интерпретации факторную структуру.
Основные этапы факторного анализа:
Выбор исходных данных.
А) Факторный анализ применяется для признаков, измеренных по интервальной или пропорциональной шкалам.
Б) Все признаки должны иметь нормальное распределение.
В) Между признаками недопустимы функциональные зависимости.
Г) Нежелательны корреляции, близкие к единице («1»).
Д) В исходной матрице должно быть хотя бы несколько корреляций, по абсолютной величине выше, чем 0,3.
Е) Нельзя включать признаки, измеренные по шкале наименований.
Ж) Включение в анализ порядковых данных (ординальные шкалы) нежелательно, но допустимо; однако исследователь должен отдавать себе отчёт в том, что характер искажений нам неизвестен. В общем случае желательно перейти к единой шкале для всех.
З) Выборка должны быть достаточно большой. Некоторые авторы рекомендуют не менее 100 человек. Число признаков должно быть в 3 или 4 раза меньше, чем количество испытуемых.
Предварительное решение проблемы числа факторов.
А) Указать приблизительное число факторов и получить график собственных значений факторов.
|
|
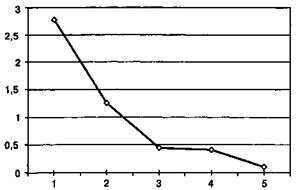
Рис. 21. График собственных значений факторов
На графике находится точка перегиба ломаной линии; этой точке соответствует k факторов; возможное число факторов будет равно: k ±1.
Данный способ называется метод отсеивания Кеттела.
Б) Критерий величины собственного значения фактора.
Выбирается число факторов, для которых собственные значения больше 1. На этом этапе рекомендуется использовать метод факторного анализа – анализ главных компонент, и проверить несколько гипотез о числе факторов. Начинать следует с максимально возможного числа факторов; с учётом обоих критериев уменьшить их число.
Окончательное решение о числе факторов принимается только после интерпретации факторов.
Дата: 2019-11-01, просмотров: 508.