Назначение критерия
Критерий предназначен для сопоставления двух распределений:
а) эмпирического с теоретическим, например, равномерным или нормальным;
б) одного эмпирического распределения с другими эмпирическим распределением.
Критерий позволяет найти точку, в которой сумма накопленных расхождений между двумя распределениями является наибольшей, и оценить достоверность этого расхождения.
Если различия между двумя распределениями существенны, то в какой-то момент разность накопленных частот достигнет критического значения, и мы сможем признать различия статистически достоверными. В формулу критерия включается эта разность. Чем больше эмпирическое значение, тем более существенны различия.
Ограничения критерия:
1. Критерий требует, чтобы выборка была достаточно большой. При сопоставлении двух эмпирических распределений необходимо, что бы N1,2 ≥50. Сопоставление эмпирического распределения с теоретическим иногда допускается при N1,2 ≥5.
2. Разряды должны быть упорядочены по нарастанию или убыванию какого-либо признака. Они обязательно должны отражать какое-то однонаправленное его изменение.
3. Критерий применяется для сравнения признаков, измеренных по шкалам порядка, интервальной или пропорциональной. Мы не можем накапливать частоты по разрядам, которые отличаются лишь качественно и не представляют собой шкалы порядка. Во всех тех случаях, когда разряды представляют собой не упорядоченные по возрастанию или убыванию какого-либо признака категории, нам следует применять метод хи-квадрат.
Алгоритм расчета критерия
Расчет критерия при сопоставлении двух эмпирических распределений[11]
1. Расчеты целесообразно провести, пользуясь следующей таблицей.
Таблица 34
| № п/п | xi | f1i | f2i | p1i | p2i | P1i | P2i | |di| |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| ….. | ||||||||
| N |
Занести в таблицу значения признака (наименования разрядов для сгруппированного распределения) — второй столбец, соответствующие им эмпирические частоты, полученные в распределении 1 (третий столбец) и в распределении 2 (четвертый столбец).
2. Подсчитать эмпирические частости (относительные частоты) по каждому разряду для распределения 1 по формуле:
 ,
,
где f1i - эмпирическая частота для данного значения (интервала);
N1 - количество наблюдений в выборке.
Занести эмпирические частости распределения 1 в пятый столбец.
3. Подсчитать эмпирические частости по каждому разряду для распределения 2 по формуле:
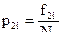 ,
,
где f2i - эмпирическая частота для данного значения (интервала);
N2 - количество наблюдений в выборке.
Занести эмпирические частости распределения 2 в шестой столбец таблицы.
4. Подсчитать накопленные эмпирические частости для распределения 1 по формуле:

где Рi-1 – относительная частота, накопленная для предыдущего значения (интервала);
i - порядковый номер значения (интервала);
рi – абсолютная частота данного значения (интервала).
Полученные результаты записать в седьмой столбец.
5. Подсчитать накопленные эмпирические частости для распределения 2 по той же формуле и записать результат в восьмой столбец.
6. Подсчитать разности между накопленными частостями по каждому разряду di= Р1i – Р2i. Записать в девятый столбец абсолютные величины разностей (без их знака). Обозначить их как |di|.
7. Определить по седьмому столбцу наибольшую абсолютную величину разности |dmax|.
8. Подсчитать значение критерия по формуле:
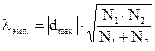 ,
,
где |dmax|- наибольшая абсолютная величина разности накопленных частот;
N1- количество наблюдений в первой выборке;
N2 – количество наблюдений во второй выборке.
5. Правило вывода:
Критические значения критерия Колмогорова-Смирнова постоянны:
λкрит.= 1,36 для уровня значимости р=0,95
λкрит.= 1,63 для уровня значимости р=0,99
Если λэмп. ≥ λкрит., то различия между распределениями статистически достоверны.
Если λэмп. < λкрит., то различия между распределениями статистически не достоверны.
Контрольные вопросы:
- Какие задачи решает критерий хи-квадрат Пирсона?
- Можно ли использовать критерий хи-квадрат Пирсона для сравнения распределений признаков, измеренных по номинативной шкале?
- Каково правило принятия решения в критерии хи-квадрат Пирсона?
- Какие задачи решает критерий Колмогорова-Смирнова?
- Какова область применения данного критерия?
- Можно ли использовать критерий Колмогорова-Смирнова для сравнения распределений признаков, измеренных по шкале наименований?
- Как найти теоретические частоты при сравнении эмпирического распределения и равномерного распределения?
- Как найти теоретические частоты при сравнении эмпирического распределения и нормального распределения?
- Каково правило принятия решения в критерии Колмогорова-Смирнова?
МАТЕРИАЛЫ ДЛЯ ИЗУЧЕНИЯ ТЕМЫ:
а) основная литература:
1. Ермолаев О. Ю. Математическая статистика для психологов. — М., 2008. — Стр. 159-164.
2. Кутейников А.Н. Математические методы в психологии. – СПб, 2008. — Стр. 85-103.
3. Сидоренко Е. В. Методы математической обработки в психологии. — СПб.,2004. — Стр. 110-156.
б) дополнительная литература:
Суходольский Г. В. Основы математической статистики для психологов. — СПб., 1998. — 294-305.
Дата: 2019-11-01, просмотров: 383.