Понятие многофункциональных статистических критериев. Критерий φ* — угловое преобразование Фишера: назначение критерия, его описание, область применения, алгоритм применения. Критерий Макнамары: назначение критерия, его описание, область применения, алгоритм расчета. Биномиальный критерий m: назначение критерия, его описание, область применения, алгоритм применения. Многофункциональные критерии как эффективные заменители традиционных критериев. Алгоритм выбора многофункциональных критериев.
Методические рекомендации к изучению темы
При изучении данной темы необходимо учесть то, что оба критерия непараметрические, они оперируют частотами абсолютными или процентными. Обратите особое внимание на правила принятия решения для рассмотренных критериев: эти правила могут быть противоположны. Внимательно изучите ограничения в применении критериев.
После изучения материала лекции ответьте на контрольные вопросы, ответы занесите в конспект. При самостоятельном изучении биномиального критерия материал в конспекте должен быть изложен в следующей последовательности: назначение критерия, ограничения в его использовании, алгоритм расчета критерия с указанием правила принятия решения.
Материалы лекции.
Многофункциональные статистические критерии — это критерии, которые могут использоваться по отношению к самым разнообразным данным, выборкам и задачам. Это означает, что данные могут быть представлены в любой шкале, начиная от шкалы наименований. Выборки могут быть как зависимыми, так и независимыми. Эти критерии позволяют решать задачи сравнения уровней выраженности признака, оценки сдвигов значений и сравнения распределений.
Многофункциональные критерии построены на сопоставлении долей, выраженных в долях единицы или в процентах. Суть критериев состоит в определении того, какая доля наблюдений (реакций, выборов, испытуемых) в данной выборке характеризуется интересующим исследователя эффектом и какая доля этим эффектом не характеризуется.
Критерий φ *применяется в тех случаях, когда обследованы две выборки испытуемых, биномиальный критерий m — в тех случаях, когда обследована лишь одна выборка испытуемых.
Критерий φ* — «Угловое преобразование» Фишера
Назначение критерия
Критерий Фишера предназначен для сопоставления двух выборок по частоте встречаемости интересующего исследователя эффекта.
Критерий оценивает достоверность различий между процентными долями двух выборок, в которых зарегистрирован интересующий нас эффект.
Суть углового преобразования Фишера состоит в переводе процентных долей в величины центрального угла, который измеряется в радианах. Большей процентной доле будет соответствовать больший угол φ, а меньшей доле – меньший угол, но соотношения здесь не линейные: 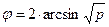 , где р — процентная доля, выраженная в долях единицы (см. рис. 20).
, где р — процентная доля, выраженная в долях единицы (см. рис. 20).
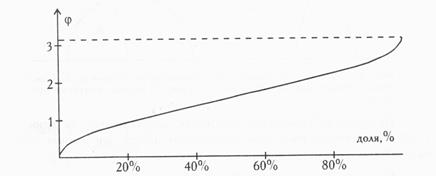
Рис. 20. График зависимости угла φ от процентной доли
При увеличении расхождения между углами φ1 и φ2 и увеличения численности выборок значение критерия возрастает. Чем больше величина φ*, тем более вероятно, что различия достоверны.
Ограничения критерия φ*
1. Ни одна из сопоставляемых долей не должна быть равной нулю. Формально нет препятствий для применения метода φ* в случаях, когда доля наблюдений в одной из выборок равна 0. Однако в этих случаях результат может оказаться неоправданно завышенным.
2. Верхний предел в критерии φ* отсутствует — выборки могут быть сколь угодно большими.
Нижний предел — 2 наблюдения в одной из выборок. Однако должны соблюдаться следующие соотношения в численности двух выборок:
а) если в одной выборке всего 2 наблюдения, то во второй должно быть не менее 30:
N1=2 ® N2≥30
б) если в одной из выборок всего 3 наблюдения, то во второй должно быть не менее 7:
N1=3 ® N2≥7
в) если в одной из выборок всего 4 наблюдения, то во второй должно быть не менее 5:
N1=4 ® N2≥5
г) при N1, N2≥5 возможны любые сопоставления.
В принципе возможно и сопоставление выборок, не отвечающих этому условию, например, с соотношением N1=2 и N2=15, но в этих случаях не удастся выявить достоверных различий.
Других ограничений у критерия φ* нет.
Алгоритм расчета критерия φ*
1. Определить те значения признака, которые будут критерием для разделения испытуемых на тех, у кого «есть эффект» и тех, у кого «нет эффекта». Если признак измерен количественно, использовать критерий λ для поиска оптимальной точки разделения.
2. Начертить четырехклеточную таблицу (таблица 35) из двух столбцов и двух строк. Первый столбец - «есть эффект»; второй столбец - «нет эффекта»; первая строка сверху – 1 группа (выборка); вторая строка – 2 группа (выборка).
Таблица 35
| Выборка | «Есть эффект» | «Нет эффекта» | Σ |
| 1 выборка | |||
| 2 выборка | |||
| Σ |
3. Подсчитать количество испытуемых в первой группе, у которых «есть эффект», и занести это число в левую верхнюю ячейку таблицы.
4. Подсчитать количество испытуемых в первой выборке, у которых «нет эффекта», и занести это число в правую верхнюю ячейку таблицы. Подсчитать сумму по двум верхним ячейкам. Она должна совпадать с количеством испытуемых в первой группе.
5. Подсчитать количество испытуемых во второй группе, у которых «есть эффект», и занести это число в левую нижнюю ячейку таблицы.
6. Подсчитать количество испытуемых во второй выборке, у которых «нет эффекта», и занести это число в правую нижнюю ячейку таблицы. Подсчитать сумму по двум нижним ячейкам. Она должна совпадать с количеством испытуемых во второй группе (выборке).
7. Определить процентные доли испытуемых, у которых «есть эффект», путем отнесения их количества к общему количеству испытуемых в данной группе (выборке). Записать полученные процентные доли соответственно в левой верхней и левой нижней ячейках таблицы в скобках, чтобы не перепутать их с абсолютными значениями.
8. Проверить, не равняется ли одна из сопоставляемых процентных долей нулю. Если это так, попробовать изменить это, сдвинув точку разделения групп в ту или иную сторону. Если это невозможно или нежелательно, от казаться от критерия φ* и использовать критерий c2.
9. Определить по специальной таблице (приложение 9) величины углов для каждой из сопоставляемых процентных долей φ1 и φ2.
10. Подсчитать эмпирическое значение φ* по формуле:
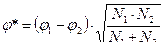
где φ* — расчетное значение критерия;
φ1— угол, соответствующий большей процентной доле;
φ2— угол, соответствующий меньшей процентной доле;
N1— количество наблюдений в выборке 1;
N2— количество наблюдений в выборке 2.
11. Правило принятия решения:
Сопоставить полученное значение φ* с критическими значениями:
φ*=1,64 на уровне значимости р=0,95 и φ*=2,31 на уровне значимости р=0,99.
Если φ*расч> φ*табл, то различия между сравниваемыми процентными долями статистически значимы.
Если φ*расч≤ φ*табл, то различия между сравниваемыми процентными долями статистически незначимы.
Критерий Макнамары
Назначение критерия
Критерий Макнамары очень прост, однако его использование имеет некоторые особенности и требует определенных навыков в статистических расчетах и работе с таблицами критических величин. Этот критерий относится также к числу непараметрических критериев и предназначен для работы с данными, полученными в самой простой из номинальных в дихотомической шкале. Критерий позволяет оценить различия между значениями признака, полученные в двух замерах на одной и той же выборке испытуемых.
Дата: 2019-11-01, просмотров: 600.