Параметрический критерий t Стьюдента для сравнения результатов количественного измерения: алгоритм применения для зависимых выборок.
Непараметрические критерии. Критерий знаков: назначение критерия его описание, область применения, алгоритм применения. Критерий Вилкоксона: для сравнения результатов количественного измерения. Критерий Фридмана: для сравнения результатов количественного измерения. Критерий тенденций Пейджа: для сравнения результатов количественного измерения.
Методические рекомендации к изучению темы
При изучении данной темы необходимо учесть то, что рассматриваются две группы критериев: оценка выраженности признака и оценка сдвига значений признака. Обратите особое внимание на правила принятия решения для рассмотренных критериев: эти правила могут быть противоположны. Внимательно изучите ограничения в применении критериев.
При изучении данной темы необходимо обратить внимание на то, что критерий Стьюдента применяется для сравнения любых двух параметров распределений, однако в лекциях приведены формулы лишь для сравнения среднего арифметического значения и стандартного отклонения. Внимательно изучите ограничения в применении критерии Стьюдента. Обратите внимание, что одно из ограничений касается нормальности распределения признака в выборках.
При самостоятельном изучении критерия Фридмана и критерия тенденций Пейджа материал в конспекте должен быть изложен в следующей последовательности: назначение критерия, ограничения в его использовании, алгоритм расчета критерия с указанием правила принятия решения.
После изучения материала лекции ответьте на контрольные вопросы и выполните самостоятельные задания, ответы занесите в конспект.
Материалы лекции.
Нередко, сравнивая «на глазок» результаты «до» и «после» какого либо воздействия (например, тренинга), психолог видит тенденции повторного измерения — большинство показателей может увеличиваться или, напротив, уменьшаться. Наиболее простым путем оценки различий, казалось бы, является подсчет процентов в изменениях в ту или другую сторону «до» и «после» и сравнение полученных процентов между собой. На основе этого сравнения можно было бы придти к заключению, что если наблюдаются различия в процентах, то имеет место различие и в сравниваемых психологических характеристиках «до» и «после». Подобный подход категорически неприемлем, поскольку для процентов нельзя определить уровень достоверности в их различиях. Делать какие либо выводы из экспериментального материала возможно только на основе статистических процедур, специально сконструированных так, что на их основе можно определить уровень достоверности различий. Проценты, взятые сами по себе, не дают возможности делать статистически достоверные выводы. Поэтому, для того чтобы доказать эффективность какого-либо воздействия, необходимо выявить статистически значимую тенденцию в смещении (сдвиге) показателей.
При работе с этой группой критериев необходимо ввести понятие сдвига значений.
Сдвигом значений называется разность между показателями во втором и первом замерах (или «после – до»). Сдвиг называется типичным в какую-то сторону, если данный знак разности встречается в выборке чаще; нетипичным — если данный знак разности встречается реже. Сдвиги, при которых разность значений равна 0, называются нулевыми.
Параметрический критерий Стьюдента для сравнения зависимых выборок
Назначение критерия
Критерий Стьюдента применяется:
А) для сравнения любых двух параметров распределений или проверки гипотез о случайности различий между параметрами (Н0);
Б) для интервального оценивания (является ли параметр, полученный на выборочной совокупности, параметром генеральной совокупности);
В) для оценки статистической значимости мер связи (коэффициентов корреляции).
Ограничения в использовании критерия:
1. Критерий Стьюдента применяется для сравнения параметров признаков, измеренным по интервальной или пропорциональной шкалам.
2. Распределение признака должно быть нормальным.
3. Ограничений по объему выборки нет
Алгоритм расчета критерия Стьюдента для зависимых выборок:
1) Для удобства расчетов целесообразно составить таблицу следующего вида:
Таблица 31
| № | X1i | X2i | di | di- 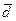
| (di- 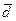 )2 )2
|
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | |||||
| 2 | |||||
| ….. | |||||
| N | |||||
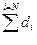
| 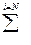 (di- (di- 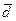 )2 )2
|
В этой таблице:
столбик 1 — номера испытуемых по порядку в списке;
столбик 2 — X1i — значения признака в данной выборке в ситуации 1;
столбик 3 — X2i — значения признака в данной выборке в ситуации 2.
2) Для каждой пары измерений в двух ситуациях находим их разницу (сдвиг значений) — столбик 4:
di = X2i – X1i
3) Для выборки значений di определяем параметры: средний арифметический сдвиг и стандартное отклонение сдвига.
Для среднего арифметического необходимо найти сумму всех сдвигов (по столбику 4) и подставить в формулу:
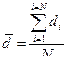
Для вычисления стандартного отклонения необходимо:
а) найти разность каждого значения сдвига и среднего арифметического сдвига — столбик 5;
б) возвести каждую разность в квадрат — столбик 6;
в) найти сумму квадратов разностей (по столбику 6) и подставить найденную сумму в формулу:
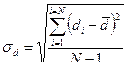
4) Вычисляем расчетное значение критерия Стьюдента по формуле:
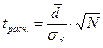
5) Находим число степеней свободы:
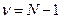
Правило принятия решения:
Расчетное значение критерия Фишера необходимо сравнить с критическим (табличным) значением (см. таблицу критических значений критерия Фишера), которое находится в зависимости от двух значений — числа степеней свободы для каждой выборки. Число степеней свободы находится по следующим формулам:
ν1 = N1 – 1 и ν2 = N2 – 1
Если Fрасч. > Fкритич., то различия между дисперсиями статистически значимы. Если Fрасч. ≤ Fкритич., то дисперсии статистически не различаются.
Дата: 2019-11-01, просмотров: 348.