Решатель optim
Решатель optimпредназначен для решения задачи нелинейной оптимизации f( X ), где X является вектором, а f( X ) функцией, возвращающей скаляр. Функция optim использует Квази-Ньютоновские методы, основанные на различных алгоритмах, в том числе на BFGS -алгоритме, который представляет собой алгоритм высокой точности для локальной оптимизации. Пространство допустимых решений этой функции может быть и ограниченное – задача нелинейной оптимизации с ограничениями (или условная оптимизация):
min f(X), приb inf <= X<= b sup,
где binf – нижняя граница, а bsup – верхняя граница X.
Для вычисления значений целевой функции и её производных функция optimиспользует вспомогательную функцию costf. Имя этой функции входит в состав аргументов в качестве указателя на функцию. Заметим, что функция costf является внешней, и может быть написана на языках Scilab, C++ или Fortran.
В случае если costf является sce-функцией, то обращение к ней может иметь следующий формат:
[f,g,ind]=costf(X,ind),
где X – вектор значений текущей точки, ind – параметр, предназначенный для связи функции costfс функцией optim(если значение ind равно 2 , 3 или 4 то функция с ostfобеспечивает поиск минимума, если ind =1, то в функция optimне выполняется), f – вещественное значение целевой функции в точке X, а g – вектор, содержащий значения частных производных целевой функции (или, в случае одномерной оптимизации, значение производной), вычисляемых с использованием функции numdervative(f, X ).
Выходное значение параметра indпоказывает причину завершения работы функции costf, причем, если ind <0, то это значит, что f не может являться оценкой X , а ind =0 означает прерывание процесса оптимизации.
Функция optimможет быть вызвана одним из следующих форматов:
fopt= optim (costf,X0)
fopt= optim (costf,<contr>,X0,algo,df0,mem,work,<stop>,iprint=iflag)
[fopt,xopt]= optim (…)
[fopt,xopt,gopt]= optim (…)
[fopt, xopt, gopt, work] = optim (…)
[fopt, xopt, gopt, work, iters] = optim (…)
[fopt, xopt, gopt, work, iters, evals]= optim (…)
[fopt, xopt, gopt, work, iters, evals, err]= optim (…)
fopt,xopt,gopt,work,iters,evals,err,ti,td= optim (…,params="si","sd")
Набор обязательных входных параметров:
сostf – функция, вычисляющая целевую функцию и частные производные (или производную в случае одномерной
оптимизации);
X 0 – вещественный вектор, состоящий из начальных значенийX.
Необязательные входные параметры:
<сontr>– последовательность (список) параметров, содержащий границы X: "b", binf и bsup, где binf и bsup – вещественные вектора с таким же размером, что и X 0;
аlgo – строка, указывающая используемые доступные алгоритмы (по умолчанию – "qn"):
"qn" – Квази-Ньютоновский BFGS;
"gc" – ограниченная память BFGS;
"nd" – не используются производные и не учитываются
ограничения по X.
df0 – вещественный скаляр, представляющий значение f на первой
итерации (по умолчанию df0=1).
m em – целое число переменных, используемых для матрицы Гессе (по
умолчанию mem=10);
<stop>– последовательность (список) параметров, управляющий
cходимостью алгоритма:
" ar ", nap
" ar ", nap , iter
"ar", nap, iter, epsg
"ar", nap, iter, epsg, epsf
"ar", nap,iter, epsg, epsf, epsx
где: nap – максимальное количество допустимых
вызовов costf (по умолчанию nap=100);
iter – максимальное количество итераций (по умолчанию
iter=100);
e psg – порог градиентной нормы (по умолчанию epsg=%eps);
e psf – порог контроля снижения f (по умолчанию epsf=0);
e psx – порог контроля изменения X (по умолчанию epsx=0),
"iprint=iflag" – именованный аргумент, используемый для установки режима трассировки выходных данных (по умолчанию iprint=0, режим, при котором печатаются сообщения), причем, если iprint больше или равно 1, выводится больше информации, в зависимости от выбранного алгоритма:
Если iflag<0, то целевая функция вычисляется в каждой из m итераций, с ind=1.
Выходные параметры:
f opt – значение целевой функции в точке x opt;
x opt – вектор аргументов, обеспечивших оптимальное значение
функции;
gopt – градиент целевой функции (или производной в случае одномерной оптимизации) в точке x opt;
work – рабочий массив перезапуска для Квази-Ньютоновских методов.
i ters – скаляр, число итераций, которое отображается при iprint=2.
e vals – скаляр, число вычислений функции cost, которое отображается
при iprint=2.
e rr – скаляр, индикатор завершения, может иметь следующие
значения:
· err=1 – норма вычисленного градиента ниже допустимого;
· err=2 – на последней итерации f уменьшается;
· err=3 – оптимизация останавливается из-за слишком малых
изменений для X;
· err=4 – остановка: максимальное количество обращений к f;
· err=5 – остановка: максимальное количество итераций;
· err=6 – остановка: слишком маленькие изменения в
направлении градиента;
· err=7 – остановка: во время расчета направления спуска;
· err=8 – остановка: во время расчета оценки матрицы Гессе;
· err=9 – окончание оптимизации, успешное завершение;
· err=10 – успешное окончание оптимизации (линейный поиск
не выполняется).
Каждый алгоритм, реализованный в optim, имеет свои собственные критерии завершения, которые могут использовать параметры, полученные от пользователя, такие как: nap , iter , epsg , epsf и epsx.
Рассмотрим пример использования решателя optim для случая решения задачи оптимизации одномерной функции f ( x )= x 4 +3 x 3 -13 x 2 -6 x +26, имеющей на отрезке [-4;-2] единственный минимум (исследование которой приведено выше на рис. 2.7.1-2 и 2.7.1-3), выбрав в качестве начальной точки х0=-3
(рис. 2.7.3-1). В нашем случае используется достаточно простой формат функции optim – передается имя вспомогательной функции (costf ) и начальное значение аргумента (х0), а в качестве выходных параметров выступают координаты точки минимума функции f(х).

|
 -->// Нахождение координат точки минимума с использованием решателя optim
-->
-->exec('РИС2731.sce');
-->x0 = -3;
--> // Вычисление координат точки минимума
--> [fmin, xmin] = optim(costf, x0); // Обращение к функции optim
--> disp([fmin, xmin])
-95.089413 -3.8407084
-->// Нахождение координат точки минимума с использованием решателя optim
-->
-->exec('РИС2731.sce');
-->x0 = -3;
--> // Вычисление координат точки минимума
--> [fmin, xmin] = optim(costf, x0); // Обращение к функции optim
--> disp([fmin, xmin])
-95.089413 -3.8407084
|
Рис. 2.7.3-1. Нахождение координат точки минимума функции f ( x )с использованием решателя optim
В примере, приведенном на рис. 2.7.3-1 для вычисления производной используется функция numderivative, что позволяет устранить проблему получения аналитических выражений производных в случае сложного выражения целевой функции. Однако использовать эту функцию совсем необязательно. Так, например, на рис. 2.7.3-2 приведен сценарий, в котором для вычисления значений производной используется аналитическое выражение.

|
Рис. 2.7.3-2. Вычисление производной с использованием
ее математического выражения
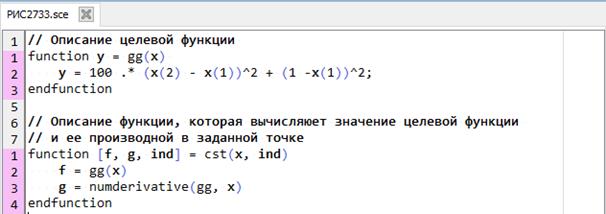
В следующем примере (рис.2.7.3-3) определим координаты точки минимума и значение многомерной функции Розенброка:
f ( x 1 , x 2 )=100(x2-x12)2+(1-x1)2,
с использованием того же упрощенного формата функции optim. Ранее (рис.2.7.1-4) в качестве начального приближения уже был выбран вектор начальных значений [0,0].
|
 --> // Нахождение минимума многомерной функции f(x1,x2)
-->
-->exec('РИС2733.sce', 0);
-->x0 = [0; 0]; // Начальныезначения
--> [f, xopt] = optim(cst, x0); // Обращение к функции optim
disp(f, [xopt']);
1. 1.
.083D-30
--> // Нахождение минимума многомерной функции f(x1,x2)
-->
-->exec('РИС2733.sce', 0);
-->x0 = [0; 0]; // Начальныезначения
--> [f, xopt] = optim(cst, x0); // Обращение к функции optim
disp(f, [xopt']);
1. 1.
.083D-30
|
Рис. 2.7.3-3. Использование функции optim для нахождения координат точки минимума многомерной функции f(x1,x2)
Отметим, что в описанных выше примерах были использованы самые простые форматы функции optim. Однако в процессе вычислений часто представляет интерес: сколько итераций потребовалось для нахождения минимума той или иной функции, причину прекращения итерационного процесса и многие другие моменты, которые могут быть выявлены при использовании других, описанных выше, форматов этой функции.
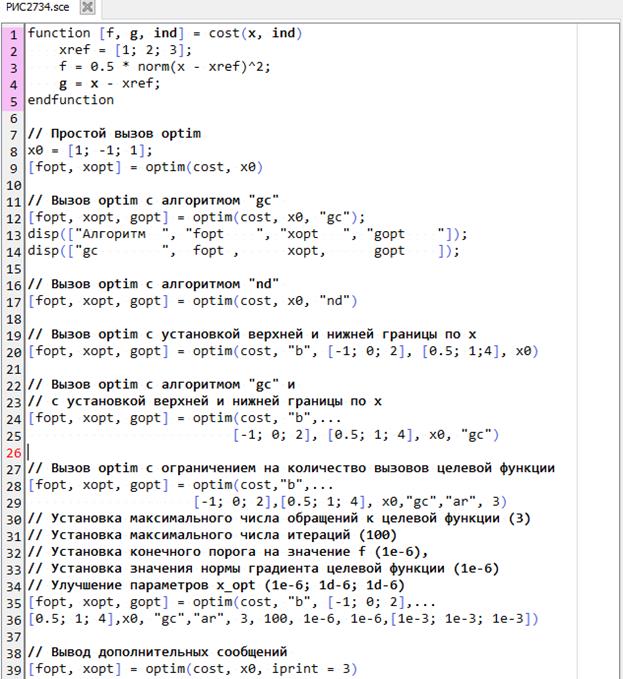
Именно поэтому пользователю, решающему серьезные задачи оптимизации крайне важно рассмотреть и проанализировать результаты выполнения следующего примера (рис. 2.7.3.4), показывающего возможности использования различных (необязательных) параметров функции optim.
| |
|
--> // Загрузка сценария РИС2734 --> // --> // exec('РИС2734.sce', 0) Xopt = 1.2.3.; fopt=0.; gopt= 0.0.0. Xopt = 1. 2. 3.; fopt=0.;gopt= 0.-1.776D-14-1.199D-14 xopt=1. 2. 3.; fopt=2.297D-28; gopt=-0.5-1.0. xopt=0.5 1.3.;fopt=0.625; gopt=-0.5 -1. 0. xopt=0.5 1. 3.;fopt=0.625; gopt=-0.5 -1.5559108 -0.7779554 xopt=0.5 1. 2.2220446 fopt=1.6380365 gopt=-0.5 -1.8308232 -0.9154116 xopt=0.5 1. 2.0845884 fopt=2.2199459 ***** enters -qn code- (without bound cstr) dimension=3, epsq=0.2220446049250313E-15, verbosity level: iprint=3 max number of iterations allowed: iter=100 max number of calls to costf allowed: nap=100 ------------------------------------------------ iter num 1, nb calls=1, f=6.500 linear search: initial derivative=-3.606 step length=0.1000E-01, df=-0.4261, derivative=-3.485 step length=0.1000, df=-3.611, derivative=-2.404
iter num 2, nb calls=3, f=2.889 linear search: initial derivative=-2.404 step length=1.000,df=-2.889,derivative=0.3695E-15
iter num 3, nb calls=4, f=0.9861E-30 linear search: initial derivative=-0.1380E-14 step length=1.000,df=0.4142E-29, derivative=0.3192E-14 step length=0.2996,df=-0.9861E-30,derivative=0.0000E+00
iter num 4, nb calls=6, f=0.0000E+00 ***** leaves -qn code-, gradient norm=0.0000000000000000E+00 optim: Норма проектируемого градиента ниже, чем 0. xopt=1.2.3.fopt=0. | |
x0 = 1. -1. 1.
xopt = 1. 2. 3.
fopt = 0.
gopt = 0. 0. 0.
xopt = 1. 2. 3.
fopt = 0.
gopt = 0. -1.776D-14 -1.199D-14
xopt = 1. 2. 3.
fopt = 2.297D-28
gopt = -0.5 -1. 0.
xopt = 0.5 1. 3.
fopt = 0.625
gopt = -0.5 -1. 0.
xopt = 0.5 1. 3.
fopt = 0.625
gopt = -0.5 -1.5559108 -0.7779554
xopt = 0.5 1. 2.2220446
fopt = 1.6380365
gopt = -0.5 -1.8308232 -0.9154116
xopt = 0.5 1. 2.0845884
fopt = 2.2199459
***** enters -qn code- (without bound cstr)
dimension= 3, epsq= 0.2220446049250313E-15, verbosity level: iprint= 3
max number of iterations allowed: iter= 100
max number of calls to costf allowed: nap= 100
------------------------------------------------
iter num 1, nb calls= 1, f= 6.500
linear search: initial derivative= -3.606
step length= 0.1000E-01, df=-0.4261 , derivative= -3.485
step length= 0.1000 , df= -3.611 , derivative= -2.404
iter num 2, nb calls= 3, f= 2.889
linear search: initial derivative= -2.404
step length= 1.000, df= -2.889, derivative= 0.3695E-15
iter num 3, nb calls= 4, f= 0.9861E-30
linear search: initial derivative=-0.1380E-14
step length= 1.000, df= 0.4142E-29, derivative= 0.3192E-14
step length= 0.2996, df=-0.9861E-30, derivative= 0.0000E+00
iter num 4, nb calls= 6, f= 0.0000E+00
***** leaves -qn code-, gradient norm= 0.0000000000000000E+00
optim: Норма проектируемого градиента ниже, чем 0.
xopt = 1. 2. 3.
fopt = 0.
Рис. 2.7.3-4. Применение дополнительных параметров при использовании функции optim
Решатель fminsearch
Решатель f minsearch – вычисляет безусловный минимум функции по алгоритму Нелдера-Мида и имеет следующие форматы [13]:
X=fminsearch(costf, х 0)
X=fminsearch(costf, х 0,options)
[X,fval]=fminsearch(costf, х 0,options)
[X,fval,exitflag]=fminsearch(costf, х 0,options)
[X,fval,exitflag,output]=fminsearch(costf, х 0,options)
Этот решатель является алгоритмом прямого поиска, не использующим производную целевой функции, а основан на обновлении симплекса, который является набором k>=n+1 вершин, где каждая вершина связана с одной точкой и одним значением функции. Алгоритм создан на базе neldermead компонент [13].
Рассмотрим подробнее назначение параметров:
Входные параметры:
сostf – внешняя функция, которая возвращает значение целевой
функции и имеет следующий заголовок f=costf( X ),
где X– текущая точка;
f – значение целевой функции;
X 0 – матрица начальных значений;
options – структура данных, содержащая настраиваемые параметры
алгоритма оптимизации, значения которых и определяют
конфигурацию алгоритма fminsearch, причем fminsearch
чувствительна к следующим опциям:
options.MaxIter – максимальное количество итераций, значение по
умолчанию – 200*n, где n- количество переменных;
options.MaxFunEvals – максимальное количество оценок функции
затрат, значение по умолчанию – 200*n, где n – количество
переменных;
options.TolFun – абсолютный допуск по значению функции, значение которого по умолчанию – 1.e-4;
options.TolX – абсолютный допуск на размер симплекса, значение по умолчанию – 1.e-4;
options.Display – подробный уровень, для которого возможны значения: "notify","iter","final" или "off", значение по умолчанию –
"notify";
options.OutputFcn – выходная функция или список выходных
функций;
options.PlotFcns – функция печати или список функций печати.
Выходные параметры:
X – значение аргумента, обеспечившее минимальное значение функции;
fval– минимальное значение функции.
еxitflag – флаг, связанный со статусом выполнения алгоритма:
-1 – максимальное количество итераций достигнуто;
0 – максимальное число оценок функций достигнуто;
1 – допуск на размер симплекса и его изменения уже
достигнут: алгоритм не имеет сходимости;
output – структура данных, которая хранит информацию о
выходных данных и содержит следующие поля:
output.algorithm – строка, содержащая название алгоритма, то есть алгоритма Нелдера-Мида;
output.funcCount – количество оценок функции;
output.iterations – количество итераций;
output.message – строка, содержащая сообщение о завершении.
Критерии прекращения процесса оптимизации используют следующие переменные:
s size – текущий размер симплекса;
s hiftfv – абсолютное значение разности значения функции
между самой высокой и самой низкой вершиной.
Процесс итерации останавливается, если выполняются следующие
условия: ssize < options . TolFun&shiftfv < options . TolFun.
Алгоритм, заложенный в fminsearch использует специальный начальный симплекс, который вычисляется эвристически в зависимости от начального предположения (подробнее см. в документации о optimsimplex [ x ]) .
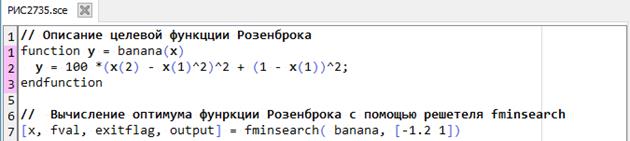
В следующих примерах для вычисления минимума функции Розенброка воспользуемся решателем fminsearch, описав предварительно функцию под именем banana, и задав начальные значения поиска [-1.2 1.0]. В данном случае для поиска минимума потребовалось выполнение 85 итераций и 159 обращений к функции оценки (рис. 2.7.3-5).

--> // Загрузка сценария РИС2735
--> // и вычисление минимума с использованием решателя fminsearch
-->
--> exec('РИС2735.sce', 0)
[output.Output, output.funcCount, output.iterations, output.message]
exitflag =
1.
fval =
0.00000000081776611
x =
1.0000220217835567 1.0000422197517711
--> mprintf('algorithm = %c\nfuncCount = %4d\niterations = %3d',…
output.algorithm, output.funcCount, output.iterations);
algorithm = Nelder-Mead simplex direct search
funcCount = 159
iterations = 85
--> output.message
ans =
!Optimization terminated:
!
! the current x satisfies the termination criteria using OPTIONS.TolX of 0.0001 ! and F(X) satisfies the convergence criteria using OPTIONS.TolFun of 0.0001 !
Рис. 2.7.3-5 Вычисление минимума функции Розенброка
с использованием решателя fminsearch
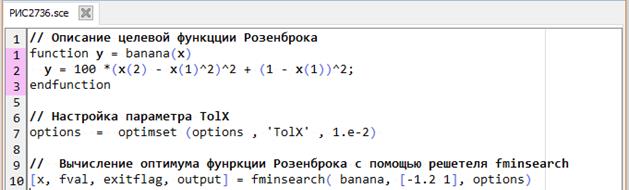
Далее рассмотрим пример вычисление минимума функции Розенброка решателем fminsearch с настраиваемыми опциями. Настроим абсолютный допустимый размер симплекса до большего значения, так чтобы алгоритм выполнял меньшее количество итераций. Поскольку по умолчанию значение t olX=1.e-4, заменим его в optimset на большее значение, например, 1.e-2. В данном случае потребовалось 70итераций и 130обращений к функции оценки (рис. 2.7.3-6).

-->// Загрузка сценария РИС2735, настройка некоторых опций
-->// и вычисление минимума с использованием решателяfminsearch
--> exec('РИС2736.sce', 0)
options =
Display: [0x0 constant]
FunValCheck: [0x0 constant]
MaxFunEvals: [0x0 constant]
MaxIter: [0x0 constant]
OutputFcn: [0x0 constant]
PlotFcns: [0x0 constant]
TolFun: [0x0 constant]
TolX: [1x1 constant]
output =
algorithm: [1x1 string]
funcCount: [1x1 constant]
iterations: [1x1 constant]
message: [3x1 string]
exitflag =
1.
fval =
0.0000085
x =
1.001016 1.0017605
-->
--> mprintf('algorithm = %c\nfuncCount = %4d\niterations = %3d',…
output.algorithm, output.funcCount, output.iterations);
algorithm = Nelder-Mead simplex direct search
funcCount = 130
iterations = 70
-->
--> output.message
ans =
!Optimization terminated: !
! the current x satisfies the termination criteria using OPTIONS.TolX of 0.01
! and F(X) satisfies the convergence criteria using OPTIONS.TolFun of 0.0001
Рис. 2.7.3-6. Вычисление минимума функции Розенброка
решателем fminsearch с настраиваемыми опциями
Решатель nmplot
Кроме описанных выше решателей optim и fminsearch, в Scilab представляет интерес решатель nmplot [13], который использует алгоритмы оптимизации прямого поиска, при этом всю информацию о процессе оптимизации на каждой итерации можно отобразить на экране или сохранить в файлах для ее последующего анализа.
Решатель nmplot включает несколько методов оптимизации прямого поиска, основанных на симплексном методе. Он является модификацией компонента neldermead, с выводом результатов, и позволяет хранить историю значений данных в процессе итераций.
Этими данные могут быть:
· значения координат симплекса;
· значения функции, усредненные по вершинам;
· минимальные значения функции в симплексе;
· размеры симплекса.
Во время процесса оптимизации эти данные хранятся в нескольких файлах.
На рис. 2.7.3-7 приведен пример только графической траектории поиска минимума функции с использованием решателя nmplot. Подробноэтотпримериспользования решателя nmplot рассмотрен в [13]. Из которого следует, что выбор направления спуска определяется симплексом.
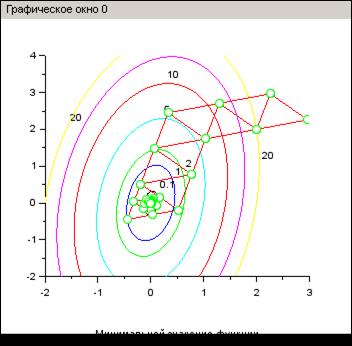
Рис. 2.7.3-7 Траектория спуска при поиске минимума с использованием
решателя nmplot
2.7.4 Контрольные вопросы
1) Как формулируется постановка численного решения задачи оптимизации нелинейных функций?
2) Что является безусловной и условной оптимизацией нелинейных функций?
3) Что является достаточными условиями существования минимума для одномерной и многомерной функции?
4) Что такое локальный и глобальный минимумы функций?
5) Можно ли средствами Scilab вычислить глобальный минимум заданной функции?
6) Какие исследования целевой функции целесообразно произвести перед поиском локального минимума средствами Scilab?
7) Как выбрать начальные приближения в случае многомерной оптимизации?
8) Что такое решатель и в чем его обличие от функции?
9) На каких идеях основаны Квази-Ньютоновские алгоритмы поиска оптимума?
10) На каких идеях основаны методы деформируемого многогранника поиска оптимумам?
11) Какие средства Scilab известны для решения задач оптимизации функций?
12) Какие основные программные средствами оптимизации в Scilab известны?
13) Для чего используется решатель optim?
14) Решатель optim и назначение ее входных и выходных параметров?
15) Для чего при использовании функции optim необходимо формирование вспомогательной функции?
16) Можно ли использовать решатель optim без выходных параметров?
17) Можно ли с использованием решатель optim вычислить локальный максимум?
18) Назначение функции costf , ее входные и выходные параметры.
19) Что служит результатом выполнения решателя optim ?
20) Какие средства Scilab используются для описания целевой функции, и как это влияет на параметры решателя optim ?
21) Для чего используется решатель f minsearch
22) Каковы особенности решателя nmplot?
Приложение
Приложение 1.2
Системные встроенные функции. Таблица 1.2.1-1
| Имя функции | Назначение |
| whos whos() whos -typeТип whos -nameИмя | Отображает переменные в длинной форм е Отображает все текущие имена переменных (без учета регистра), типам и используемой памяти. Отображает все текущие переменные с указанным типом Тип, где Тип – текстовая строка, кодирующая тип данных. Отображает все текущие переменные, имена которых начинаются Имя, где Имя – имена искомых переменных, либо их начальные фрагменты. |
| who who() who('local') who('get') who('global') who('sorted') | Отображает переменные Отображается текущие имена переменных и констант. Отображается имена локальных переменных и параметры память, используемые в данных двойной точности. Отображается имена глобальных переменных и параметры память, используемые в данных двойной точности. Отображается имена всех переменных(если переменная является глобальной, * появляется после имени типа). |
| сlear clear('a',' b ' ,.. ) | Удаление из памяти объектов и освобождение имен переменных Удаляются все незащищенные объекты и освобождаются имена текущей сессии Удаляются указанные незащищенные объекты и освобождаются имена текущей сессии |
| predef() predef('a') predef(' с ') predef('Список') | Защищает переменные Возвращается количество защищенных переменных. Защищаются все переменные из списка who (' get ') . Снимается защита со всех переменных списка who (' get '). Отображается Список защищенных переменных. |
| xists('Имя') exists('Имя', 'l') exists('Имя', 'n') exists('Имя', 'a') | Проверяет существование объекта с указанным им енем Если объект заданного типа существует, то возвращаетсяT, в противном случае F, где' l ' – локальный,' n ' – нелокальный,' a' – все в () (по умолчанию). |
Функции, позволяющие получить номера и названия типов объектов. Таблица 1.2.1-2
| НомерТипаОбъекта = type (O бъект) – Возвращает номер типа объекта. | ||
| НазваниеТипаОбъекта = typeof(O бъект) – Возвращает названия типа объекта. | ||
| № Типа | Название Типа | Примеры |
| 1 | Вещественные или комплексные значения двойной точности (double) | type(42) type(%nan) type(%inf) type(1 + %i) |
| 2 | Полиномиальный (polynomial) | type(1 - %z + %z^2) |
| 4 | Логический (boolean) | type(%t) |
| 8 | Целочисленный (integer): хранятся в 1 (int8), 2 (int16), 4 (int3 2) или 8 (int64) байтах | g = int8([1 - 120127312]) type(g) type(1.23 * int8(4)) |
| 9 | Графические дескрипторы (указатели) | type(gdf()) |
| 10 | Символьный(string) | type("Текст") type('Текст') |
| 13 | Компилированные функции (function) | deff('[y] = f(x)',['a = 3 * x + 1']); type(f) |
| 14 | Библиотеки функций (li b rary) | |
| 15 | Простые списки (list) | l = list(1,["a" "b"]); type(l) |
| 16 | Типизированные списки (tlist) | e = tlist(["lt","f1","f2"], [], []); type(e) |
| 17 | Матрично-ориентированные типизированные списки (mlist) (Структуры,Ячейки, Полиномы,Рациональные дроби) | h=mlist(['V','n','v'],['a','b';'c''d'],[12;34]); type(h) clears,s.r=%pi type(s) // структуры c={%t% pi% i%z"abc "s type(c)} //cell-массивы r=[%z/(1 - %z)(1 - %z) / %z^2] type(r) // рациональныедроби |
| 130 | Встроенные функции (fptr) | type(disp) |
Функции для работы с комплексными данными. Таблица 1.2.2-2
| Функции | Назначение | Примеры |
| complex(a, b) | Создает комплексное число | -->complex(5, 9) ans = 5. + 9.i |
| сonj( a, b) | Создает комплексно-сопряжённое число | -->b = complex(5, 9) b = 5. + 9.i -->conj(b) ans = 5. - 9.i |
| i mag (Z) | Выделяет мнимую часть числа | -->imag(complex(5,9)) ans = 9. |
| real(Z) | Выделяет вещественную часть числа | -->real(complex(5,9)) ans = 5. |
| gcd(V) lcm(V) | Вычисляет наибольший общий делитель и наименьшее общее кратное | --> V = uint16([2^2 * 3^5,… > 2^3 * 3^2, 2^2 * 3^4 * 5]) V = 972 72 1620 -->y = gcd(V) y = 36 --> lcm(V) ans = 9720 |
| atan(imag(Z),real(Z)) atan(imag(Z),real(Z))… *180/% pi | Возвращает фазу угла в радианах Возвращает фазу угла в градусах | -->argZ = atan(imag(1 + %i),… > real(1 + %i)) * 180 / %pi argZ = 45. |
| abs(Z) | Вычисляет модуль комплексного числа. | -->Z = 1 + %i; -->modZ = abs(Z) modZ = 1.4142136 |
| isreal(Z) isreal(a) isreal(b) | Возвращает логическое значение T, если число действительное и F – если комплексное | -->Z = complex(5, 9); -->a = 67.76; -->isreal(b) ans = F -->isreal(Z) ans = F |
Системные константы. Таблица 1.2.2-3
| Системная константа | Назначение | Значения системных констант |
| % i | Мнимая единица | sqrt(-1) |
| % pi | Число π | 3.1415926… |
| % eps | Погрешность числа с плавающей точкой | 2-52 |
| % e | Основание натурального логарифма | 2.71828182 |
| % inf | Значение машинной бесконечности | |
| % nan | Указание на нечисловой характер данных ( Not - a - Number ) | |
| %s %z | Переменные, используемые для определения полиномов | --> z = poly(0, "z"); --> s = poly(0, "s"); |
| ans | Переменная, хранящая результат последней операции |
Функции, определяющие структуру матрицы. Таблица 1.2.2-4
| Функция | Назначение | Пример использования |
| length(М) | Возвращает число элементов в матрице | -->М = [1 2 3;2 3 4;4 5 6]; --> length(M) ans = 9. --> V = [3 4 5 6 7]; --> length(V) ans = 5. |
| length( Y (:, 1)) | Возвращает число строк матрицы | --> X = [1 2;2 3;4 5]; -->length(X(:, 1)) ans = 3. |
| length(X(1, :)) | Возвращает число столбцов матрицы | --> X = [1 2;2 3;4 5]; -->length(М(1, :)) ans = 2. |
| size( М ) [n, m] = size( М ) size(M, 1) size(M, 2) | Возвращает вектор, содержащий количество строк и столбцов матрицы М, или только число строк, или только число столбцов | --> M = [1 3; 2 4; 4 6]; --> size(М) ans = 2. 3. --> [n, m] = size(M) m = 3. n = 2. --> size(M, 1) ans = 2. --> size(M, 2) ans = 3. |
| ndims(T) n = ndims(T) | Возвращает число измерений матрицы | --> T = [2 3 4; 4 3 2; 5 7 8]; --> ndims(T) ans = 2. |
Алгебраические матричные операции и функции. Таблица 1.2.2-5
| Операции и функции | Назначение | Описания |
| + | Сложение | A + B складывает матрицы A и B. |
| + | Унарный плюс | +A возвращает A. |
| - | Вычитание | A - B вычитает B из A. |
| - | Унарный минус | -A меняет знакA . |
| * | Матричное умножение | C = A * B – алгебраическое произведение матриц A и B, при условии, что количество столбцов A равно числу строк B. |
| ^ | Матричное возведение в степень | A^B – возведение матрицы A в степень B, если B является скаляром. Для других значений B вычисления включают собственные значения и собственные вектора. |
| / | Деление матриц слева направо | X = B / A – решение уравнения X * A = B, при условии, что матрицы A и B имеют одинаковое количество столбцов. С точки зрения операций деления слева и транспонирования B / A = (A' \ B')'. |
| \ | Обратное (справа налево) деление матриц | Х = A \ B – решение уравнения A * X = B, при условии, что матрицы A и B имеют одинаковое количество строк. |
| ' | Транспонирование матрицы | B = A' – комплексно-сопряженное транспонирования матрицы A. Для комплексных матриц эта операция не предполагает сопряжения. |
| d = det(mA) | Вычисление определителя матрицы | --> A = [3 2; 4 3]; --> det(A) //Определитель матрицы ans = 1 |
| t = trace(A) | Вычисление следа матрицы, то есть суммы элементов главной диагонали | --> A = [1 2 3; 4 -2 1; 0 3 -1] --> trace(A) //СледматрицыА ans = -2 --> // то же что и --> sum(diag(A)) ans = -2 |
Арифметические поэлементные операции над матрицами. Таблица 1.2.2-6
| Операция | Назначение | Описание |
| + | Сложение | A + B поэлементное сложение A и B |
| + | Унарный плюс | +A возвращает A |
| - | Вычитание | A - B поэлементное вычитание B из A |
| - | Унарный минус | -A поэлементное присвоение в A |
| . * | Поэлементное умножение | C = A .* B поэлементное умножение A и B |
| .^ | Поэлементное возведение в степень | A .^ B поэлементное возведение A в степень B |
| .\ | Поэлементное обратное деление массивов | X = A .\ B – поэлементное обратное деление A и B |
| ./ | Поэлементное деление | X = B ./ A поэлементное деление A и B. |
| .' | Транспонирование массива | A .' – поэлементная операция транспонирования A |
Наиболее часто используемые математические функции. Таблица 1.2.2-7
Дата: 2019-11-01, просмотров: 1013.