Для выполнения оптимизации системы будем использовать следующий компонент, приведенный в таблице 7.
Таблица 7.
Оптимизатор и его реализация
| Элемент | Реализация | Параметры |
| Оптимизатор | 
| 
|
На рис. 19 отражена имитационная модель с оптимизатором, которая соответствует указанной в задании структурной схеме. Параметры модели (постоянная времени, транспортное запаздывание и характеристики регулятора Кп, Ки) соответствуют варианту № 10.

Рис. 19. Имитационная модель заданной системы с оптимизатором
Оптимизация выполняется по интегральному квадратичному критерию качества (ISE). Для оптимизации, в систему добавляется оптимизатор, для которого указывается область допустимых значений ПИ-регулятора (Рис. 20).
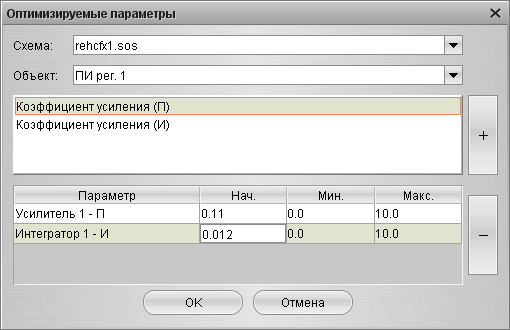
Рис. 20. Заданные настройки оптимизатора
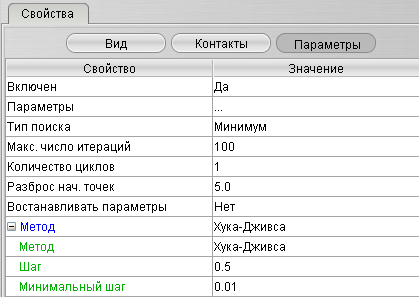
В параметрах оптимизатора был выбран метод Хука-Дживса (Рис.21).

Рис. 21. Параметры оптимизатора
Согласно поставленной задаче, необходимо провести три прогона системы с оптимизатором:
1. YS=0, f=1;
2. YS=1, f=0;
3. YS=1, f=1;
1. Для случая YS=0, f=1 после прогона системы с оптимизатором были получены следующие результаты, представленные на Рис. 22. Таким образом, оптимальные настройки ПИ-регулятора для исходной системы:
Кп = 0,13;
Ки = 0,012 сек-1
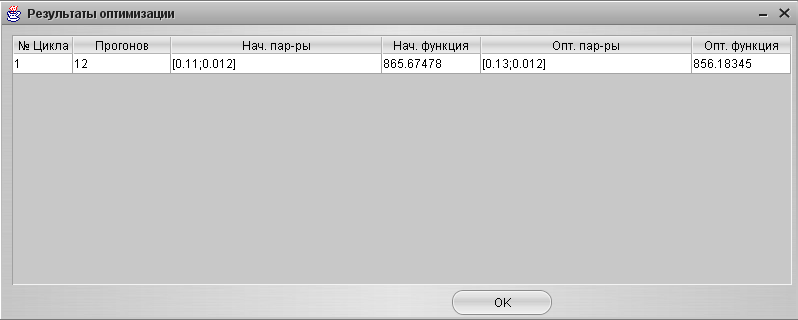
Рис. 22. Результаты оптимизации
Определим показатели качества АСР по переходной характеристике системы (Рис.23).
| hуст |
| А3 |
| А1 |
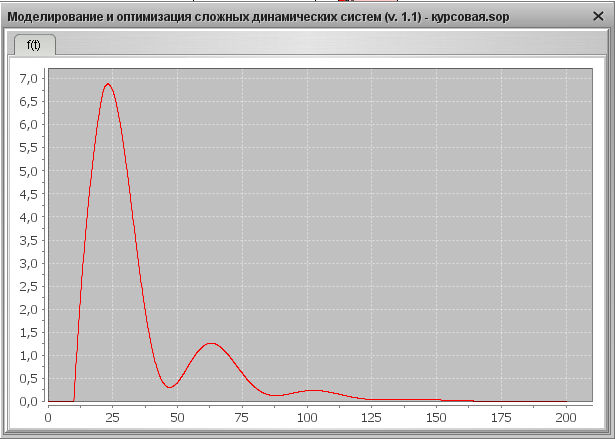
Рис. 23. Переходная характеристика системы YS=0, f=1 после оптимизации
1) Максимальное перерегулирование:
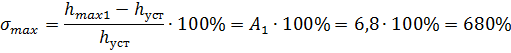
Обычно  .
.
2) Колебательность процесса:
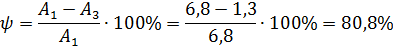
Для работоспособных систем 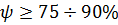
3) Время регулирования в данном случае 115 с.
Качественные характеристики системы представлены в таблице 8.
На основании проведённых расчётов показателей качества можно сделать вывод, что при YS=0, f=1 после оптимизации система неработоспособна в динамике, т.к. не отвечает требованиям.
Таблица 8.
Показатели качества АСР при YS=0, f=1
| Показатель качества | Значение |
Максимальное перерегулирование 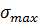
| 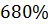
|
Колебательность 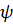
| 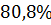
|
| Время регулирования tрегул | 115 с |
2. Для случая YS=1, f=0 после прогона системы с оптимизатором были получены следующие результаты, представленные на Рис. 24. Таким образом, настройки ПИ-регулятора остались неизменны:
Кп = 0,11;
Ки = 0,012 сек-1
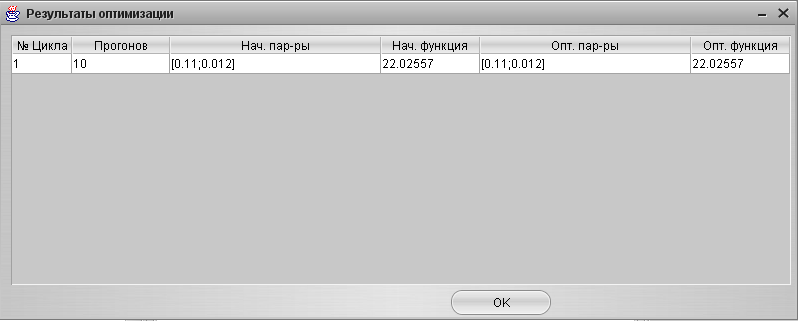
Рис. 24. Результаты оптимизации
Определим показатели качества АСР по переходной характеристике системы (Рис.25).
| А1 |
| А2 |
| hуст |
| А3 |
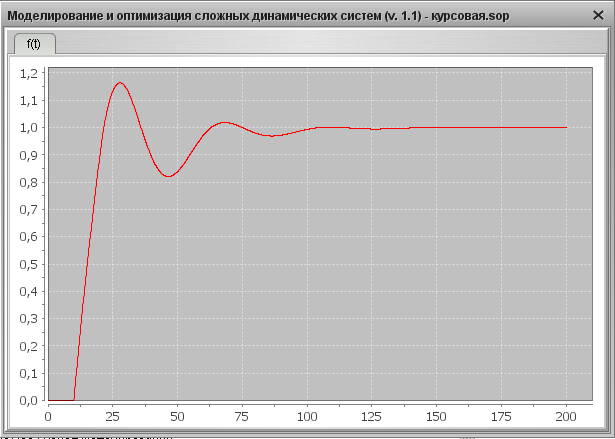
Рис. 25. Переходная характеристика системы YS=1, f=0 после оптимизации
1) Максимальное перерегулирование:
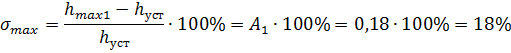
2) Колебательность процесса:
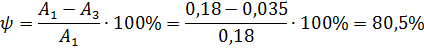
3) Время регулирования в данном случае 95 с.
Качественные характеристики системы представлены в таблице 9.
Таблица 9.
Показатели качества АСР при YS=0, f=1
| Показатель качества | Значение |
Максимальное перерегулирование 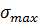
| 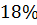
|
Колебательность 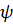
| 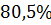
|
| Время регулирования tрегул | 95 с |
На основании проведённых расчётов показателей качества можно сделать вывод, что при YS=1, f=0 после оптимизации система стала работоспособна в динамике, т.к. отвечает требованиям.
2. Для случая YS=1, f=1 после прогона системы с оптимизатором были получены следующие результаты, представленные на Рис. 26. Таким образом, настройки ПИ-регулятора остались неизменны:
Кп = 0,11;
Ки = 0,012 сек-1
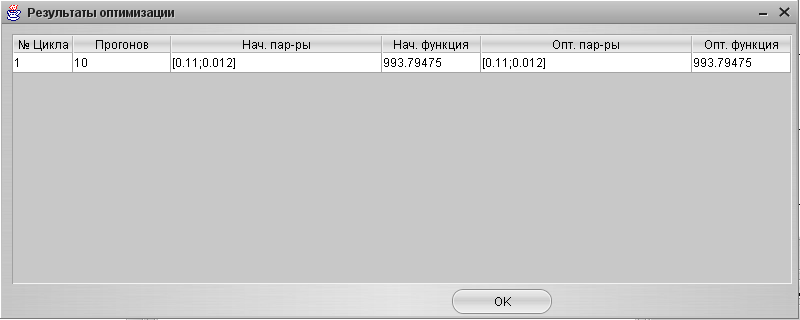
Рис. 26. Результаты оптимизации
Определим показатели качества АСР по переходной характеристике системы (Рис.27).
1) Максимальное перерегулирование:
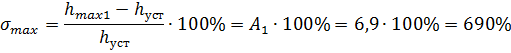
2) Колебательность процесса:

3) Время регулирования в данном случае 113 с.
| А3 |
| А1 |
| hуст |
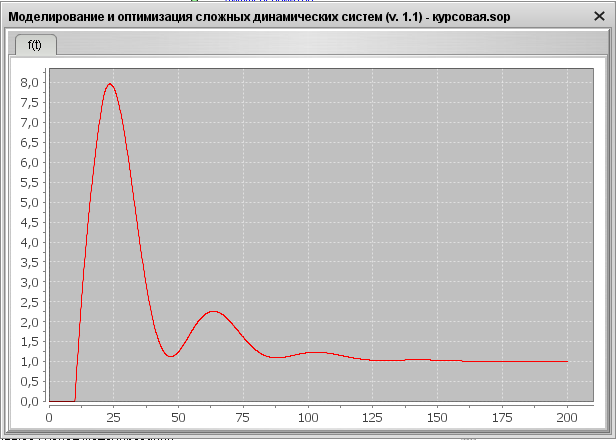
Рис. 27. Переходная характеристика системы YS=1, f=1 после оптимизации
Качественные характеристики системы представлены в таблице 10.
Таблица 10.
Показатели качества АСР при YS=1, f=1
| Показатель качества | Значение |
Максимальное перерегулирование 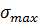
| 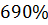
|
Колебательность 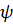
| 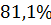
|
| Время регулирования tрегул | 113 с |
На основании проведённых расчётов показателей качества можно сделать вывод, что при YS=1, f=1 после оптимизации система не работоспособна в динамике, т.к. не отвечает требованиям.
Выводы по главе 2
Составим сводную таблицу параметров системы до оптимизации и после (таблица 11).
Таблица 11.
| Критерии качества АСР | До оптимизации | После оптимизации | ||||
| YS=0, f=1 | YS=1, f=0 | YS=1, f=1 | YS=0, f=1 | YS=1, f=0 | YS=1, f=1 | |
Максимальное перерегулирование 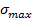
| 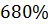
| 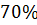
| 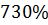
| 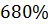
| 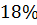
| 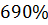
|
Колебательность 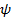
| 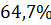
| 
| 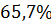
| 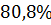
| 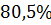
| 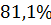
|
| Время регулирования tрегул | 165 с | 170 с | 160 с | 115 с | 95 с | 113 с |
Результаты, полученные с помощью пакета СИМОПТ после оптимизации системы приведены в приложении 2.
Проанализировав таблицу прогона модели до оптимизации и после можно сделать следующие выводы:
1) После проведения оптимизации, показатели качества системы заметно улучшились.
2) В случае YS=1, f=0 (после оптимизации) система стала работоспособна, т.к. удовлетворяет требованиям к показателям качества для работоспособных систем.
3) В случае YS=0, f=1 (после оптимизации) перерегулирование составило 680%, что не удовлетворяет требованиям к показателям качества. Вероятно, это обуславливается исходными параметрами объекта.
4) В случае YS=1, f=1 (после оптимизации) перерегулирование составило 690%, что не удовлетворяет требованиям к показателям качества. Вероятно, это также обуславливается исходными параметрами объекта (инерционного звена первого порядка).
Дата: 2019-07-30, просмотров: 372.