Введение
Моделирование является важнейшим средством анализа и синтеза сложных систем, к которым с полным основанием следует отнести автоматизированные и автоматические системы управления.
Постоянное ужесточение требований к проектам, чрезвычайно высокая цена ошибочных проектных решений и сложность современных объектов проектирования, особенно систем автоматического управления (САУ), входят в противоречие с традиционными инструментами и технологиями проектирования. Выходом из положения является разработка и внедрение нового инструментария проектировщика – системы автоматизации проектирования.
Умение применять инструменты основывается на понимании того, каким образом строится система моделирования, ее структура и отдельные подсистемы, и на знании математических моделей, методов и алгоритмов, которые положены в основу подсистем системы моделирования.
Существующие и проектируемые системы можно эффективно исследовать с помощью математических моделей (аналитических и имитационных), реализуемых на современных ЭВМ, которые в этом случае выступают в качестве инструмента экспериментатора. Такой эксперимент для инженера есть инструмент непосредственного решения организационно-технических задач.
Математическое моделирование динамики САУ позволяет значительно уменьшить объемы макетных испытаний и осуществить:
· анализ функционирования САУ, их устройств и элементов;
· исследование влияния изменения параметров и возмущающих воздействий на стабильность характеристик САУ;
· выбор структурной схемы САУ по задаваемым критериям;
· оценку устойчивости, динамических и статических ошибок для различных значений параметров выбранной структурной схемы и возмущающих воздействии.
Достаточно трудно указать область человеческой деятельности, где не применялось бы моделирование. В настоящее время большое внимание уделяется задачам оценки характеристик сложных систем на основе имитационных моделей.
Объект исследования данной работы – система автоматического управления, состоящая из ПИ-регулятора и инерционного объекта с запаздыванием.
Предмет исследования – динамические свойства заданной САУ.
Целью данной работы является анализ и оптимизация динамических свойств САУ программным методом и с помощью системы имитационного моделирования СИМОПТ.
Структура работы обусловлена предметом, целью и задачами исследования. Работа состоит из введения, 3 глав, заключения.
Введение раскрывает актуальность, определяет объект, предмет, цель и задачи исследования.
В первой главе рассматриваются основные понятия и определения теории автоматического управления, основные понятия и определения моделирования динамических систем, в том числе численные методы решения обыкновенных дифференциальных уравнений (метод Эйлера, метод Рунге-Кутта 4-го порядка, метод трапеций). Приведено описание системы имитационного моделирования СИМОПТ, ее архитектуры и рабочего пространства.
Во второй главе представлена практическая часть работы, выполненная в системе СИМОПТ. Описан порядок сборки имитационной модели, задания параметров системы, процесса прогона модели. Рассчитаны качественные характеристики автоматической системы управления (АСР) до и после оптимизации модели.
В третьем разделе представлена программная реализация отдельных компонентов системы, блок-схема реализации процесса моделирования, рассчитаны качественные характеристики прогона программной модели.
В заключении подводятся итоги исследования, формируются окончательные выводы.
Работа содержит 4 приложения, где приведен листинг разработанной программы и результаты работы программы.
Задание на курсовую работу
Дана структурная схема объекта управления (Рис.1).
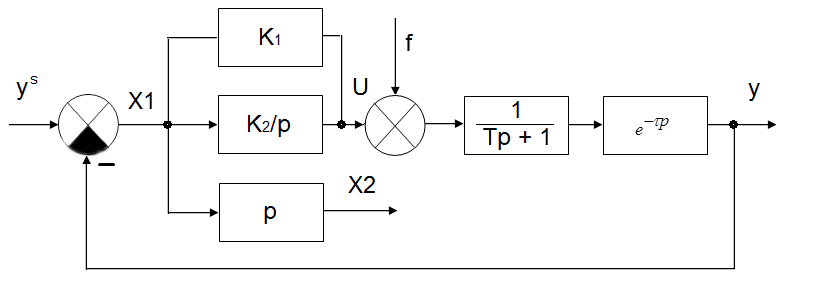
Рис. 1. Структурная схема исходной САУ
САУ состоит из инерционного звена 1 порядка и звена запаздывания. Согласно варианту заданы параметры системы в Таблице 1.
Таблица 1.
Параметры САУ
| № варианта | k | Т | к1 | к2 |
|
| ||||
| 10 | 10 | 0,11 | 0,012 | |
Задачи работы:
1. Выполнить программную реализацию имитационной модели системы управления в заданных режимах работы, состоящей из ПИ-регулятора и инерционного объекта с запаздыванием.
2. В качестве результата вывести фазовый портрет и графики переходного процесса при единичном воздействии (с использованием графической подсистемы Excel).
3. Реализовать прогон модели на системе имитационного моделирования СИМОПТ для двух указанных случаев.
4. Выполнить оптимизацию параметров модели в СИМОПТ. Представить результаты оптимизации.
5. Представить в качестве результатов оптимизации графики переходных процессов и фазовые характеристики при нулевом и единичном воздействии.
6. Оценить параметры системы до и после оптимизации.
Имитационное моделирование проводить для случаев:
1) f=0, YS=1;
2) f=1, YS=0;
Примечание:
1) постоянные времени объекта, транспортное запаздывание и характеристики регулятора k1, k2 выбираются из таблицы 1 (согласно варианту по списку группы) или рассчитываются по методике ;
2) для реализации программной модели инерционного звена используется метод Эйлера.
I. Теоретическая часть
Типовые звенья САР
Звено системы регулирования – элемент, обладающий определенными свойствами в динамическом отношении. Звенья систем регулирования могут иметь разную физическую основу (электрические, пневматические, механические и др. звенья), но относится к одной группе. Соотношение входных и выходных сигналов в звеньях одной группы описываются одинаковыми передаточными функциями.
Простейшие типовые звенья:
1. Усилительное звено (пропорциональное звено) усиливает входной сигнал в К раз. Уравнение звена 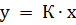 , передаточная функция
, передаточная функция 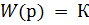 . Усилительное звено является безинерционным звеном.
. Усилительное звено является безинерционным звеном.
2. Идеальное интегрирующее звено имеет выходную величину пропорциональную интегралу входной величины. При подаче сигнала на вход звена выходной сигнал постоянно возрастает. Уравнение звена 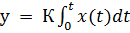 , передаточная функция
, передаточная функция 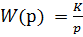 . Идеальное интегрирующее звено является астатическим, т.к. не имеет установившегося режима.
. Идеальное интегрирующее звено является астатическим, т.к. не имеет установившегося режима.
3. Реальное интегрирующее звено имеет передаточную функцию  . Реальное интегрирующее звено является звеном с запаздыванием. Переходная характеристика в отличие от идеального звена является кривой.
. Реальное интегрирующее звено является звеном с запаздыванием. Переходная характеристика в отличие от идеального звена является кривой.
4. Идеальные дифференцирующие звенья физически не реализуемы. Реальные дифференцирующие звенья представляют собой дифференцирующие звенья большинства объектов. Переходная характеристика 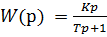 .
.
5. Апериодическое (инерционное) звено первого порядка. Переходная характеристика 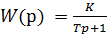 .
.
6. Колебательное звено. При подаче на вход ступенчатого воздействия амплитудой  переходная кривая будет иметь один из двух видов: апериодический (при
переходная кривая будет иметь один из двух видов: апериодический (при 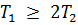 ) или колебательный (при
) или колебательный (при  ). Переходная характеристика
). Переходная характеристика 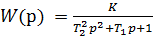 .
.
7. Запаздывающее звено. Передаточная функция звена: 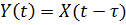 или
или 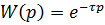 . Выходная величина
. Выходная величина 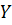 повторяет входную величину
повторяет входную величину 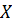 с некоторым запаздыванием
с некоторым запаздыванием 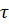 .
.
Качество САР
В общем случае качество регулирования представляет собой совокупность точности в установившемся режиме и качества переходных процессов.
Оценки качества могут быть прямыми и косвенными. В свою очередь прямые и косвенные могут быть статическими и динамическими. Динамические оценки характеризуют переходной процесс, а статические - установившийся режим.
Качество любой системы регулирования определяется величиной ошибки (1.1.13).
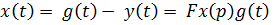 (1.1.13)
(1.1.13)
Однако функцию ошибки x(t) для любого момента времени трудно определить, поскольку она описывается с помощью ДУ высокого порядка, и зависит от большого количества параметров системы. Поэтому оценивают качество САР по некоторым ее свойствам, которые с помощью критериев качества.
Критерии качества регулирования разделяют на 4 группы:
1) Критерии точности – используют величину ошибки в различных типовых режимах.
2) Критерии величины запаса устойчивости – оценивают удаленность САР от границы устойчивости.
3) Критерии быстродействия – оценивают быстроту реагирования САР на появление задающего и возмущающего воздействий.
4) Интегральные критерии – оценивают обобщенные свойства САР: точность, запас устойчивости, быстродействие.
Оценка запаса устойчивости и быстродействия во временной области производится по переходной характеристике при типовом входном или возмущающем воздействии – единичном скачке (Рис. 6).
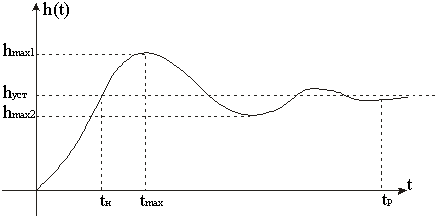
Рис. 6. Переходная характеристика
Если переходная характеристика представляет собой затухающие колебания, то система считается устойчивой. При этом допускается не более 2-3 колебаний.
К основным прямым оценкам относятся следующие: s -регулирование, tp- время регулирования, e - декремент затухания, w - частота колебаний, n - число колебаний, которое имеет переходная характеристика за время регулирования tp, tH - время нарастания переходного процесса, tmax - время достижения первого максимума.
Перерегулирование есть разность между максимальным значением hmax1 переходной характеристики и её установившимся значением, выраженная в процентах (1.1.14).
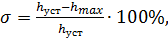 (1.1.14)
(1.1.14)
В большинстве случаев требуется, чтобы перерегулирование не превышало 20 – 30%,
Время регулирования оценивает длительность переходного процесса. За время регулирования принимается тот интервал времени, по истечении которого отклонение переходной характеристики от установившегося значения не превышает некоторой заданной величины q. Значение q выбирают обычно равным 5%.
При заданных значениях s и tp переходная характеристика не должна выходить из определенной области, которая называется областью допустимых отклонений.
В статическом режиме САР оценивается коэффициентом статизма (астатизма) (1.1.15).
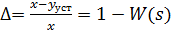 , (1.1.15)
, (1.1.15)
где x – задание; yуст - установившееся значение рабочего параметра.
Рассмотренные выше оценки качества относятся к прямым. Вместе с тем существуют косвенные, среди которых наибольшее распространение получили интегральные оценки. Существует две разновидности интегральной оценки: линейная и квадратичная. Численно линейная интегральная оценка равна площади, ограниченной кривой ошибки или разности 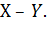 Значение Y берется в пределах временного интервала от 0 до tp. Линейная интегральная оценка определяется следующим выражением (1.1.16).
Значение Y берется в пределах временного интервала от 0 до tp. Линейная интегральная оценка определяется следующим выражением (1.1.16).
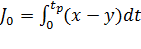 (1.1.16)
(1.1.16)
Эта оценка может быть применена только при монотонных переходных процессах при отсутствии колебаний.
Квадратичная интегральная оценка применяется как при монотонных, так и при колебательных переходных процессах и определяется следующим соотношением (1.1.17).
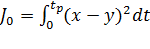 (1.1.17)
(1.1.17)
Недостаток квадратичной интегральной оценки заключается в том, что различные по характеру переходные процессы могут иметь одну и ту же величину оценки. Пример показан на Рис. 7.
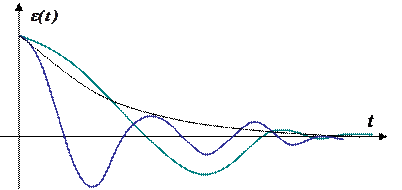
Рис. 7. Типы переходных процессов с одним значением квадратичной интегральной оценки
Выводы по разделу
Совокупность математических описаний элементов системы даёт математическую модель автоматической системы. Математические модели описывают элементы и системы автоматического регулирования в двух режимах: установившемся – статике и переходном – динамике. В рамках данной работы целесообразно рассмотреть элементы САР в динамическом режиме.
Качество регулирования представляет собой совокупность точности в установившемся режиме и качества переходных процессов.
Оценки качества могут быть прямыми (перерегулирование, колебательность, статическая ошибка) и косвенными (линейная и квадратичная интегральная оценка).
Метод Эйлера
Метод Эйлера является простейшим методом интегрирования. Его суть заключается в том, что по известной производной 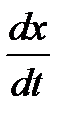 в момент времени
в момент времени 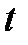 рассчитывается значение функции
рассчитывается значение функции 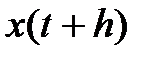 , где
, где 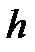 – шаг интегрирования (1.2.11).
– шаг интегрирования (1.2.11).
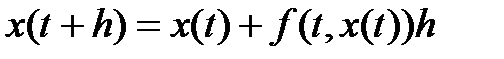 . (1.2.11)
. (1.2.11)
Геометрической интерпретацией метода Эйлера является построение ломаной прямой искомой функции (рис. 8).
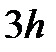
|

|
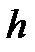
|
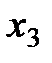
|
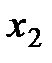
|
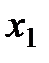
|
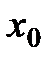
|
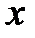
|
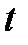
|
Рис. 8. Геометрическая интерпретация метода Эйлера
Метод Эйлера – единственный метод, который позволяет заранее (за шаг) рассчитать значение искомой функции, но он обладает самой большой ошибкой 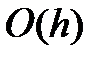 - первый порядок ошибки.
- первый порядок ошибки.
Метод трапеций (метод Хьюна)
Метод трапеций является модификацией метода Эйлера и использует 2 значения входной функции для расчета интеграла. Итерационная формула метода выглядит так (1.2.12).
 . (1.2.12)
. (1.2.12)
Метод трапеций обладает ошибкой второго порядка - 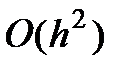 .
.
Оптимизация
Оптимизация динамических систем является важной частью моделирующих программ, и ее реализация позволяет значительно увеличить полезность разрабатываемого инструментария.
Оптимизация динамической системы подразумевает нахождение таких ее параметров, которые минимизируют (максимизируют) определенные динамические свойства или характеристики системы. Примером оптимизации динамической системы является нахождение оптимальных настроек регулятора САР, которые позволяют достигнуть наилучшего качества переходного процесса (перерегулирование, время регулирования и т. д.)
Возможны два подхода к решению задачи отыскания минимума функции многих переменных 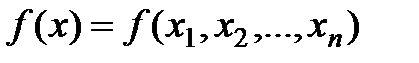 при отсутствии ограничений на диапазон изменения неизвестных.
при отсутствии ограничений на диапазон изменения неизвестных.
Первый подход лежит в основе косвенных методов оптимизации и сводит решение задачи оптимизации к решению системы нелинейных уравнений, являющихся следствием условий экстремума функции многих переменных.
Решение систем нелинейных уравнений - задача весьма сложная и трудоемкая. Вследствие этого на практике используют второй подход к минимизации функций, составляющий основу прямых методов. Суть их состоит в построении последовательности векторов 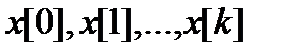 , таких, что
, таких, что 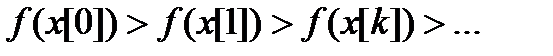 . В качестве начальной точки
. В качестве начальной точки  может быть выбрана произвольная точка, однако стремятся использовать всю имеющуюся информацию о поведении функции
может быть выбрана произвольная точка, однако стремятся использовать всю имеющуюся информацию о поведении функции  , чтобы точка
, чтобы точка  располагалась как можно ближе к точке минимума. Переход (итерация) от точки
располагалась как можно ближе к точке минимума. Переход (итерация) от точки 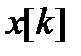 к точке
к точке 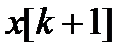 ,
, 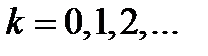 , состоит из двух этапов:
, состоит из двух этапов:
1) выбор направления движения из точки 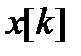 ;
;
2) определение шага вдоль этого направления.
Методы построения таких последовательностей часто называют методами спуска, так как осуществляется переход от больших значений функций к меньшим значениям.
Математически методы спуска описываются соотношением (1.2.14).
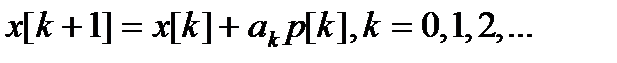 (1.2.14)
(1.2.14)
где 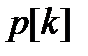 - вектор, определяющий направление спуска;
- вектор, определяющий направление спуска; 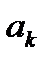 - длина шага.
- длина шага.
Различные методы спуска отличаются друг от друга способами выбора двух параметров - направления спуска и длины шага вдоль этого направления. На практике применяются только методы, обладающие сходимостью. Они позволяют за конечное число шагов получить точку минимума или подойти к точке, достаточно близкой к точке минимума. Качество сходящихся итерационных методов оценивают по скорости сходимости.
Для организации подсистемы оптимизации в разрабатываемой системе необходимо выбрать методы для реализации, исходя из типа решаемой задачи и качества метода. Специфика оптимизации динамических систем, заданных структурными схемами и неявность задания целевой функции, значение которой может быть рассчитано только после проведения моделирования всей системы в целом обуславливают использования методов нулевого порядка.
Рассмотрим один из методов оптимизации нулевого порядка: метод Хука-Дживса. Выбор данного метода обусловлен: хорошей алгоритмизацией, легкостью реализации; удобством модификации метода для реализации условной оптимизации; наличием тестовых примеров для отладки.
Метод Хука-Дживса
Суть этого метода состоит в следующем. Задаются некоторой начальной точкой  . Изменяя компоненты вектора
. Изменяя компоненты вектора  , обследуют окрестность данной точки, в результате чего находят направление, в котором происходит уменьшение минимизируемой функции
, обследуют окрестность данной точки, в результате чего находят направление, в котором происходит уменьшение минимизируемой функции  . В выбранном направлении осуществляют спуск до тех пор, пока значение функции уменьшается. После того как в данном направлении не удается найти точку с меньшим значением функции, уменьшают величину шага спуска. Если последовательные дробления шага не приводят к уменьшению функции, от выбранного направления спуска отказываются и осуществляют новое обследование окрестности и т. д.
. В выбранном направлении осуществляют спуск до тех пор, пока значение функции уменьшается. После того как в данном направлении не удается найти точку с меньшим значением функции, уменьшают величину шага спуска. Если последовательные дробления шага не приводят к уменьшению функции, от выбранного направления спуска отказываются и осуществляют новое обследование окрестности и т. д.
Исходными данными для работы метода являются:
1)  – вектор начальных значений;
– вектор начальных значений;
2) d – начальный шаг поиска;
3) 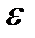 – минимальный шаг поиска.
– минимальный шаг поиска.
Ниже представлена блок-схема алгоритма метода Хука-Дживса.
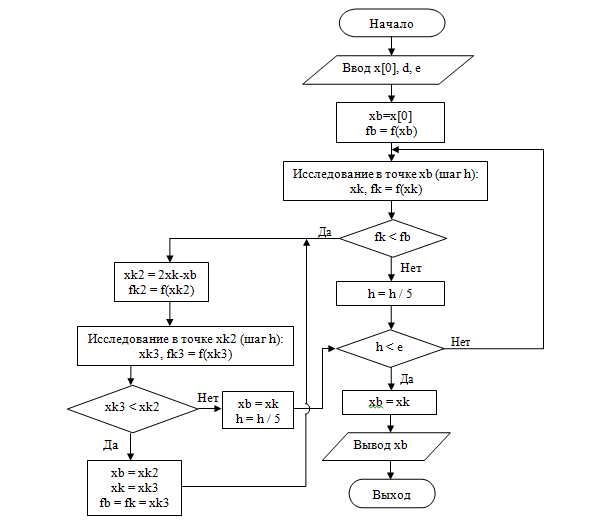
Рис.9 Блок-схема алгоритма метода Хука-Дживса
Заметим, что величина уменьшение шага в 5 раз выбрана экспериментальным путем, ее изменение может привести к увеличению или уменьшению скорости сходимости метода в зависимости от решаемой задачи.
Выводы по разделу
При математическом моделировании в качестве объекта моделирования выступают исходные уравнения, представляющие математическую модель объекта, а в качестве модели системы выступают процессы, которые воспроизводятся на ЭВМ и решают по заданным уравнениям поведение отдельных компонент и их взаимосвязь в системе.
Пропорционально – интегральный регулятор можно представить как последовательное соединение безинерционного, интегрирующего и пропорционально – дифференцирующего звеньев. Выбор обусловлен тем, что ПИ-регулятор улучшает статику и динамику системы. Пропорциональная составляющая увеличивает быстродействие системы, но приводит к статической ошибке. Интегральная составляющая ПИ-регулятора снижает быстродействие системы, но убирает статическую ошибку.
Метод Эйлера является простейшим методом интегрирования, однако это единственный метод, который позволяет заранее (за шаг) рассчитать значение искомой функции.
Оптимизация динамических систем является важной частью моделирующих программ, и ее реализация позволяет значительно увеличить полезность разрабатываемого инструментария.
Метод оптимизации Хука-Дживса имеет следующие характеристики: хорошей алгоритмизацией, легкостью реализации; удобством модификации метода для реализации условной оптимизации; наличием тестовых примеров для отладки.
СИМОПТ
Математическое ядро
Основной функцией математического ядра является формирование потока исполнения модели на основе ее структурной схемы. Под потоком исполнения понимается порядок вызова вычислительных процедур блоков модели.
При формировании единого потока выполнения встает ряд трудностей, связанных с:
· Наличием составных элементов (ГЭС);
· Наличием разветвителей сигналов (три графические связи относятся к одному и тому же сигналу);
· Наличием нескольких структурных схем одной модели, сигналы между которыми передаются по специальным блокам;
· Наличие циклов (обратные связи).
Проблема циклов разрешается благодаря так называемым блокам с эффектом памяти. К данным блокам относятся интегратор, звено запаздывания, апериодическое звено 1-ого порядка и т.д. Относительно данных блоков действует закон, на данном шаге выходное значение блока не зависит от его входного значения (действительно только при интегрировании по Эйлеру без использования итерационного решателя). Таким образом данные блоки участвуют в потоке исполнения модели дважды: один раз как генераторы сигнала, а второй раз как приемники сигнала.
Принцип решения первых трех трудностей, связан с требованием, чтобы результирующий поток исполнения не содержал не разветвителей, ни портов ГЭС, ни передающих сигналов блоков. То есть из системы на основе связей изымаются данные блоки и происходит переход от графических связей к сигналам. Каждый сигнал имеет уникальный идентификатор. Для реализации данного перехода используется рекурсивный алгоритм. Результат работы подобного алгоритма показан на рис. 13.
| 4 |
| 2 |
| 5 |
| 5 |
| 3 |
| 1 |
| 2 |
| y(t) |
|
|

| g(t) |
Рис. 13 Результирующая схема с сигналами
Одновременно при работе рекурсивного алгоритма определяется список блоков генераторов сигнала на основе информации о готовности их выходных сигналов (всегда готовы для выдачи). Данные блоки первыми попадают в итоговый поток исполнения.
Затем для каждого генераторного блока по карте схемы находятся блоки приемники сигнала. Если они готовы для расчета, то они также заносятся в поток и сами попадают в конец списка генераторных блоков. Таким образом все блоки заносятся в результирующий поток причем дважды в него попадают только генераторные блоки.
Выводы по разделу
Современные программные средства по моделированию систем различных классов поддерживают принцип визуального моделирования.
Пакеты визуального моделирования позволяют пользователю вводить описание моделируемой системы в естественной для прикладной области и преимущественно графической форме (например, ввод функциональной схемы), а также представлять результаты моделирования в наглядной форме, например, в виде диаграмм или анимационных картинок.
Для дальнейшего эффективного использования программы были приведены диаграмма реализации системы СИМОПТ, описаны архитектура, функциональные возможности, рабочее пространство системы, подсистема представления результатов, математическое ядро и система помощи.
Выводы по главе 1
В первой части главы 1 приведено описание основных понятий и определений теории автоматического управления, способы вычисления динамических показателей качества для системы автоматического регулирования, а также представлены интегральные критерии качества, применяемые для анализа и синтеза систем при имитационном моделировании.
Во второй части приведена характеристика моделирования систем автоматического управления, промышленных регуляторов, объектов управления. Изложены основные методы моделирования, в том числе и метод Эйлера для решения дифференциальных уравнений первого порядка. Рассмотрено понятие оптимизации САУ, в частности метод Хука-Дживса.
В третьей части главы 1 приводится подробное описание пакета СИМОПТ, которое необходимо для реализации модели в данной системе.
На основе вышеперечисленных понятий и методов будет создана программная реализация имитационной модели системы.
Оценка параметров системы
Установим шаг моделирования h=0,1 и время моделирования T=200 с.
После окончания моделирования получим значения. Снятие графиков с системы осуществляется двойным щелчком левой кнопкой мыши на компонентах «График f(t)» и «График y(x)».
Нам необходимо рассмотреть несколько вариантов условий, в которых будет работать система. Для начала примем задающее воздействие равное нулю (YS = 0), а на вход объекта управления подадим возмущение в виде «единичной ступеньки» (f = 1). Затем, наоборот, возмущение будет равно 0, а задающее воздействие 1(YS = 1; f = 0). Для третьего случая (YS = 1; f = 1) необходимо будет задать 1 в параметрах ступенек в системе СИМОПТ. Таким образом, согласно поставленной задаче, необходимо провести три прогона системы:
1. YS=0, f=1;
2. YS=1, f=0;
3. YS=1, f=1;
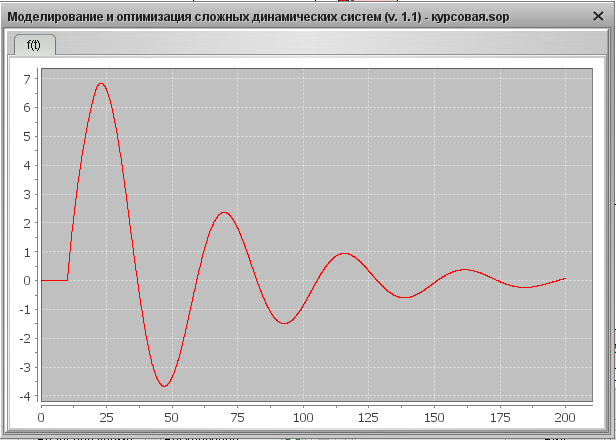
1. Определим показатели качества АСР для случая YS=0, f=1: время регулирования tp, перерегулирование s, колебательность y. Для этого используем переходную характеристику системы, представленную на Рис. 16.
1) Максимальное перерегулирование – максимальное отклонение переходной характеристики от установившегося значения переходной величины, выраженное в относительных единицах.
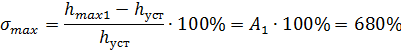
Обычно  .
.
| hуст |
| А4 |
| А3 |
| А1 |
| А2 |
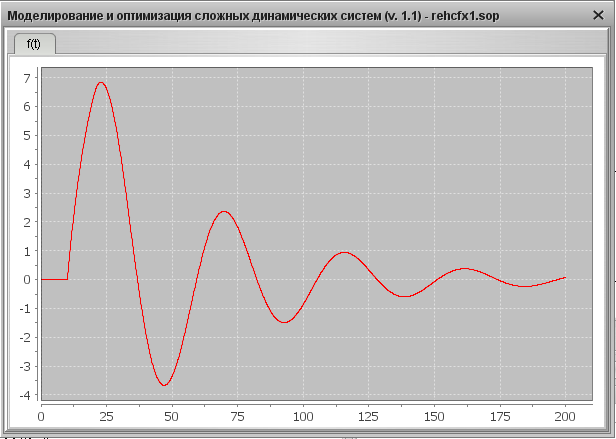
Рис. 16. Переходная характеристика на выходе системы при YS=0, f=1
2) Колебательность процесса
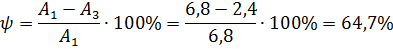
(определяется как отношение разности двух соседних амплитуд, направленных в одну сторону, к большей из них в относительных единицах).
Для работоспособных систем 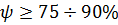
3) Время регулирования – tрегул - минимальное время от начала нанесения возмущения до момента, когда регулируемая величина будет оставаться близкой к установившемуся значению с заданной точностью, т.е. 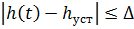 , где Δ – постоянная величина, значение которой нужно оговаривать (обычно Δ=2
, где Δ – постоянная величина, значение которой нужно оговаривать (обычно Δ=2 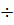 5% hуст). В данном случае время регулирования 165 с.
5% hуст). В данном случае время регулирования 165 с.
Качественные характеристики системы представлены в таблице 4.
Таблица 4.
Показатели качества АСР при YS=0, f=1
| Показатель качества | Значение |
Максимальное перерегулирование 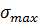
| 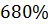
|
Колебательность 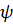
| 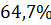
|
| Время регулирования tрегул | 165 с |
На основании проведённых расчётов показателей качества можно сделать вывод, что при YS=0, f=1 система неработоспособна в динамике, т.к. не отвечает требованиям.
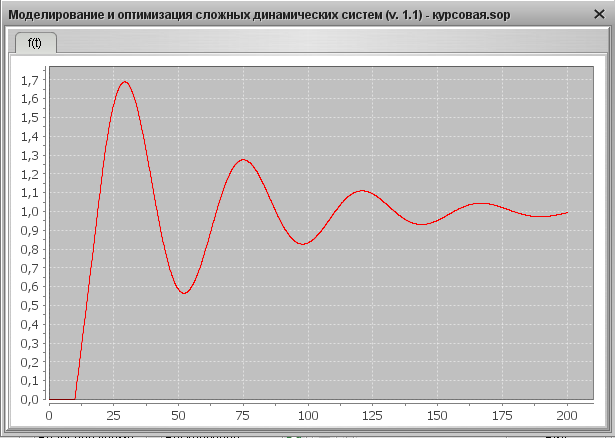
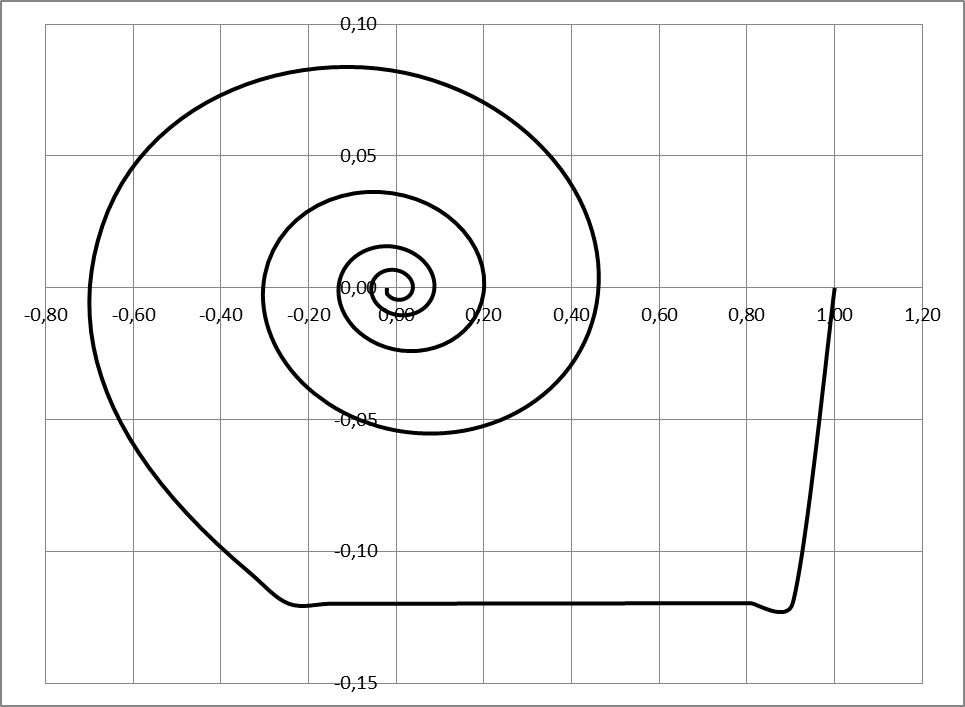
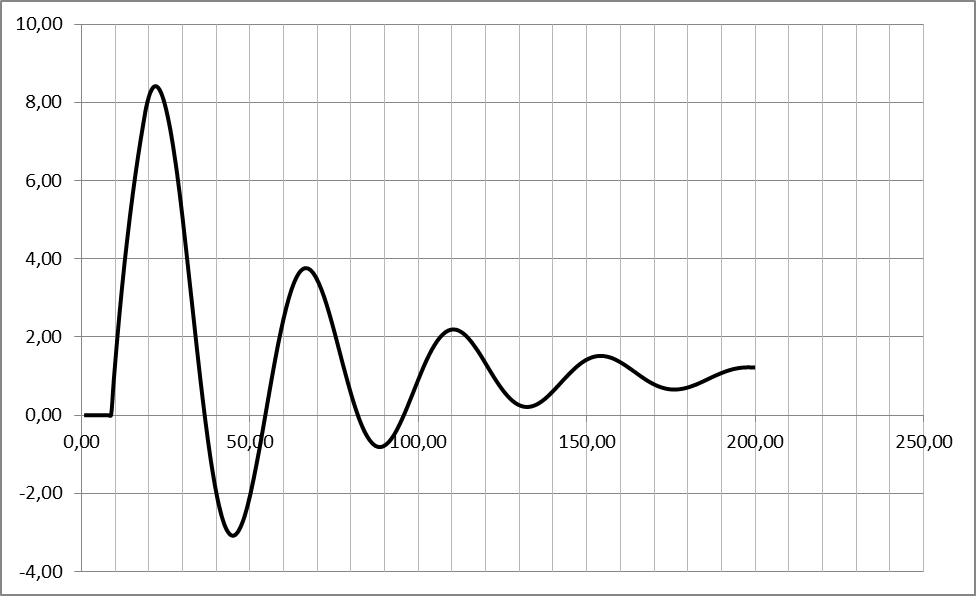
2. Определим показатели качества АСР для случая YS=1, f=0: время регулирования tp, перерегулирование s, колебательность y. Для этого используем переходную характеристику системы, представленную на Рис. 17.
| hуст |
| А3 |
| А4 |
| А2 |
| А1 |
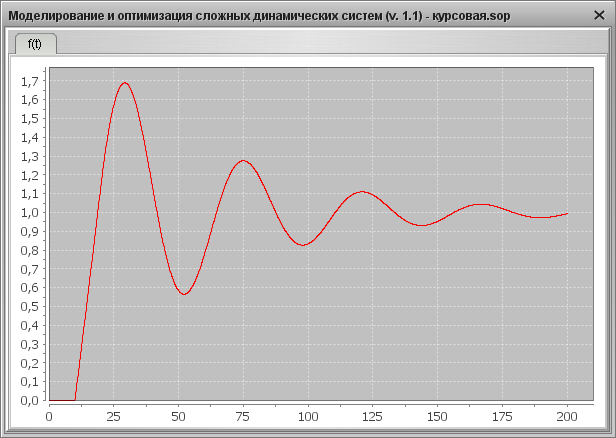
Рис. 17. Переходная характеристика на выходе системы при YS=1, f=0
1) Максимальное перерегулирование:
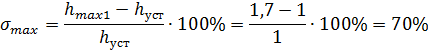
2) Колебательность процесса:
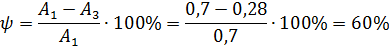
3) Время регулирования в данном случае 170 с.
Качественные характеристики системы представлены в таблице 5.
Таблица 5.
Показатели качества АСР при YS=1, f=0
| Показатель качества | Значение |
Максимальное перерегулирование 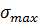
| 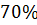
|
Колебательность 
| 
|
| Время регулирования tрегул | 170 с |
На основании проведённых расчётов показателей качества можно сделать вывод, что при YS=1, f=0 система неработоспособна в динамике, т.к. не отвечает требованиям.
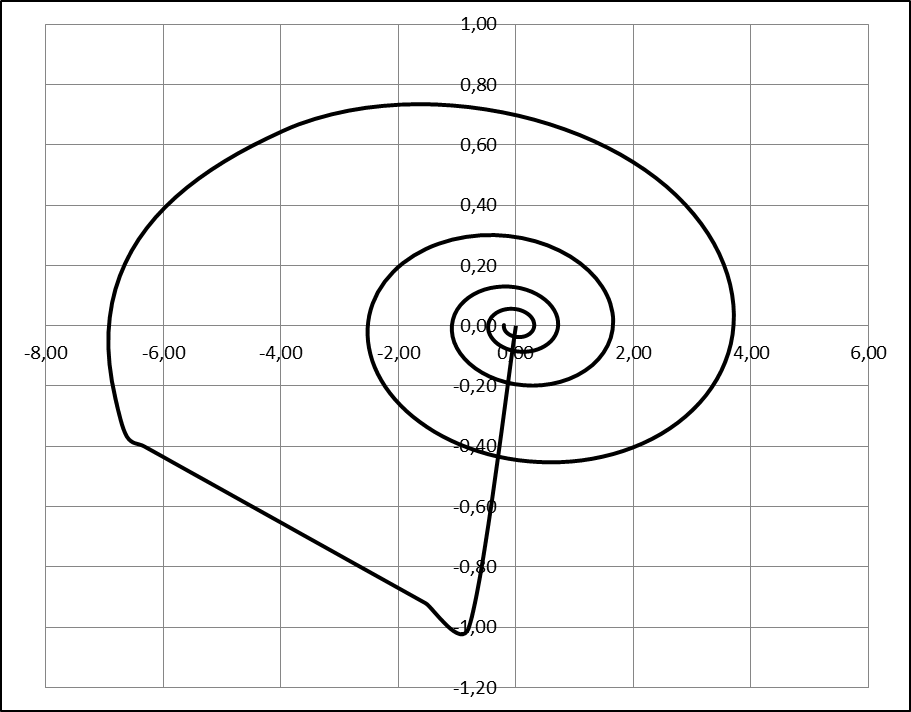
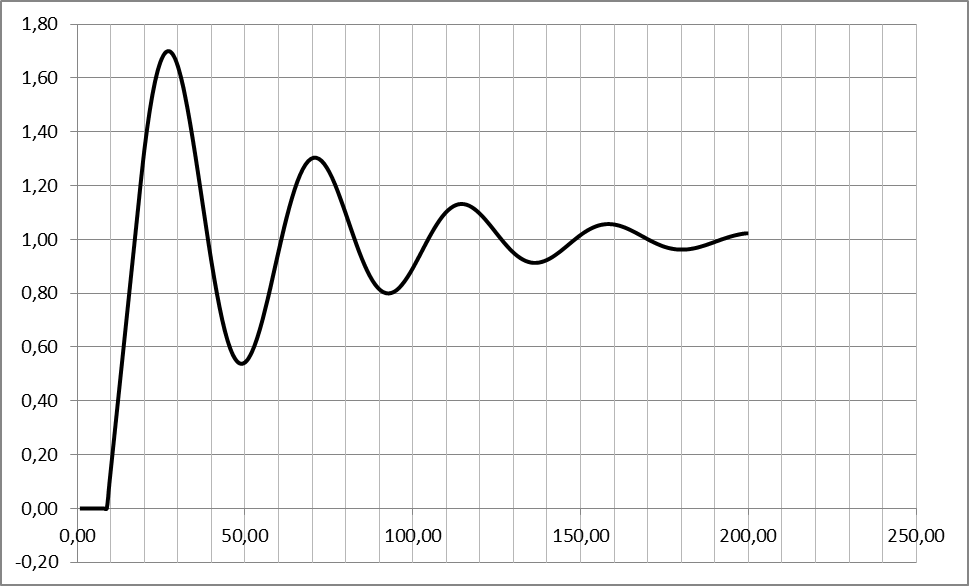
3. Определим показатели качества АСР для случая YS=1, f=1: время регулирования tp, перерегулирование s, колебательность y. Для этого используем переходную характеристику системы, представленную на Рис. 18.
| hуст |
| А4 |
| А2 |
| А3 |
| А1 |
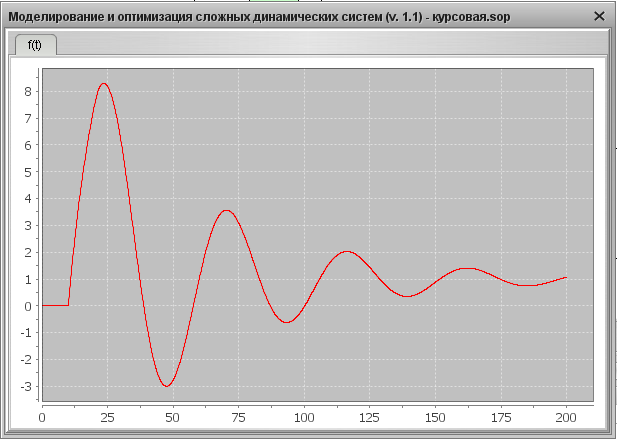
Рис. 18. Переходная характеристика на выходе системы при YS=1, f=1
1) Максимальное перерегулирование:
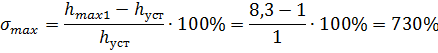
2) Колебательность процесса:
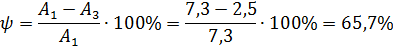
3) Время регулирования в данном случае 160 с.
Качественные характеристики системы представлены в таблице 6.
Таблица 6.
Показатели качества АСР при YS=1, f=1
| Показатель качества | Значение |
Максимальное перерегулирование 
| 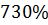
|
Колебательность 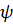
| 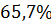
|
| Время регулирования tрегул | 160 с |
На основании проведённых расчётов показателей качества можно сделать вывод, что при YS=1, f=1 система неработоспособна в динамике, т.к. не отвечает требованиям.
Из вышеперечисленных расчетов можно сделать вывод о неработоспособности и неэффективности данной системы во всех трех случаях. Для улучшения показателей требуется оптимизация параметров системы. Результаты, полученные с помощью пакета СИМОПТ до оптимизации системы приведены в Приложении 1.
Выводы по главе 2
Составим сводную таблицу параметров системы до оптимизации и после (таблица 11).
Таблица 11.
| Критерии качества АСР | До оптимизации | После оптимизации | ||||
| YS=0, f=1 | YS=1, f=0 | YS=1, f=1 | YS=0, f=1 | YS=1, f=0 | YS=1, f=1 | |
Максимальное перерегулирование 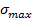
| 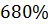
| 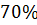
| 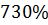
| 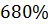
| 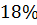
| 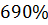
|
Колебательность 
| 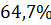
| 
| 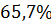
| 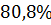
| 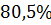
| 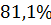
|
| Время регулирования tрегул | 165 с | 170 с | 160 с | 115 с | 95 с | 113 с |
Результаты, полученные с помощью пакета СИМОПТ после оптимизации системы приведены в приложении 2.
Проанализировав таблицу прогона модели до оптимизации и после можно сделать следующие выводы:
1) После проведения оптимизации, показатели качества системы заметно улучшились.
2) В случае YS=1, f=0 (после оптимизации) система стала работоспособна, т.к. удовлетворяет требованиям к показателям качества для работоспособных систем.
3) В случае YS=0, f=1 (после оптимизации) перерегулирование составило 680%, что не удовлетворяет требованиям к показателям качества. Вероятно, это обуславливается исходными параметрами объекта.
4) В случае YS=1, f=1 (после оптимизации) перерегулирование составило 690%, что не удовлетворяет требованиям к показателям качества. Вероятно, это также обуславливается исходными параметрами объекта (инерционного звена первого порядка).
Выбор среды
Для создания проекта был выбран язык программирования JAVA.
Программы на Java транслируются в байт-код, выполняемый виртуальной машиной Java (JVM) — программой, обрабатывающей байтовый код и передающей инструкции оборудованию как интерпретатор, но с тем отличием, что байтовый код, в отличие от текста, обрабатывается значительно быстрее.
Достоинство подобного способа выполнения программ — в полной независимости байт-кода от операционной системы и оборудования, что позволяет выполнять Java-приложения на любом устройстве, для которого существует соответствующая виртуальная машина. Другой важной особенностью технологии Java является гибкая система безопасности благодаря тому, что исполнение программы полностью контролируется виртуальной машиной. Любые операции, которые превышают установленные полномочия программы (например, попытка несанкционированного доступа к данным или соединения с другим компьютером) вызывают немедленное прерывание.
Основные возможности:
- автоматическое управление памятью;
- расширенные возможности обработки исключительных ситуаций;
- богатый набор средств фильтрации ввода/вывода;
- набор стандартных коллекций, таких как массив, список, стек и т. п.;
Так как JAVA не имеет собственной среды разработки(IDE), то для для реализации задачи была выбрана NetBeans IDE 8.0.2.
NetBeans IDE – бесплатная интегрированная среда разработки, с открытым исходным кодом для разработчиков программного обеспечения.
Основные характеристики NetBeans IDE:
1) Рабочая область среды IDE является полностью подстраиваемой под пользователя.
2) IDE имеет в своем составе расширенный многоязыковой редактор для различных языков программирования, в том числе Java.
3) Производится проверка ошибок во время ввода, отображение вариантов для автозавершения кода и фрагментов документации по требуемому языку программирования.
4) Браузер классов позволяет просматривать иерархию и структуру любого класса Java - отображаются интерфейсы, базовые классы, производные классы и члены классов.
Блок схема
Выводы по главе 3
В главе описывается выбор и обоснование среды программирования. На основании приведенных в главе 1 методов моделирования САУ, произведена программная реализация системы. В программной интерпретации был использован математический метод решения дифференциальных уравнений (метод Эйлера - Коши) при моделировании объекта управления.
По окончании работы программы c помощью графического пакета Microsoft Excel были построены графики переходного процесса системы, которые представляются для трех случаев: YS=0 & f=1, YS=1 & f=0, YS=1 & f=1. Составим сводную таблицу показателей качества системы после прогона в системе СИМОПТ (без оптимизации) и в разработанной программе (таблица 13).
Таблица 13.
Сравнение показателей программной реализации и реализации в СИМОПТ
| Критерии качества АСР | СИМОПТ | Программная реализация | ||||
| YS=0, f=1 | YS=1, f=0 | YS=1, f=1 | YS=0, f=1 | YS=1, f=0 | YS=1, f=1 | |
Максимальное перерегулирование 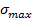
| 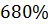
| 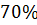
| 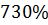
| 
| 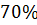
| 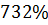
|
Колебательность 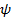
| 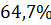
| 
| 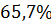
| 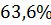
| 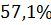
| 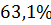
|
| Время регулирования tрегул | 165 с | 170 с | 160 с | 178 с | 170 с | 167 с |
Анализируя таблицу показателей качества полученных после прогона в программе SimOpt и разработанной программе, можно сделать вывод, что присутствует незначительное отклонение показателей качества, полученных с помощью программной реализации, от показателей качества, полученных после прогона модели в программе SimOpt. Таким образом, можно сделать вывод, что программная реализация составлена верно. В ходе программного моделирования оптимизация не производится.
Заключение
В курсовой работе приведены основные понятия и определения теории автоматического управления, основные понятия и определения моделирования динамических систем, в том числе численные методы решения обыкновенных дифференциальных уравнений. Представлено описание системы имитационного моделирования СИМОПТ, ее архитектуры и рабочего пространства.
В ходе выполнения работы были выполнены следующие задачи:
1. В данной курсовой работе была выполнена программная реализация на языке JAVA в среде NetBeans IDE 8.0.2. имитационной модели системы управления, состоящей из ПИ-регулятора и инерционного объекта 1-го порядка с запаздыванием.
2. Моделирование работы системы управления выполнено для трех случаев: YS=0 & f=1, YS=1 & f=0 и YS=1 & f=1. Данные, полученные в результате моделирования, использованы для построения графиков переходных процессов и фазовых портретов в MS Excel. Определены динамические показатели качества САР.
3. Изучены принципы работы с системой моделирования СИМОПТ, и с ее помощью выполнен прогон имитационной модели для трех выше указанных случаев. Также были определены характеристики переходных процессов, полученных при помощи СИМОПТ.
4. Выполнена оптимизация параметров ПИ-регулятора для всех трех случаев средствами СИМОПТ. Сравнение показателей качества переходных процессов, построенных при заданных настройках регулятора и оптимальных, показывает их значительное улучшение при использовании оптимальных настроек.
Список литературы
1. Автоматизированное проектирование систем управления. Под ред. М. Джамшиде, Ч. Дж. Херчета. - М.: Машиностроение, 1989. - 340 с.
2. Кельтон В., Лоу А. Имитационное моделирование. – СПб.: Питер; Киев: Издательская группа ВНV, 2004. – 847 с.
3. Клиначёв Н. В. Теория систем автоматического регулирования и управления: Учебно-методический комплекс. - Offline версия 3.6. - Челябинск, 2005. - 652 файла, ил.
4. Максимей И. В. Имитационное моделирование на ЭВМ. -М.: Радио и связь, 1988. – 231 с.
5. Монахов, В. В. Язык программирования Java и среда NetBeans. – 3-е изд., перераб. и доп. – СПб.: БХВ-Петербург, 2011. – 704 с.
6. Советов Б.Я. Моделирование систем: Учеб. для вузов. – М: Высш. Шк., 2005.- 343 с.
7. Эккель, Б. Философия Java. Библиотека программиста. – 4-е изд., перераб. и доп. – СПб.: Питер, 2009. – 638 с.
8. Конспект лекций по дисциплине "Основы теории управления" для студентов, обучающихся по специальности 220100 – Вычислительные машины, комплексы, системы и сети [Электронный ресурс]: в составе учебно-методического комплекса / разраб. С.И. Суркова; Тверской гос. техн. ун-т, Каф. ЭВМ - Тверь: ТГТУ, 2011.
9. Методические указания к лабораторной работе [Электронный ресурс]: по дисциплине "Проектирование ВС" для студентов, обучающихся по специальности 220100 - Вычислительные машины, комплексы, системы и сети;в составе учебно-методического комплекса. № 4 / разраб. В.А. Григорьев; Тверской гос. техн. ун-т, Каф. ЭВМ - Тверь: ТвГТУ, 2009.
10. Суркова, С.И., Хабаров, А.Р., Лебедев, В.В. Анализ и синтез САР [Электронный ресурс]: в составе учебно-методического комплекса; метод. указ. к лаб. работам по курсу "Теория автоматического управления" / Тверской гос. техн. ун-т, Каф. ЭВМ - Тверь: ТГТУ, 2004.
Приложение 1.
Результаты, полученные с помощью пакета СИМОПТ до оптимизации системы.
1). Графический результат для YS =0, f =1
Переходная характеристика
Фазовый портрет
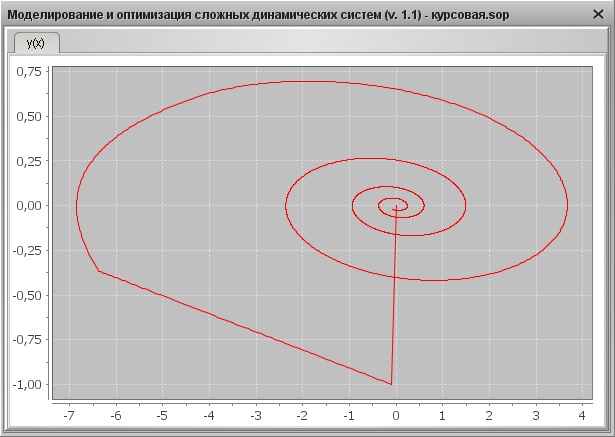
2). Графический результат для YS =1, f =0
Переходная характеристика
Фазовый портрет
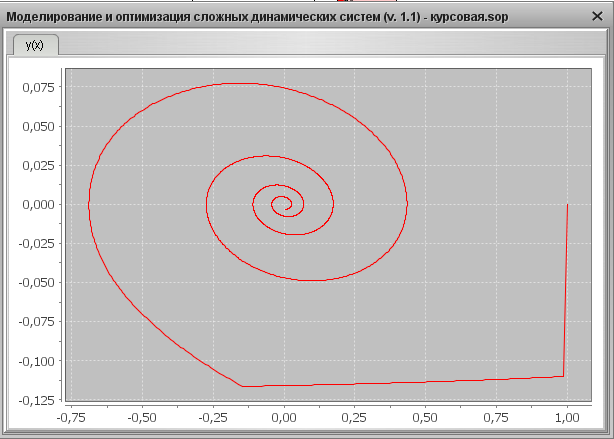
3). Графический результат для YS =1, f =1
Переходная характеристика
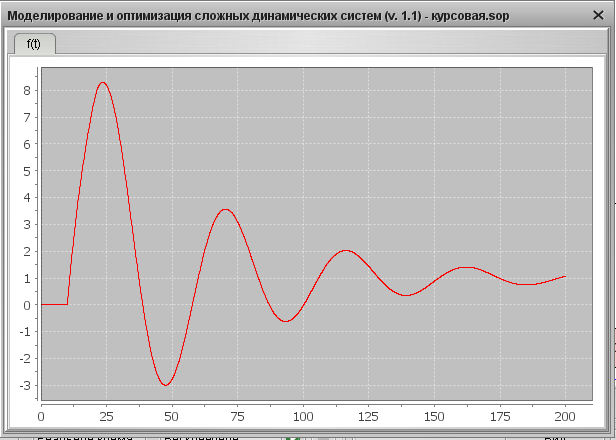
Фазовый портрет
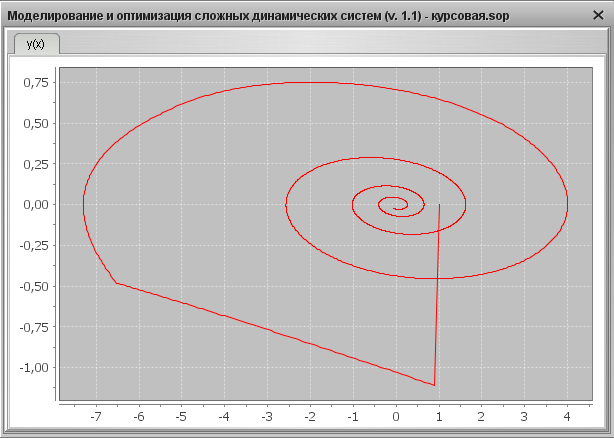
Приложение 2.
Результаты, полученные с помощью пакета SimOpt после оптимизации системы.
1) Графический результат для YS =0, f =1
Переходная характеристика

Фазовый портрет
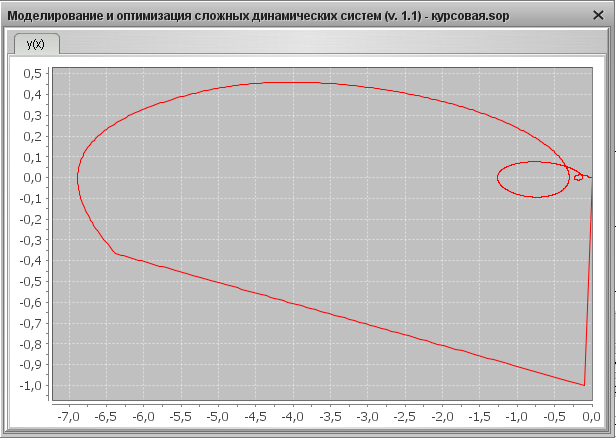
2) Графический результат для YS =1, f =0
Переходная характеристика
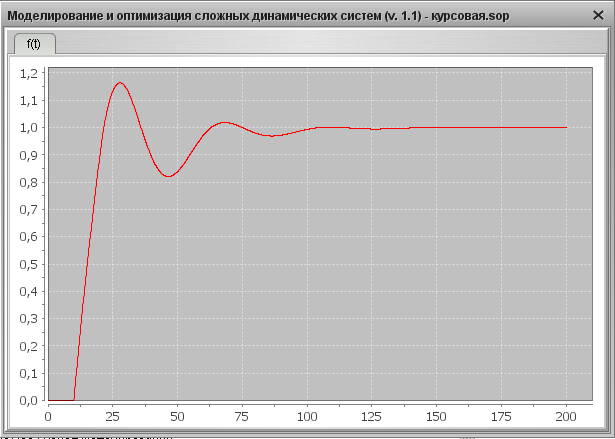
Фазовый портрет
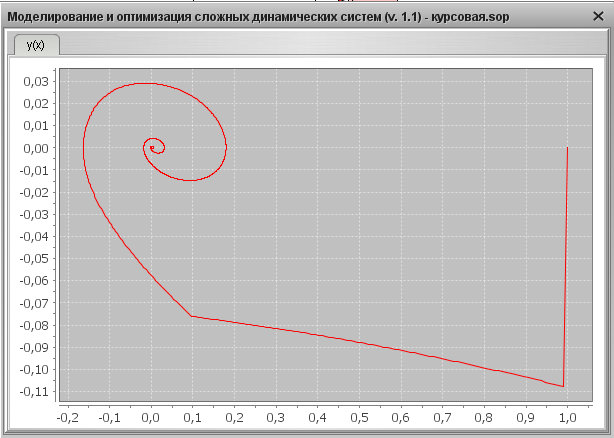
3) Графический результат для YS =1, f =1
Переходная характеристика
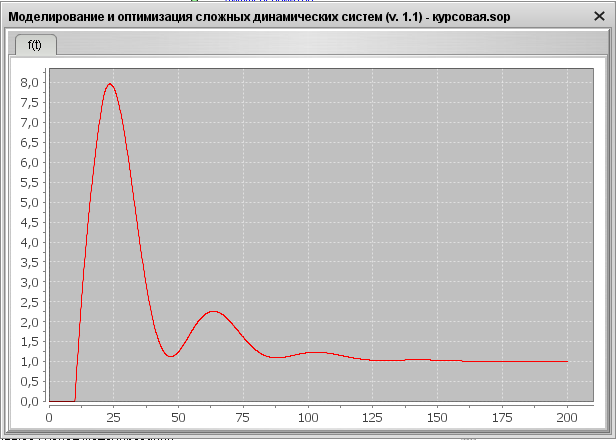
Фазовый портрет
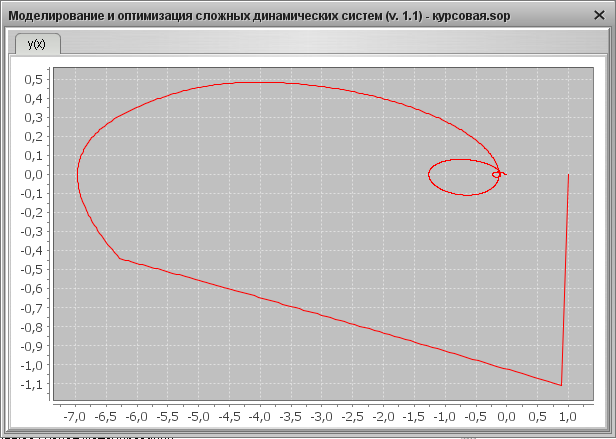
Приложение 3.
Программная реализация. Листинг с комментариями
package simulationmodel;
import java.io.File;
import java.io.IOException;
import jxl.Workbook;
import jxl.write.Number;
import jxl.write.NumberFormat;
import jxl.write.WritableCellFormat;
import jxl.write.WritableFont;
import jxl.write.WritableSheet;
import jxl.write.WritableWorkbook;
import jxl.write.WriteException;
import jxl.write.biff.RowsExceededException;
public class SystemModelling {
private static WritableWorkbook workbook;
private static WritableSheet sheet;
private static double K1, K2, T, TAY, K; // Стартовые условия
private static double YS, F; // Задание и возмущение
private static double T0, TK, HT, X1, XP, X2, U, XT, YX, Y, IT, C1, C2, Y1; // Доп.параметры системы
private static int N1;
private static double[] YR; // Массив запаздывания
public static void main(String[] args) throws RowsExceededException,
WriteException, IOException {
createWorkbookSheet();
initializeVariable();
initializeAdditionalValues();
calculationValues();
}
private static void initializeVariable() {
System.out.print("Инициализация входных параметров системы...");
K1 = 0.11;
K2 = 0.012;
T = 10;
K = 10;
TAY = 10;
YS = 1;
F = 0;
System.out.println(" Входные параметры заданы!");
}
private static void initializeAdditionalValues() {
System.out.print("Инициализация дополнительных параметров системы...");
T0 = 0; // Начало моделирования
TK = 200; // Конец моделирования
HT = 0.1; // Шаг моделирования
X1 = 0; // Ошибка
XP = 0; // Пред. значение ошибки по заданию
X2 = 0; // Производная ошибки по заданию
U = 0; // Выход регулятора
XT = 0; // Выход регулятора с возмущением
YX = 0; Y = 0; // Выход системы
IT = 0; // Интеграл
C1 = 0; C2 = 0; Y1 = 0; //вспомогательные коэффициенты и производная метода Эйлера
N1 = 0;
System.out.println(" Дополнительные параметры заданы!");
}
private static void calculationValues() throws WriteException, IOException {
//обнуление предыдущего значения сигнала
XP = 0;
Y = 0;
YX = 0;
XT = 0;
//обнуление интеграла
IT = 0;
//определение размера массива запаздывания
N1 = (int) (TAY / HT);
YR = new double[N1];
for (int i = 0; i < N1; i++)
// Обнуление массива
YR[i] = 0;
int i = 0;
int p = 0;
int pos = 0;
C1 = K / T;
C2 = -1 / T;
do { // Цикл по процессу моделирования
X1 = YS - Y; // Значение ошибки
X2 = (X1 - XP) / HT; // Производная ошибки
XP = X1;
IT = IT + ((X1 + XP) / 2) * HT; // Интеграл
U = K1 * X1 + K2 * IT; // Управляющее воздействие
XT = F + U; // Выход регулятора с возмущением
Y1 = C1 * XT + C2 * YX; //метод Эйлера
YX = YX + Y1 * HT; // Выход объекта
Y = YR[i]; //запоминаем очередное запаздывание
YR[i] = YX; // Вычисление запаздывания
i++;
if (i >= N1)
i = 0;
if (p >= 0) {
addRowValue(pos, T0, Y, X1, X2);
pos++;
}
T0 = T0 + HT;//прибавление на шаг
p++;
} while (T0 < TK);
addRowValue(pos, T0, Y, X1, 0);
saveFile();
}
private static void createWorkbookSheet() {
System.out.print("Создание нового файла...");
File excelFile = new File("SimulationModel.xls");
System.out.println(" Файл создан!");
try {
workbook = Workbook.createWorkbook(excelFile);
System.out.print("Создание рабочего листа...");
sheet = workbook.createSheet("export", 0);
} catch (IOException e) {
e.printStackTrace();
}
System.out.println(" Рабочий лист создан!");
}
private static void addRowValue(int pos, double T0, double Y, double X1,
double X2) throws WriteException {
WritableFont numberFont = new WritableFont(WritableFont.ARIAL);
WritableCellFormat numberFormat = new WritableCellFormat(numberFont,
new NumberFormat("#0.0000000"));
sheet.addCell(new Number(0, pos, T0, numberFormat));
sheet.addCell(new Number(1, pos, Y, numberFormat));
sheet.addCell(new Number(2, pos, X1, numberFormat));
sheet.addCell(new Number(3, pos, X2, numberFormat));
}
private static void saveFile() throws IOException, WriteException {
System.out.print("Записываем данные на лист, сохраняем файл...");
workbook.write();
workbook.close();
System.out.println(" Готово!");
}
}
Приложение 4.
1) Графический результат для YS =0, f =1
Переходная характеристика
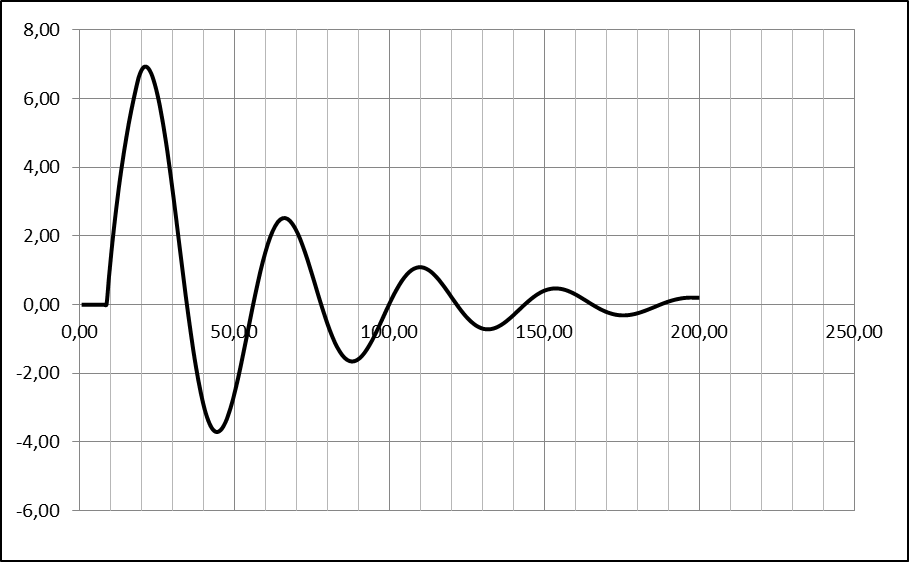
Фазовый портрет
2) Графический результат для YS =1, f =0
Переходная характеристика
Фазовый портрет
3) Графический результат для YS =1, f =1
Переходная характеристика
Фазовый портрет
Введение
Моделирование является важнейшим средством анализа и синтеза сложных систем, к которым с полным основанием следует отнести автоматизированные и автоматические системы управления.
Постоянное ужесточение требований к проектам, чрезвычайно высокая цена ошибочных проектных решений и сложность современных объектов проектирования, особенно систем автоматического управления (САУ), входят в противоречие с традиционными инструментами и технологиями проектирования. Выходом из положения является разработка и внедрение нового инструментария проектировщика – системы автоматизации проектирования.
Умение применять инструменты основывается на понимании того, каким образом строится система моделирования, ее структура и отдельные подсистемы, и на знании математических моделей, методов и алгоритмов, которые положены в основу подсистем системы моделирования.
Существующие и проектируемые системы можно эффективно исследовать с помощью математических моделей (аналитических и имитационных), реализуемых на современных ЭВМ, которые в этом случае выступают в качестве инструмента экспериментатора. Такой эксперимент для инженера есть инструмент непосредственного решения организационно-технических задач.
Математическое моделирование динамики САУ позволяет значительно уменьшить объемы макетных испытаний и осуществить:
· анализ функционирования САУ, их устройств и элементов;
· исследование влияния изменения параметров и возмущающих воздействий на стабильность характеристик САУ;
· выбор структурной схемы САУ по задаваемым критериям;
· оценку устойчивости, динамических и статических ошибок для различных значений параметров выбранной структурной схемы и возмущающих воздействии.
Достаточно трудно указать область человеческой деятельности, где не применялось бы моделирование. В настоящее время большое внимание уделяется задачам оценки характеристик сложных систем на основе имитационных моделей.
Объект исследования данной работы – система автоматического управления, состоящая из ПИ-регулятора и инерционного объекта с запаздыванием.
Предмет исследования – динамические свойства заданной САУ.
Целью данной работы является анализ и оптимизация динамических свойств САУ программным методом и с помощью системы имитационного моделирования СИМОПТ.
Структура работы обусловлена предметом, целью и задачами исследования. Работа состоит из введения, 3 глав, заключения.
Введение раскрывает актуальность, определяет объект, предмет, цель и задачи исследования.
В первой главе рассматриваются основные понятия и определения теории автоматического управления, основные понятия и определения моделирования динамических систем, в том числе численные методы решения обыкновенных дифференциальных уравнений (метод Эйлера, метод Рунге-Кутта 4-го порядка, метод трапеций). Приведено описание системы имитационного моделирования СИМОПТ, ее архитектуры и рабочего пространства.
Во второй главе представлена практическая часть работы, выполненная в системе СИМОПТ. Описан порядок сборки имитационной модели, задания параметров системы, процесса прогона модели. Рассчитаны качественные характеристики автоматической системы управления (АСР) до и после оптимизации модели.
В третьем разделе представлена программная реализация отдельных компонентов системы, блок-схема реализации процесса моделирования, рассчитаны качественные характеристики прогона программной модели.
В заключении подводятся итоги исследования, формируются окончательные выводы.
Работа содержит 4 приложения, где приведен листинг разработанной программы и результаты работы программы.
Задание на курсовую работу
Дана структурная схема объекта управления (Рис.1).

Рис. 1. Структурная схема исходной САУ
САУ состоит из инерционного звена 1 порядка и звена запаздывания. Согласно варианту заданы параметры системы в Таблице 1.
Таблица 1.
Параметры САУ
| № варианта | k | Т | к1 | к2 |
|
| ||||
| 10 | 10 | 0,11 | 0,012 | |
Задачи работы:
1. Выполнить программную реализацию имитационной модели системы управления в заданных режимах работы, состоящей из ПИ-регулятора и инерционного объекта с запаздыванием.
2. В качестве результата вывести фазовый портрет и графики переходного процесса при единичном воздействии (с использованием графической подсистемы Excel).
3. Реализовать прогон модели на системе имитационного моделирования СИМОПТ для двух указанных случаев.
4. Выполнить оптимизацию параметров модели в СИМОПТ. Представить результаты оптимизации.
5. Представить в качестве результатов оптимизации графики переходных процессов и фазовые характеристики при нулевом и единичном воздействии.
6. Оценить параметры системы до и после оптимизации.
Имитационное моделирование проводить для случаев:
1) f=0, YS=1;
2) f=1, YS=0;
Примечание:
1) постоянные времени объекта, транспортное запаздывание и характеристики регулятора k1, k2 выбираются из таблицы 1 (согласно варианту по списку группы) или рассчитываются по методике ;
2) для реализации программной модели инерционного звена используется метод Эйлера.
I. Теоретическая часть
Теория автоматического управления
1.1.1. Основные понятия и определения
Задача автоматизации состоит в осуществлении автоматического управления технологическими или производственными процессами. Управление, имеющее своей задачей изменение по заданному закону или поддержание в установленных пределах физической величины, называется регулированием.
Теория автоматического управления (регулирования) изучает общие принципы построения систем автоматического управления, правила и методы исследования процессов в этих системах.
При решении любой задачи управления необходимо рассматривать объект управления.
Объект управления – техническое устройство, технологический процесс или более простая система управления. Состояние объекта управление определяется рядом величин, характеризующих как воздействия на объект внешней среды и управляющих устройств, так и протекание (Рис. 2).
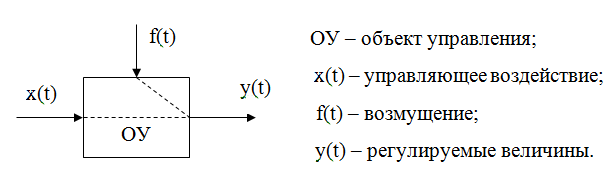
Рис. 2. Блок-схема объекта управления
При изображение системы управления (регулирования) применяются два принципа: функциональный и структурный.
Функциональная схема – блок-схема системы, заданная функциональным назначением элементов.
Структурная схема – блок-схема системы, заданная математическими характеристиками элементов.
После выбора элементов функциональной схемы требуется произвести ее расчет с целью обеспечения заданных показателей качества работы САР. Этим занимается линейная теория автоматического регулирования (ЛТАР). С точки зрения ЛТАР безразлично, из каких элементов составлена САР, важно лишь математическое описание этих элементов.
Для получения математического описания системы обычно составляют описание её отдельных элементов. В частности, для получения уравнения системы, составляют уравнения отдельных элементов. Совокупность этих уравнений и даёт уравнение системы.
Уравнения, а также структурные схемы автоматической системы называют ее математической моделью.
Математические модели описывают элементы и системы автоматического регулирования в двух режимах: установившемся – статике и переходном – динамике. В рамках данной работы целесообразно рассмотреть элементы САР в динамическом режиме.
Дата: 2019-07-30, просмотров: 516.
 =1 сек
=1 сек