1.2.1. Основные понятия и определения

Под моделированием объекта понимается воспроизведение и исследование другого объекта подобного оригиналу в форме, удобной для исследования, и перенос полученных результатов на моделируемый объект. При этом объекты считаются подобными, если характеристики процессов, протекающих в них отличаются от соответствующих характеристик другого объекта вполне определенными и постоянными коэффициентами в течение одного процесса.

Существуют различные методы моделирования:

· геометрическое моделирование

· физическое моделирование

· моделирование методом прямых аналогий

· математическое моделирование

· полунатурное моделирование

Каждый из методов имеет свои плюсы и минусы. Применение конкретного метода обусловлено исследуемой системой и условиями ее работы.

В данной курсовой работе рассматривается только математическое моделирование. При математическом моделировании в качестве объекта моделирования выступают исходные уравнения, представляющие математическую модель объекта, а в качестве модели системы выступают те процессы, которые воспроизводятся на ЭВМ и решают по заданным уравнениям поведение отдельных компонент и их взаимосвязь в системе.

Моделирование на вычислительных машинах часто называют аналоговым и цифровым моделированием. Имитационное моделирование рассматривают также как управляемый эксперимент, проводимый не на реальном объекте, а на модели подобной оригиналу. В этом случае оценивается поведение отдельных компонент, входящих в систему в условиях направленного эксперимента: заданных входных координатах возмущений, параметрических и внешних случайных воздействий.

Характеристики промышленных объектов сведены к типовым характеристикам, поэтому многочисленные законы функционирования регуляторов, работающих с промышленными объектами тоже можно свести к типовым законам, а именно:

· Пропорциональный закон;

· Интегральный закон;

· Пропорционально – интегральный закон;

· Пропорционально – дифференциальный закон;

· Пропорционально – интегрально – дифференциальный закон.

1) Пропорциональный регулятор. Описывается в динамике следующим уравнением (1.2.1).

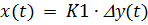 (1.2.1)

Любой регулятор по отношению к объекту, являющейся неизменной частью системы, можно считать последовательным корректирующим звеном, поэтому для определения влияния регулятора на систему найдем его передаточную функцию и определим, к каким типовым динамическим звеньям его нужно отнести (2.2).

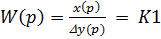(1.2.2)

Пропорциональный регулятор относится к безинерционным звеньям и обеспечивает хорошие динамические свойства системы.

2) Интегральный регулятор. Описывается в динамике следующими уравнениями (1.2.3 и 1.2.4).

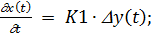 (1.2.3)

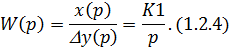
Интегральный регулятор относится к интегрирующим звеньям и обеспечивает хорошие статические свойства системы, но ухудшает при этом динамику систему.

3) Пропорционально – интегральный регулятор. Описывается в динамике следующими уравнениями (1.2.5, 1.2.6).

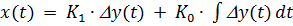; (1.2.5)

Пропорционально – интегральный регулятор можно представить как последовательное соединение безинерционного, интегрирующего и пропорционально – дифференцирующего звеньев. Улучшает и статику и динамику системы.

4) Пропорционально – дифференциальный регулятор. Описывается в динамике следующими уравнениями (1.2.7 и 1.2.8).

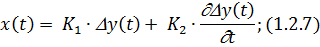
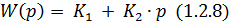
Пропорционально – дифференциальный регулятор можно представить как последовательное соединение безинерционного и пропорционально – дифференцирующего звеньев. Улучшает динамику системы, внося при этом статическую ошибку в систему.

5) Пропорционально – интегрально – дифференциальный регулятор

Описывается в динамике следующими уравнениями (1.2.9 и 1.2.10).

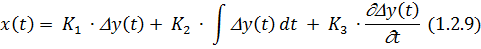
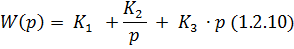
Пропорционально – интегрально – дифференциальный регулятор можно представить как последовательное соединение безинерционного звена, интегрирующего звена и пропорционально – дифференцирующего звена второго порядка. Улучшает как статику, так и динамику системы.