Основные динамические звенья непрерывных динамических систем реализуют определенное дифференциальное уравнение. Рассмотрим наиболее простые методы численного решения дифференциальных уравнений (методы интегрирования).

Будем считать, что исходное ДУ звена представлено в форме Коши:

. 

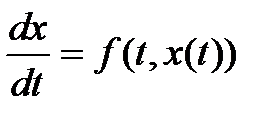    Начальное значение функции .

Метод Эйлера

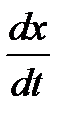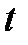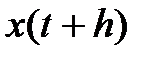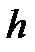Метод Эйлера является простейшим методом интегрирования. Его суть заключается в том, что по известной производной  в момент времени  рассчитывается значение функции , где  – шаг интегрирования (1.2.11).

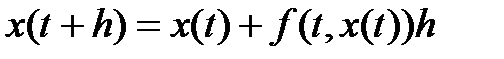.  (1.2.11)

    Геометрической интерпретацией метода Эйлера является построение ломаной прямой искомой функции (рис. 8).

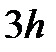
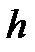
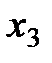
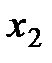
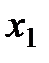
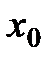
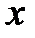
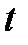
Рис. 8. Геометрическая интерпретация метода Эйлера

Метод Эйлера – единственный метод, который позволяет заранее (за шаг) рассчитать значение искомой функции, но он обладает самой большой ошибкой 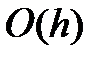 - первый порядок ошибки.

Метод трапеций (метод Хьюна)

Метод трапеций является модификацией метода Эйлера и использует 2 значения входной функции для расчета интеграла. Итерационная формула метода выглядит так (1.2.12).

.   (1.2.12)

Метод трапеций обладает ошибкой второго порядка - .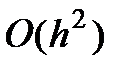

Метод Рунге-Кутта 4-ого порядка

Метод Рунге-Кутта 4-ого порядка обладает в отличие от метода трапеций не 2, а 4 промежуточными вычислениями приращений.

Итерационная формула метода выглядит так (1.2.13)

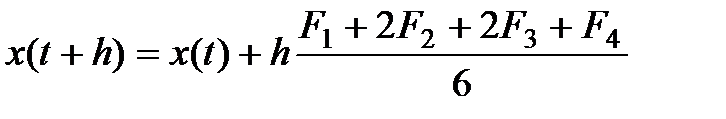,     (1.2.13)

где ;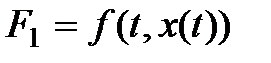

;

.

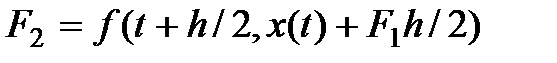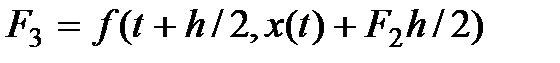
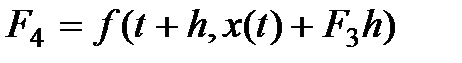Метод Рунге-Кутта 4-ого порядка обладает ошибкой четвертого порядка - .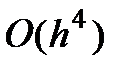

Оптимизация

Оптимизация динамических систем является важной частью моделирующих программ, и ее реализация позволяет значительно увеличить полезность разрабатываемого инструментария.

Оптимизация динамической системы подразумевает нахождение таких ее параметров, которые минимизируют (максимизируют) определенные динамические свойства или характеристики системы. Примером оптимизации динамической системы является нахождение оптимальных настроек регулятора САР, которые позволяют достигнуть наилучшего качества переходного процесса (перерегулирование, время регулирования и т. д.)

Возможны два подхода к решению задачи отыскания минимума функции многих переменных 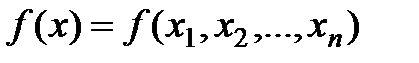 при отсутствии ограничений на диапазон изменения неизвестных.

Первый подход лежит в основе косвенных методов оптимизации и сводит решение задачи оптимизации к решению системы нелинейных уравнений, являющихся следствием условий экстремума функции многих переменных.

Решение систем нелинейных уравнений - задача весьма сложная и трудоемкая. Вследствие этого на практике используют второй подход к минимизации функций, составляющий основу прямых методов. Суть их состоит в построении последовательности векторов 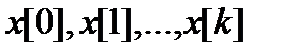, таких, что 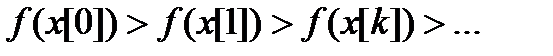. В качестве начальной точки  может быть выбрана произвольная точка, однако стремятся использовать всю имеющуюся информацию о поведении функции , чтобы точка располагалась как можно ближе к точке минимума. Переход (итерация) от точки 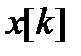 к точке 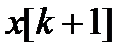, , 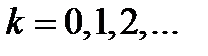состоит из двух этапов:

1) выбор направления движения из точки ;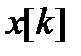

2) определение шага вдоль этого направления.

Методы построения таких последовательностей часто называют методами спуска, так как осуществляется переход от больших значений функций к меньшим значениям.

Математически методы спуска описываются соотношением (1.2.14).

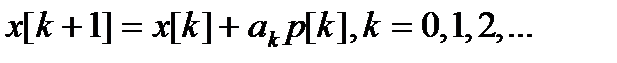                                 (1.2.14)

где 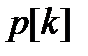 - вектор, определяющий направление спуска;  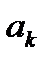- длина шага.

Различные методы спуска отличаются друг от друга способами выбора двух параметров - направления спуска и длины шага вдоль этого направления. На практике применяются только методы, обладающие сходимостью. Они позволяют за конечное число шагов получить точку минимума или подойти к точке, достаточно близкой к точке минимума. Качество сходящихся итерационных методов оценивают по скорости сходимости.

Для организации подсистемы оптимизации в разрабатываемой системе необходимо выбрать методы для реализации, исходя из типа решаемой задачи и качества метода. Специфика оптимизации динамических систем, заданных структурными схемами и неявность задания целевой функции, значение которой может быть рассчитано только после проведения моделирования всей системы в целом обуславливают использования методов нулевого порядка.

Рассмотрим один из методов оптимизации нулевого порядка: метод Хука-Дживса. Выбор данного метода обусловлен: хорошей алгоритмизацией, легкостью реализации; удобством модификации метода для реализации условной оптимизации; наличием тестовых примеров для отладки.

Метод Хука-Дживса

Суть этого метода состоит в следующем. Задаются некоторой начальной точкой . Изменяя компоненты вектора , обследуют окрестность данной точки, в результате чего находят направление, в котором происходит уменьшение минимизируемой функции . В выбранном направлении осуществляют спуск до тех пор, пока значение функции уменьшается. После того как в данном направлении не удается найти точку с меньшим значением функции, уменьшают величину шага спуска. Если последовательные дробления шага не приводят к уменьшению функции, от выбранного направления спуска отказываются и осуществляют новое обследование окрестности и т. д.

Исходными данными для работы метода являются:

1)  – вектор начальных значений;

2) d – начальный шаг поиска;

3) 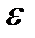 – минимальный шаг поиска.

Ниже представлена блок-схема алгоритма метода Хука-Дживса.

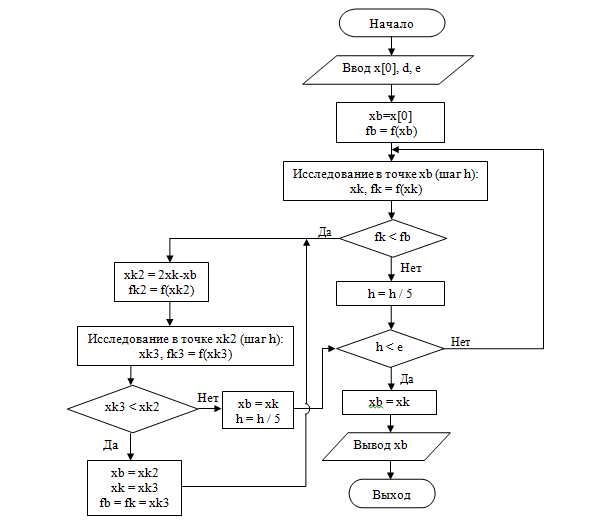
Рис.9 Блок-схема алгоритма метода Хука-Дживса

    Заметим, что величина уменьшение шага в 5 раз выбрана экспериментальным путем, ее изменение может привести к увеличению или уменьшению скорости сходимости метода в зависимости от решаемой задачи.

Выводы по разделу

При математическом моделировании в качестве объекта моделирования выступают исходные уравнения, представляющие математическую модель объекта, а в качестве модели системы выступают процессы, которые воспроизводятся на ЭВМ и решают по заданным уравнениям поведение отдельных компонент и их взаимосвязь в системе.

Пропорционально – интегральный регулятор можно представить как последовательное соединение безинерционного, интегрирующего и пропорционально – дифференцирующего звеньев. Выбор обусловлен тем, что ПИ-регулятор улучшает статику и динамику системы. Пропорциональная составляющая увеличивает быстродействие системы, но приводит к статической ошибке. Интегральная составляющая ПИ-регулятора снижает быстродействие системы, но убирает статическую ошибку.

Метод Эйлера является простейшим методом интегрирования, однако это единственный метод, который позволяет заранее (за шаг) рассчитать значение искомой функции.

Оптимизация динамических систем является важной частью моделирующих программ, и ее реализация позволяет значительно увеличить полезность разрабатываемого инструментария.

Метод оптимизации Хука-Дживса имеет следующие характеристики: хорошей алгоритмизацией, легкостью реализации; удобством модификации метода для реализации условной оптимизации; наличием тестовых примеров для отладки.

СИМОПТ