Построение имитационной модели
Для построения имитационной модели рассмотрим подробнее, что из себя представляет система. По условию данной работы необходимо смоделировать объект регулирования, состоящий из ПИ-регулятора, сумматора на два входа, сравнивающего устройства и объекта управления, представленного инерционным звеном 1-го порядка с запаздыванием. Схема исходного объекта представлена на Рис. 14
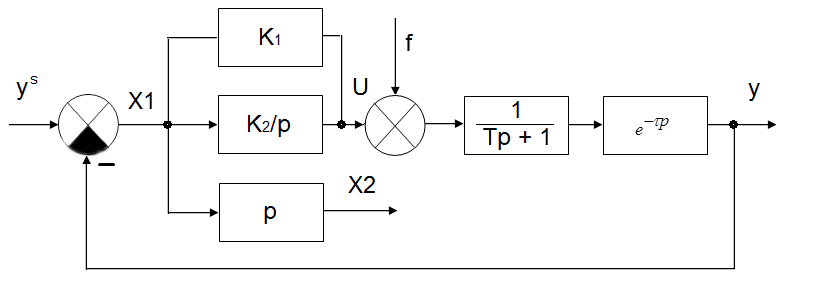
Рис. 14. Структурная схема исходной САУ
Элементы заданной схемы в программе СИМОПТ будут выглядеть следующим образом (таблица 3).
Таблица 3.
Компоненты структурной схемы и их реализация
| Компонент | Реализация | Параметры |
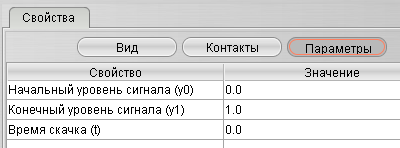
| Задающее воздействие «YS» | 
| 
|
| Возмущение «f» | 
| 
|
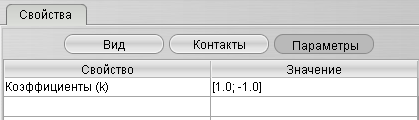
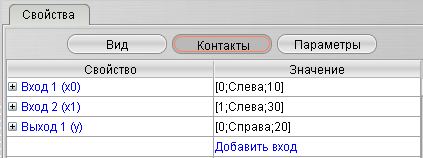
| Сумматор | 
| 
|
| Реализация пропорциональной «k1» и интегральной «k2/p» составляющей | 
| 
|
| Графическое отображение фазового портрета | 
| 
|
| 
| |
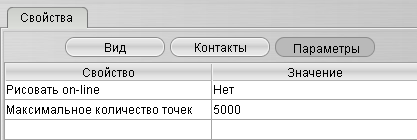
| Графическое отображение переходной характеристики | 
| 
|
| Соединение сигналов «U» и «f» | 
| 
|
| Инерционное звено первого порядка | 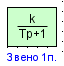
| 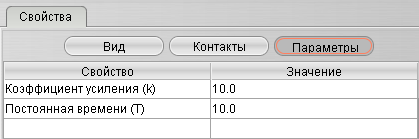
|
| Звено запаздывания | 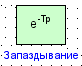
| 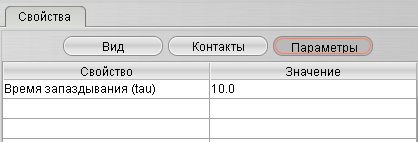
|
| Анализ качества САР | 
| 
|
| 
| |

| 
|
На рис. 15 отражена имитационная модель, которая соответствует указанной в задании структурной схеме. Параметры модели (постоянная времени, транспортное запаздывание и характеристики регулятора Кп, Ки) соответствуют варианту № 10.
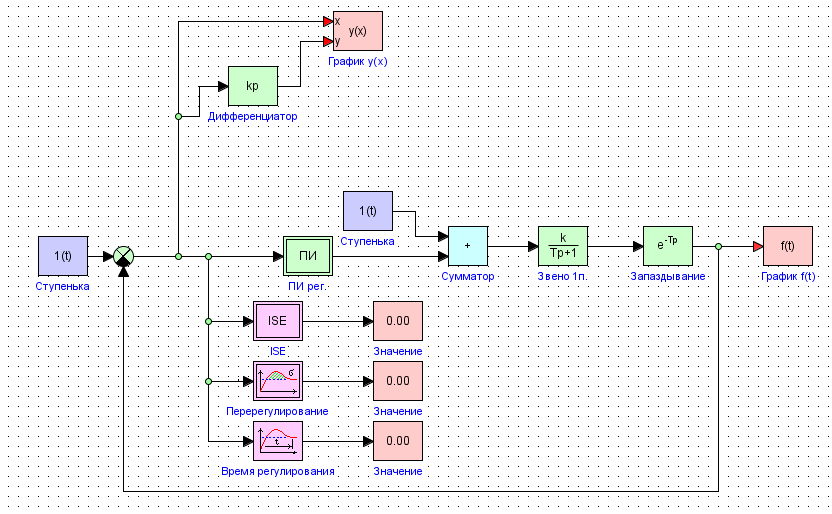
Рис.15. Имитационная модель заданной системы до оптимизации
Оценка параметров системы
Установим шаг моделирования h=0,1 и время моделирования T=200 с.
После окончания моделирования получим значения. Снятие графиков с системы осуществляется двойным щелчком левой кнопкой мыши на компонентах «График f(t)» и «График y(x)».
Нам необходимо рассмотреть несколько вариантов условий, в которых будет работать система. Для начала примем задающее воздействие равное нулю (YS = 0), а на вход объекта управления подадим возмущение в виде «единичной ступеньки» (f = 1). Затем, наоборот, возмущение будет равно 0, а задающее воздействие 1(YS = 1; f = 0). Для третьего случая (YS = 1; f = 1) необходимо будет задать 1 в параметрах ступенек в системе СИМОПТ. Таким образом, согласно поставленной задаче, необходимо провести три прогона системы:
1. YS=0, f=1;
2. YS=1, f=0;
3. YS=1, f=1;
1. Определим показатели качества АСР для случая YS=0, f=1: время регулирования tp, перерегулирование s, колебательность y. Для этого используем переходную характеристику системы, представленную на Рис. 16.
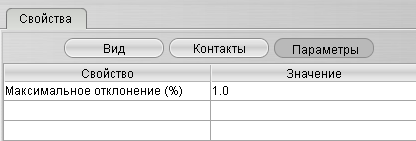
1) Максимальное перерегулирование – максимальное отклонение переходной характеристики от установившегося значения переходной величины, выраженное в относительных единицах.
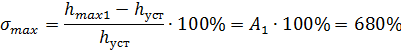
Обычно  .
.
| hуст |
| А4 |
| А3 |
| А1 |
| А2 |
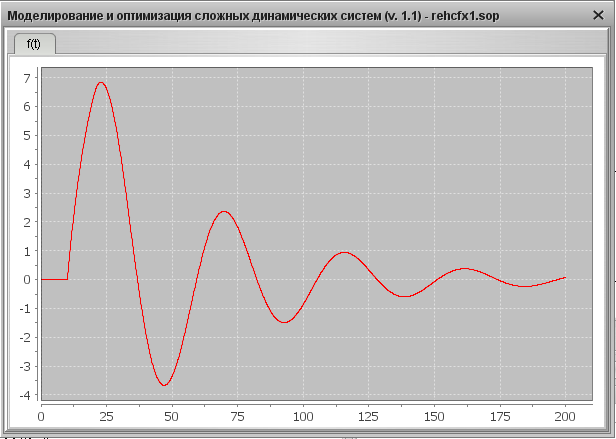
Рис. 16. Переходная характеристика на выходе системы при YS=0, f=1
2) Колебательность процесса
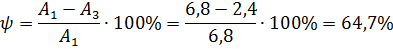
(определяется как отношение разности двух соседних амплитуд, направленных в одну сторону, к большей из них в относительных единицах).
Для работоспособных систем 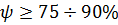
3) Время регулирования – tрегул - минимальное время от начала нанесения возмущения до момента, когда регулируемая величина будет оставаться близкой к установившемуся значению с заданной точностью, т.е. 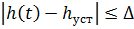 , где Δ – постоянная величина, значение которой нужно оговаривать (обычно Δ=2
, где Δ – постоянная величина, значение которой нужно оговаривать (обычно Δ=2 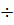 5% hуст). В данном случае время регулирования 165 с.
5% hуст). В данном случае время регулирования 165 с.
Качественные характеристики системы представлены в таблице 4.
Таблица 4.
Показатели качества АСР при YS=0, f=1
| Показатель качества | Значение |
Максимальное перерегулирование 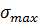
| 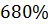
|
Колебательность 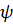
| 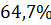
|
| Время регулирования tрегул | 165 с |
На основании проведённых расчётов показателей качества можно сделать вывод, что при YS=0, f=1 система неработоспособна в динамике, т.к. не отвечает требованиям.
2. Определим показатели качества АСР для случая YS=1, f=0: время регулирования tp, перерегулирование s, колебательность y. Для этого используем переходную характеристику системы, представленную на Рис. 17.
| hуст |
| А3 |
| А4 |
| А2 |
| А1 |
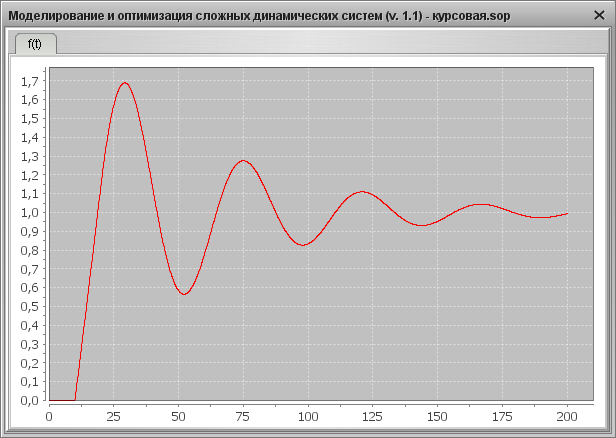
Рис. 17. Переходная характеристика на выходе системы при YS=1, f=0
1) Максимальное перерегулирование:
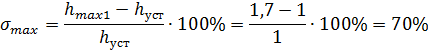
2) Колебательность процесса:
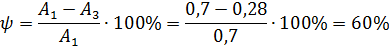
3) Время регулирования в данном случае 170 с.
Качественные характеристики системы представлены в таблице 5.
Таблица 5.
Показатели качества АСР при YS=1, f=0
| Показатель качества | Значение |
Максимальное перерегулирование 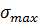
| 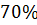
|
Колебательность 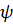
| 
|
| Время регулирования tрегул | 170 с |
На основании проведённых расчётов показателей качества можно сделать вывод, что при YS=1, f=0 система неработоспособна в динамике, т.к. не отвечает требованиям.
3. Определим показатели качества АСР для случая YS=1, f=1: время регулирования tp, перерегулирование s, колебательность y. Для этого используем переходную характеристику системы, представленную на Рис. 18.
| hуст |
| А4 |
| А2 |
| А3 |
| А1 |
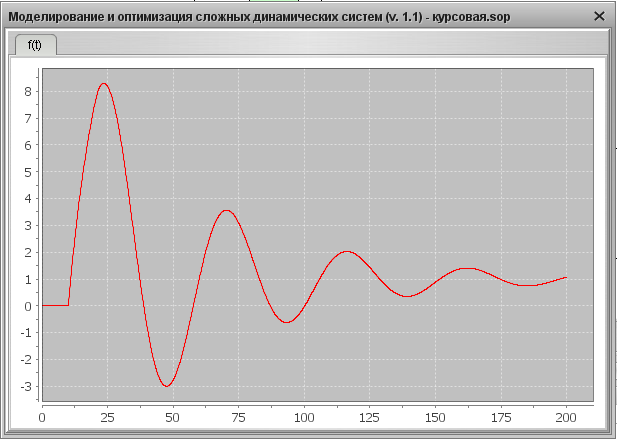
Рис. 18. Переходная характеристика на выходе системы при YS=1, f=1
1) Максимальное перерегулирование:
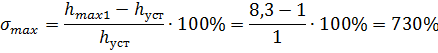
2) Колебательность процесса:
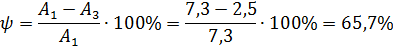
3) Время регулирования в данном случае 160 с.
Качественные характеристики системы представлены в таблице 6.
Таблица 6.
Показатели качества АСР при YS=1, f=1
| Показатель качества | Значение |
Максимальное перерегулирование 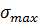
| 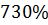
|
Колебательность 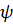
| 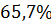
|
| Время регулирования tрегул | 160 с |
На основании проведённых расчётов показателей качества можно сделать вывод, что при YS=1, f=1 система неработоспособна в динамике, т.к. не отвечает требованиям.
Из вышеперечисленных расчетов можно сделать вывод о неработоспособности и неэффективности данной системы во всех трех случаях. Для улучшения показателей требуется оптимизация параметров системы. Результаты, полученные с помощью пакета СИМОПТ до оптимизации системы приведены в Приложении 1.
Дата: 2019-07-30, просмотров: 378.