Основой представления результатов в системе моделирования являются типовые элементы «Временной график f(t)» и «График y(x). Реализация этих объектов основана на использовании свободно распространяемого компонента JFreeChart (рис. 12)
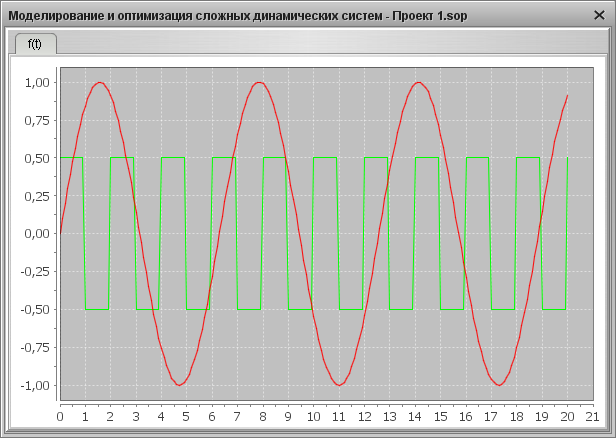
Рис. 12. Компонент JFreeChart
К его достоинствам можно отнести следующее:
· Понятность программных интерфейсов, легкость в интегрировании в приложение;
· Наличие большого количества примеров по реализации;
· Многофункциональность (масштабирование, настройки отображения, сохранение в файл и т.д.)
Использование данного компонента позволило значительно уменьшить время разработки приложения.
Математическое ядро
Основной функцией математического ядра является формирование потока исполнения модели на основе ее структурной схемы. Под потоком исполнения понимается порядок вызова вычислительных процедур блоков модели.
При формировании единого потока выполнения встает ряд трудностей, связанных с:
· Наличием составных элементов (ГЭС);
· Наличием разветвителей сигналов (три графические связи относятся к одному и тому же сигналу);
· Наличием нескольких структурных схем одной модели, сигналы между которыми передаются по специальным блокам;
· Наличие циклов (обратные связи).
Проблема циклов разрешается благодаря так называемым блокам с эффектом памяти. К данным блокам относятся интегратор, звено запаздывания, апериодическое звено 1-ого порядка и т.д. Относительно данных блоков действует закон, на данном шаге выходное значение блока не зависит от его входного значения (действительно только при интегрировании по Эйлеру без использования итерационного решателя). Таким образом данные блоки участвуют в потоке исполнения модели дважды: один раз как генераторы сигнала, а второй раз как приемники сигнала.
Принцип решения первых трех трудностей, связан с требованием, чтобы результирующий поток исполнения не содержал не разветвителей, ни портов ГЭС, ни передающих сигналов блоков. То есть из системы на основе связей изымаются данные блоки и происходит переход от графических связей к сигналам. Каждый сигнал имеет уникальный идентификатор. Для реализации данного перехода используется рекурсивный алгоритм. Результат работы подобного алгоритма показан на рис. 13.
| 4 |
| 2 |
| 5 |
| 5 |
| 3 |
| 1 |
| 2 |
| y(t) |
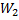
|
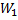
|

| g(t) |
Рис. 13 Результирующая схема с сигналами
Одновременно при работе рекурсивного алгоритма определяется список блоков генераторов сигнала на основе информации о готовности их выходных сигналов (всегда готовы для выдачи). Данные блоки первыми попадают в итоговый поток исполнения.
Затем для каждого генераторного блока по карте схемы находятся блоки приемники сигнала. Если они готовы для расчета, то они также заносятся в поток и сами попадают в конец списка генераторных блоков. Таким образом все блоки заносятся в результирующий поток причем дважды в него попадают только генераторные блоки.
Выводы по разделу
Современные программные средства по моделированию систем различных классов поддерживают принцип визуального моделирования.
Пакеты визуального моделирования позволяют пользователю вводить описание моделируемой системы в естественной для прикладной области и преимущественно графической форме (например, ввод функциональной схемы), а также представлять результаты моделирования в наглядной форме, например, в виде диаграмм или анимационных картинок.
Для дальнейшего эффективного использования программы были приведены диаграмма реализации системы СИМОПТ, описаны архитектура, функциональные возможности, рабочее пространство системы, подсистема представления результатов, математическое ядро и система помощи.
Выводы по главе 1
В первой части главы 1 приведено описание основных понятий и определений теории автоматического управления, способы вычисления динамических показателей качества для системы автоматического регулирования, а также представлены интегральные критерии качества, применяемые для анализа и синтеза систем при имитационном моделировании.
Во второй части приведена характеристика моделирования систем автоматического управления, промышленных регуляторов, объектов управления. Изложены основные методы моделирования, в том числе и метод Эйлера для решения дифференциальных уравнений первого порядка. Рассмотрено понятие оптимизации САУ, в частности метод Хука-Дживса.
В третьей части главы 1 приводится подробное описание пакета СИМОПТ, которое необходимо для реализации модели в данной системе.
На основе вышеперечисленных понятий и методов будет создана программная реализация имитационной модели системы.
Дата: 2019-07-30, просмотров: 373.