В динамике выходная величина звена (системы) изменяется во времени вследствие изменения входной величины. Дифференциальное уравнение аналитически выражает характер изменения во времени выходного параметра при определенном виде входного параметра.
В общем виде дифференциальное уравнение может быть записано следующим образом (1.1.1). Необходимо учесть соотношение параметров системы: m≤ n (условие физической реализуемости).
(1.1.1)
Решение дифференциальных уравнений высоких порядков представляет известные трудности, поэтому сделаны попытки упростить, решение дифференциальных уравнений. Для этого применяют операторный метод, основанный на преобразовании Лапласа.
Смысл преобразования Лапласа заключается в том, что функции действительного переменного х(t) ставится в соответствие функция комплексного переменного x(p), т.е. x(t)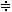 
x(p), где x(t) – оригинал; x(p) – изображение. Операция преобразования записывается так: L{x(t)}=x(p).
Соответствие выражается интегралом Лапласа (1.1.2). Таким образом, с помощью этого интеграла можно от функции x(t) перейти к функции х(p).
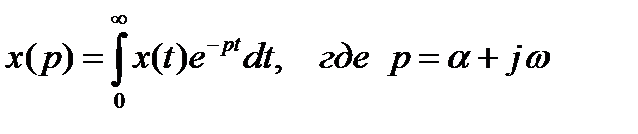(1.1.2)
Для облегчения задачи нахождения оригинала по изображению созданы таблицы преобразования Лапласа, позволяющие не решая интеграла, находить оригинал по изображению и обратно (Таблица 2).
Таблица 2.
Таблица преобразований Лапласа
| Оригинал f(t) | Изображение f(p) |
| 
|
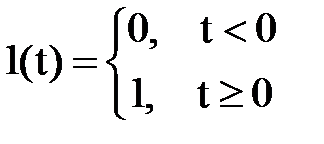
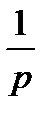
| t | 
|
| kt |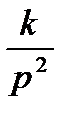 
|
| e-αt |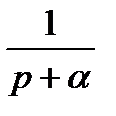 
|
| Sinαt |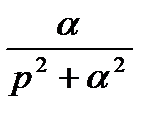 
|
Отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях называется передаточной функцией системы (1.1.3).
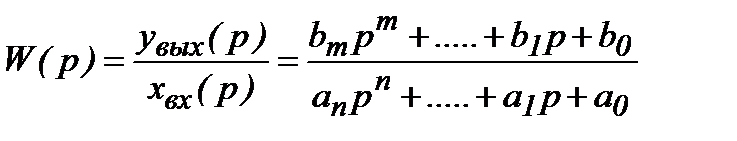(1.1.4)
Статистический коэффициент передачи тоже есть отношение выхода ко входу, но в установившемся режиме (1.1.5.).
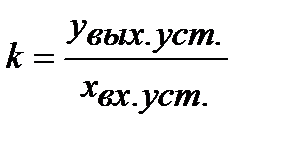, (1.1.5.)
Временные характеристики звена (системы) представляют собой изменение выходной величины во времени при передаче на ее вход типового апериодического воздействия. В качестве последнего используют единичное ступенчатое воздействие или единичный импульс.
При единичном ступенчатом воздействии (Рис. 3) входная величина мгновенно возрастает от 0 до 1 и далее остается неизменной (1.1.6.).
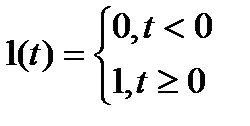(1.1.6.)
| xвх(t) |
| t |
| 1 |
| 0 |
| + |
Рис. 3. Единичное ступенчатое воздействие
Реакция звена на единичную ступенчатую функцию называется переходной характеристикой звена (1.1.7).
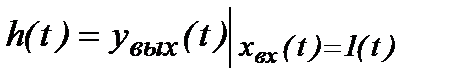(1.1.7)
Реакция звена на единичный импульс [δ(t) – дельта - функция] называется импульсной переходной характеристикой (весовой функцией).
Дельта – функцию [δ(t)] (Рис. 4) определяют как импульс, длительность которого равна 0, амплитуда -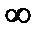 
, а площадь 1, т. е. δ(t) можно определить как производную от 1(t) (1.1.8).
| δ(t) |
| t |
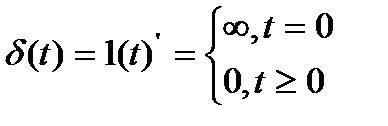(1.1.8)
Рис. 4. Дельта-функция
Частотные характеристики определяют поведение звена (системы) при подаче на его вход гармонического (синусоидального) сигнала.
Пусть xвх(t)=Aвхsin ωt, где Авх=const, ω – круговая частота входного сигнала. На выходе звена (системы) тоже появится гармонический (синусоидальный) сигнал, амплитуда и фаза которого будут другими, зависящими от частоты входного сигнала (1.1.9).
yвых(t)=Aвых(ω)sin[ωt+φвых(ω)] (1.1.9)
Зависимость отношения выходного сигнала к входному от частоты входного сигнала называется комплексной передаточной функцией звена (системы).
Синусоидальный входной сигнал (Рис. 5) можно изобразить вектором ОА на комплексной плоскости, вращающимся вокруг начала координат (1.1.10).
| j |
| Re |
| j |
| A |
| Aвх |
| Jm |
| + |
| 0 |
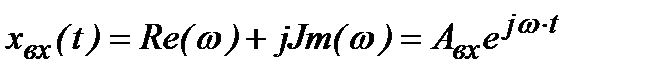(1.1.10)
Рис. 5. Вектор синусоидального входного сигнала
Комплексная передаточная функция 
[K(jω)] может быть записана как (1.1.11).
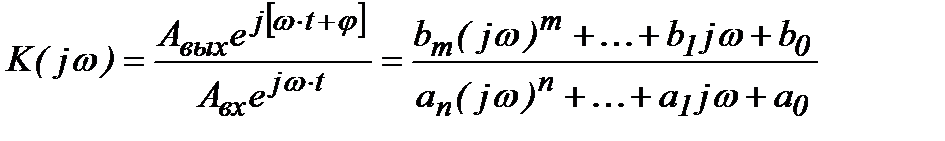(1.1.11)
Сравнив это выражение с выражением передаточной функции будем определять комплексную передаточную функцию звена (системы) из передаточной функции, заменив в ней оператор «р» на оператор «jw» (1.1.12).
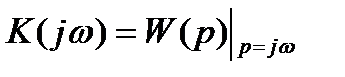(1.1.12)
Из выражения K(jw) видим, что каждой частоте w соответствует вектор K(jw), который при изменении частоты от 0 до ¥ описывает в комплексной плоскости кривую (годограф), называемую амплитудно-фазо-частотной характеристикой звена (системы) (АФЧХ).
АФЧХ показывает одновременно, как изменяется амплитуда и фаза выходного сигнала при изменении частоты входного сигнала.
Типовые звенья САР
Звено системы регулирования – элемент, обладающий определенными свойствами в динамическом отношении. Звенья систем регулирования могут иметь разную физическую основу (электрические, пневматические, механические и др. звенья), но относится к одной группе. Соотношение входных и выходных сигналов в звеньях одной группы описываются одинаковыми передаточными функциями.
Простейшие типовые звенья:
1. Усилительное звено (пропорциональное звено) усиливает входной сигнал в К раз. Уравнение звена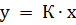 
, передаточная функция 
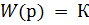. Усилительное звено является безинерционным звеном.
2. Идеальное интегрирующее звено имеет выходную величину пропорциональную интегралу входной величины. При подаче сигнала на вход звена выходной сигнал постоянно возрастает. Уравнение звена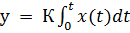 
, передаточная функция 
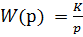. Идеальное интегрирующее звено является астатическим, т.к. не имеет установившегося режима.
3. Реальное интегрирующее звено имеет передаточную функцию 
. Реальное интегрирующее звено является звеном с запаздыванием. Переходная характеристика в отличие от идеального звена является кривой.
4. Идеальные дифференцирующие звенья физически не реализуемы. Реальные дифференцирующие звенья представляют собой дифференцирующие звенья большинства объектов. Переходная характеристика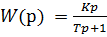 
.
5. Апериодическое (инерционное) звено первого порядка. Переходная характеристика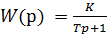 
.
6. Колебательное звено. При подаче на вход ступенчатого воздействия амплитудой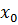 
переходная кривая будет иметь один из двух видов: апериодический (при 
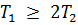) или колебательный (при 
). Переходная характеристика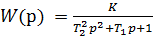 
.
7. Запаздывающее звено. Передаточная функция звена: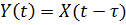 
или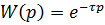 
. Выходная величина 
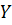повторяет входную величину 
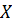с некоторым запаздыванием 
.
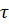Качество САР
В общем случае качество регулирования представляет собой совокупность точности в установившемся режиме и качества переходных процессов.
Оценки качества могут быть прямыми и косвенными. В свою очередь прямые и косвенные могут быть статическими и динамическими. Динамические оценки характеризуют переходной процесс, а статические - установившийся режим.
Качество любой системы регулирования определяется величиной ошибки (1.1.13).
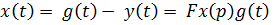(1.1.13)
Однако функцию ошибки x(t) для любого момента времени трудно определить, поскольку она описывается с помощью ДУ высокого порядка, и зависит от большого количества параметров системы. Поэтому оценивают качество САР по некоторым ее свойствам, которые с помощью критериев качества.
Критерии качества регулирования разделяют на 4 группы:
1) Критерии точности – используют величину ошибки в различных типовых режимах.
2) Критерии величины запаса устойчивости – оценивают удаленность САР от границы устойчивости.
3) Критерии быстродействия – оценивают быстроту реагирования САР на появление задающего и возмущающего воздействий.
4) Интегральные критерии – оценивают обобщенные свойства САР: точность, запас устойчивости, быстродействие.
Оценка запаса устойчивости и быстродействия во временной области производится по переходной характеристике при типовом входном или возмущающем воздействии – единичном скачке (Рис. 6).
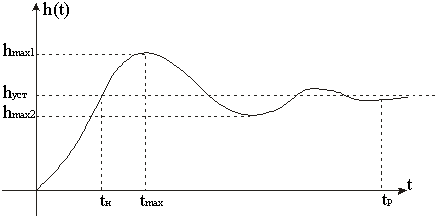
Рис. 6. Переходная характеристика
Если переходная характеристика представляет собой затухающие колебания, то система считается устойчивой. При этом допускается не более 2-3 колебаний.
К основным прямым оценкам относятся следующие: s -регулирование, tp- время регулирования, e - декремент затухания, w - частота колебаний, n - число колебаний, которое имеет переходная характеристика за время регулирования tp, tH - время нарастания переходного процесса, tmax - время достижения первого максимума.
Перерегулирование есть разность между максимальным значением hmax1 переходной характеристики и её установившимся значением, выраженная в процентах (1.1.14).
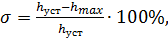(1.1.14)
В большинстве случаев требуется, чтобы перерегулирование не превышало 20 – 30%,
Время регулирования оценивает длительность переходного процесса. За время регулирования принимается тот интервал времени, по истечении которого отклонение переходной характеристики от установившегося значения не превышает некоторой заданной величины q. Значение q выбирают обычно равным 5%.
При заданных значениях s и tp переходная характеристика не должна выходить из определенной области, которая называется областью допустимых отклонений.
В статическом режиме САР оценивается коэффициентом статизма (астатизма) (1.1.15).
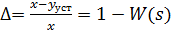, (1.1.15)
где x – задание; yуст - установившееся значение рабочего параметра.
Рассмотренные выше оценки качества относятся к прямым. Вместе с тем существуют косвенные, среди которых наибольшее распространение получили интегральные оценки. Существует две разновидности интегральной оценки: линейная и квадратичная. Численно линейная интегральная оценка равна площади, ограниченной кривой ошибки или разности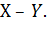 
Значение Y берется в пределах временного интервала от 0 до tp. Линейная интегральная оценка определяется следующим выражением (1.1.16).
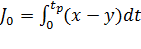(1.1.16)
Эта оценка может быть применена только при монотонных переходных процессах при отсутствии колебаний.
Квадратичная интегральная оценка применяется как при монотонных, так и при колебательных переходных процессах и определяется следующим соотношением (1.1.17).
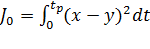(1.1.17)
Недостаток квадратичной интегральной оценки заключается в том, что различные по характеру переходные процессы могут иметь одну и ту же величину оценки. Пример показан на Рис. 7.
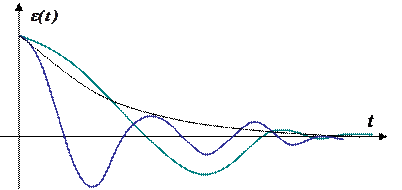
Рис. 7. Типы переходных процессов с одним значением квадратичной интегральной оценки
Выводы по разделу
Совокупность математических описаний элементов системы даёт математическую модель автоматической системы. Математические модели описывают элементы и системы автоматического регулирования в двух режимах: установившемся – статике и переходном – динамике. В рамках данной работы целесообразно рассмотреть элементы САР в динамическом режиме.
Качество регулирования представляет собой совокупность точности в установившемся режиме и качества переходных процессов.
Оценки качества могут быть прямыми (перерегулирование, колебательность, статическая ошибка) и косвенными (линейная и квадратичная интегральная оценка).
Дата: 2019-07-30, просмотров: 294.
