С помощью модели двухтоварного ютиль-анализатора можно показать трехзонную структуру карты кривых безразличия. Если взять два графика взвешенной предельной полезности двух благ «А» и «B» и направить их абсциссы навстречу друг другу, то получим ютиль-анализатор для этих двух благ. По ординате откладываются равные взвешенные предельные полезности, по абсциссе – равные масштабы денежных трат (количественные параметры благ могут отличаться). Оси ординат разводятся на величину предполагаемых денежных трат. Далее абсцисса точки пересечения линий взвешенных предельных полезностей укажет оптимальные объемы потребляемых благ «А» и «B» в случае, если эта точка находится не ниже оси абсцисс (рис. 1).
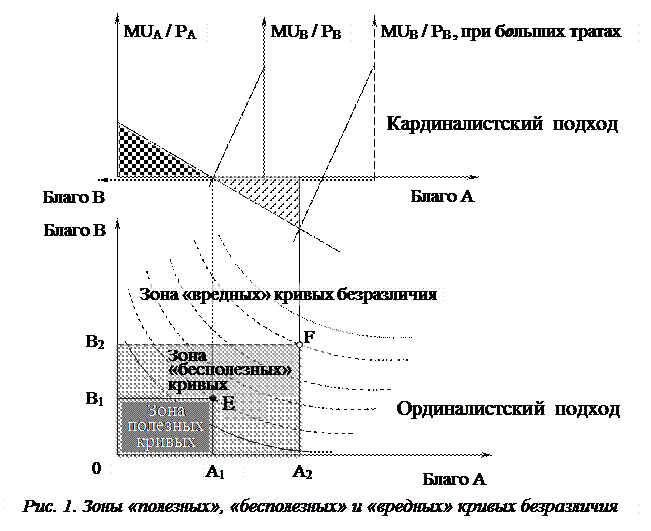
На модели ютиль-анализатора левый треугольник, выделенный шахматными клетками, представляет собой максимальную общую полезность блага «А», которая определяется точкой А1 на ординалистской модели. Дальнейшее увеличение объемов потребления блага «А» приведет к отрицательной области полезности.
Увеличение потребления блага «А» до объемов А2 приведет к тому, что отрицательная общая полезность, обозначенная треугольником, заштрихованным косой линией, сравняется с положительной общей полезностью (треугольник, выделенный шахматными клетками). В этом случае суммарная полезность будет равна нулю. Абсолютно бесполезные траты будут соответствовать точке F (А2 ; В2).
Данная модель показывает, что только в пределах прямоугольника 0А1ЕВ1 кривые безразличия являются полезными кривыми. Любые сочетания благ в этой области не принесут вреда потребителю, а максимальное наилучшее сочетание благ будет соответствовать точке Е (А1 ; В1).
Далее возникают бесполезные траты вплоть до границ прямоугольника 0А2FВ2, за которым находится зона «вредных» кривых безразличия. Любое сочетание благ из той зоны принесет потребителю только вред, так как общая полезность будет иметь всегда отрицательную величину. Ординалистский подход допускает потребительское равновесие в любой точке. Но, как следует из данной модели, равновесие за пределами зоны полезных кривых безразличия носит абсурдный характер, поэтому кривые безразличия всегда необходимо показывать в пределах зоны «полезных» кривых.
2006 г .
Дружеская сделка или рациональное решение
В иррациональной ситуации
Каждый хочет продать подороже, говорит народная мудрость, а купить подешевле. Именно так ведет себя человек экономический (homo ekonomikus). Но бывают такие ситуации, когда цена спроса становится выше цены предложения. Это возникает, когда в экономические отношения «вклиниваются» дружеские связи.
Например, Иванов оказал своему приятелю Петрову хорошую услугу, за которую последний должен заплатить некоторую денежную сумму. (Конечно же, когда в дружеские отношения вмешиваются денежные расчёты, то такие отношения начинают носить рациональный характер, в то время как дружеские отношения основаны исключительно на иррационализме.)
Если бы существовал рынок данных услуг и, соответственно, рыночные цены на такую услугу, то проблема оплаты решалась бы довольно просто: при прочих равных условиях рыночную цену следовало бы поделить пополам и таким образом достичь равных выигрышей в дружеской сделке.
Но если рынок данной услуги отсутствует или нет возможности узнать рыночную цену такой услуги, то как осуществить дружескую сделку при условии обязательной оплаты этой сделки в денежном эквиваленте? Такая ситуация может встречаться довольно часто там, где слабо развит рынок данных услуг или их аналогов.
Петров спрашивает Иванова, сколько стоит его услуга? Но Иванов, пожимая плечами, затрудняется ответить: издержки производства данной услуги минимальны (будем для примера считать, что затрачены только нематериальные активы – время).
– А сколько ты дашь? – спрашивает Иванов Петрова. И тут возникает проблема поиска равновесной цены дружеской сделки.
Иванов готов попросить за услугу 10 рублей (очень удобно получить плату одной купюрой, да так, чтобы не обидеть приятеля высокой ценой), а Петров готов заплатить 50 рублей за услугу (очень удобно отдать одну купюру, по-дружески одаривая за хорошую услугу). Вот здесь-то и возникает эта парадоксальная ситуация, когда не каждый хочет продать подороже, а купить подешевле. (Homo «экономикус» потеснен homo «приятеликусом».)
Как быть? Если Иванов первый скажет, что он готов принять плату 10 рублей, то Петров, чтобы показать свои приятельские отношения, добавит к этой цене, например, ещё 10 рублей и таким образом сделка пойдёт по 20 рублей. А если первым назовёт свою цену Петров, то Иванов из тех же побуждений скинет, к примеру, 10 рублей и тогда сделка пойдёт по 40 рублей (рис. 1).

Рис. 1. Модель парадоксальной ситуации
Как видим, в первом случае выигрывает Петров, а во втором – Иванов. Согласно представленной модели один выигрывает 10 р., а другой контрагент проигрывает 10 р. Причём если сделку проводить таким образом, то проигравший никогда не узнает, что он в этой сделке проиграл и насколько. Тот, кто первый называет свою цену, тот в такой ситуации всегда проигрывает.
Казалось бы, тупиковая ситуация. Решение поиска равновесной цены, когда никто не проигрывает, а оба одинаково выигрывают, заключается в получении информации от двух контрагентов одновременно, так чтобы никто не смог изменить свое решение. Есть простой способ: каждый пишет скрытно на листе бумаги свою цену, потом по этим величинам определяется среднеарифметическая цена (10+50) / 2 = 30 руб. Так оно однажды и было сделано.
2006 г .
Зоны предложения
Анализ кривой предложения позволяет выявить два подхода: подход ценоискателя и ценополучателя. Если при исследовании предложения за независимую переменную принять объемы производства, а за зависимую величину – цены (позиция ценоискателя), то можно выделить две зоны предложения – зону убытков и зону прибыли (рис. 1).
 |

Рис. 1. Структура предложения
Кривая средних издержек АС с точки зрения ценоискателя, это кривая предложения, потому что она ограничивает области прибыли и убытков. Ценоискатель должен находиться всегда в зоне прибыли: кривая средних издержек – это «пол» ценоискателя, а кривая спроса – «потолок».
Если при исследовании предложения за независимую переменную принять цены, а за зависимую величину – объем производства (позиция ценополучателя или объёмоискателя), то ситуация будет выглядеть несколько иначе. Кривая предельных издержек МС не ниже кривой средних издержек АС – это линия, показывающая оптимальные объемы производства в зависимости от цены, то есть линия максимальной прибыли. В классическом представлении это и есть кривая предложения.
Если позиция производителя не определена, то можно заключить, что у него имеются две кривых предложения. Первая кривая предложения – это линия, которая показывает минимальные цены, обеспечивающие производителю нулевую прибыль, в зависимости от объемов производства (кривая средних издержек). Вторая кривая предложения – это линия, которая показывает оптимальные объемы производства, обеспечивающие производителю максимизацию прибыли, в зависимости от цены товара (кривая предельных издержек не ниже кривой средних издержек).
Если производитель – ценополучатель, то он будет ориентироваться на кривую предельных издержек, находящуюся в зоне прибыли, с целью поиска оптимальных объёмов производства. Если производитель – ценоискатель, то он будет ориентироваться на кривую спроса. Если производитель – и ценоискатель, и объёмоискатель, то есть монополист, то он прибегнет к предельному анализу: равенство предельных издержек и предельного дохода позволит найти оптимальные объёмы производства, а они помогут найти «потолок» цен.
Комплексная кривая предложения усреднённого производителя будет состоять из двух частей: первая часть кривой предложения, обозначенная на рисунке буквой А − это часть, минимизирующая издержки (рис. 1), а вторая часть кривой, обозначенная буквой Б – это часть, максимизирующая прибыль.
2004 г .
Карта спроса
Представим себе такую ситуацию: продавцу скоропортящегося товара необходимо через два часа продать весь товар. Возникает закономерный вопрос, по какой цене пустить товар, помня о необходимости максимизации прибыли, чтобы ровно через два часа весь товар был продан, причём не раньше и не позже назначенного срока.
Теоретически ответить на этот вопрос можно, если ввести такое понятие, как карта спроса. На карте спроса изображается множество кривых спроса, соответствующих эффективному времени, то есть времени, в течение которого будет полностью реализован товар при всех допустимых ценах (рис. 1).
Например, если продавец намерен продать свой товар за время t2, то ему необходимо выбрать кривую спроса D(t2) и ввести объемы, подлежащие продаже. Пусть это будет 50 кг, тогда кривая спроса покажет эффективную цену − 20 руб./кг. Если же продавец установит цену 30 руб./кг, то этот же объем товара он продаст за большее время – t3, если цена будет 40 руб./кг, то – за t4. Продавая товар по 20 руб./кг, продавец смог бы продать и 100 кг товара, если бы у него был в распоряжении промежуток времени t4. Если продавцу необходимо продать 25 кг товара за время t2, то ему необходимо установить цену 30 руб./кг, и тогда к назначенному сроку он получит наибольшую прибыль. Таким образом, продавец, располагая реальной картой спроса, мог бы быстро и точно опре
 |
делять эффективную цену на данный товар для конкретных условий.
Рис. 1. Карта спроса
Вместо карты спроса можно использовать эмпирическую формулу, дающую с некоторой долей вероятности эффективную цену при определенных условиях: Р = ((N·k – E·Q)·T·W)1|2, где N·k > E·Q, N − число покупателей в торговом зале, k – поправочный коэффициент платежеспособности и потребности (руб./чел.), E – эластичность спроса по объему продаж (руб./кг), Q – объемы предполагаемых продаж (кг), T – планируемый период времени продажи (ч.)
Т ≠ 0, W – настроечный и регулирующий коэффициент (руб./ч). Например, в торговом зале, где продается единственный скоропортящийся продукт, находятся 100 человек. Коэффициент k = 0,5 руб./чел., Е = 0,5 руб./кг, W = 1 руб./ч. Продавцу необходимо продать 50 кг продукта за 8 часов при прочих равных условиях. Подставляем в формулу известные параметры и вычисляем эффективную цену: Р = ((100 · 0,5 – 0,5 · 50) · 8 · 1)1|2 = 14 руб./кг.
Конечно, в реальности никакие прочие условия не могут быть постоянными, поэтому для большей точности формула эффективной цены должна иметь более сложный вид. В то же время погоня за дополнительными параметрами может усложнить формулу, что потребует много времени для получения выведенных параметров и свести на нет эффективность использования данной формулы. Практичнее всего для определения эффективной цены использовать корректируемые карты спроса. А так как рабочий день у продавцов, как правило, имеет постоянную величину, то большой необходимости в карте спроса не наблюдается. Карта спроса необходима в том случае, когда у продавцов постоянно меняется длительность рабочего времени и (или) постоянно необходимо продавать разные объёмы товаров.
2006 г .
Осторожно, неравновесная цена!
Всемирно известная оригинальная модель Альфреда Маршалла (иначе её называют «Крест Маршалла») позволяет показать важность достижения на рынке равновесной цены. Почему, давайте разберёмся.
Когда цена неравновесная, то на рынке возникают «болезни» – перепроизводство благ или их дефицит. Но самое важное в этом анализе: следует указать на то, что при неравновесных ценах меньшее количество потребителей удовлетворят свои потребности, чем при равновесных ценах (рис. 1).
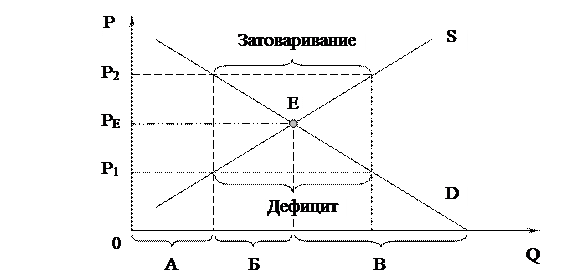
Рис. 1. Модель А. Маршалла
Например, если на оси количества <Q> откладывать количество потребителей, приобретающих одно благо, то фигурной скобкой <A> будут обозначены те потребители, которые удовлетворят свои потребности в данном благе при неравновесных ценах Р1 и Р2. Фигурной скобкой <Б> будут обозначены потребители, которые не смогут удовлетворить свои потребности в данном благе при тех же неравновесных ценах.
При равновесной цене <PE> количество потребителей, которые смогут удовлетворить свои потребности, увеличится и составит сумму: <A> + <Б>. Таким образом, только равновесная цена способна удовлетворить наибольшее количество потребителей в условиях свободного конкурентного рынка. Снижать административным путем равновесные цены по принципу «хотели как лучше …» обязательно приведёт к снижению количества потребителей, которые хотели бы удовлетворить свои потребности в данном благе.
Но, как видно из модели «Крест Маршалла», даже равновесная цена не способна удовлетворить всех членов общества. В условиях свободного рынка определённая часть населения (фигурная скобка <В>) не сможет приобрести эти блага. Поэтому в социальном государстве существует вторичное перераспределение доходов, в результате чего положения кривых спроса и предложения изменяются.
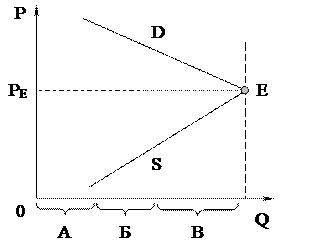 |
Рис. 2. Модель А. Маршала
для социально-рыночного хозяйства
Из рисунка 2 видно, что все категории граждан <A>, <Б>, <В> приобретают данное благо. Перепроизводства или дефицита не наблюдается.
В заключение хотелось бы привести оригинальный вывод студента третьего курса физико-математического факультета Чащина Дмитрия (группа 3А, 2003 г.) при решении задачи «неравновесная цена»: « … Некоторые студенты останутся голодными, что приведёт к росту недовольства в студенческой среде и назреванию мятежа, который перерастёт в бунт, а потом в революцию, что приведёт к развалу экономики государства, затем самого государства, а впоследствии и всего мира. Наступит хаос, и мир вернётся к первобытному строю».
В этом шуточном выводе есть доля истины. В 1917 году в России, «уступая требованиям населения, правительство ещё 25 марта ввело хлебную монополию. Продажа хлеба производилась только государственными органами и по твёрдым ценам»[3]. В результате цены на хлеб стали неравновесными, крестьяне стали придерживать хлеб − величина предложения упала, − и в крупных городах начались перебои с продовольствием, что привело к дальнейшему нарастанию социальной напряженности и октябрьскому перевороту, в дальнейшем названным коммунистами Великой Октябрьской социалистической революцией. Следует добавить, что и Февральская революция в России в 1917 г., и Августовская революция в СССР в 1991 г. были спровоцированы нехваткой продовольствия, к которой привели неравновесные цены.
2008 г .
Дата: 2019-07-30, просмотров: 379.