Кредитно-модульная система – это модель организации учебного процесса, которая основывается на объединении двух составляющих: модульной технологии обучения и кредитов (зачетных единиц) и охватывает содержание, формы контроля качества знаний, навыков и учебной деятельности студента в процессе аудиторной и самостоятельной работы.
Рейтинговая система оценивания – это система определения качества выполненной студентом всех видов аудиторной и самостоятельной работы и уровня приобретенных им знаний и навыков путем оценивания в баллах результатов этой работы во время текущего модульного и полусеместрового итогового контроля, с последующим переведением рейтинговой оценки в баллах в оценки традиционной национальной шкалы и шкалы ECTS.
Рейтинговая оценка состоит из баллов, которые студент получает за определенную учебную деятельность на протяжении усвоения данного модуля – тестирование, выполнение и защита индивидуальных задач (домашних контрольных работ), выполнение аудиторной самостоятельной работы и выступления на практических занятиях и т.п..
Семестровый курс дисциплины "Теория принятия решений" разбит на 4 модуля. В конце каждого модуля проводится модульный контроль в виде аудиторной контрольной работы (АКР) или защиты домашней контрольной работы (ДКР), который оценивается до 25 баллов.
Для модуля №1 максимальный рейтинговый балл – 25 баллов распределяется следующим образом:
- аудиторная контрольная работа – 20 баллов;
- выполнение аудиторной самостоятельной работы и выступления на практических занятиях – 5 баллов.
Для модуля №2 максимальный рейтинговый балл – 25 баллов распределяется следующим образом:
- аудиторная контрольная работа – 20 баллов;
- выполнение аудиторной самостоятельной работы и выступления на практических занятиях – 5 баллов.
Для модуля №3 максимальный рейтинговый балл – 25 баллов распределяется следующим образом:
- домашняя контрольная работа – 20 баллов;
- выполнение аудиторной самостоятельной работы и выступления на практических занятиях – 5 баллов.
Для модуля №4 максимальный рейтинговый балл – 25 баллов распределяется следующим образом:
- аудиторная контрольная работа – 20 баллов;
- выполнение аудиторной самостоятельной работы и выступления на практических занятиях – 5 баллов.
Общая балльная оценка за полусеместр выводится простой суммой полученных студентом баллов за все модули полусеместра. Максимальная полусеместровая оценка составляет 100 баллов. Оценка по национальной шкале выводится в соответствии с таблицей:
| Итоговый рейтинговый балл по дисциплине | Оценка по шкале ECTS | Оценка по национальной шкале |
| 91-100 | A | Отлично |
| 81-90 | B | Хорошо |
| 76-80 | C | |
| 61-75 | D | Удовлетворительно |
| 51-60 | E | |
| 21-50 | FX | Неудовлетворительно |
| 0-20 | F |
Раздел 8. Задания для самостоятельной работы студентов
Домашняя контрольная работа
Согласно рабочей учебной программе дисциплины "Теория принятия решений" в модуле №3 выполняется домашняя контрольная работа.
Цель домашней контрольной работы – детальная и более тщательная проработка лекционного и практического материала, с целью проверки и контроля степени его усвоения, формирование у студентов предусмотренных рабочей программой навыков.
Домашняя контрольная работа выполняется на бумажных носителях.
Домашняя контрольная работа содержит 30 вариантов. Каждый вариант содержит четыре задания:
- задание №1 – решение матричной игры в чистых стратегиях;
- задание №2 – решение матричной игры в смешанных стратегиях симплекс-методом;
- задание №3 – решение матричной игры в смешанных стратегиях графическим методом.
Студент выбирает вариант домашней контрольной работы согласно своему порядковому номеру в журнале списка своей группы. Контрольная работа, не соответствующая своему варианту, не проверяется и к защите не допускается.
Задание №1.
Определить оптимальные чистые стратегии и цену игры:
1 вариант 2 вариант 3 вариант
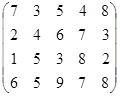
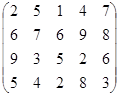
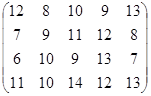
4 вариант 5 вариант 6 вариант
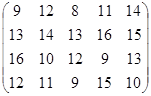
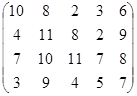
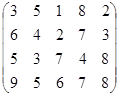
7 вариант 8 вариант 9 вариант
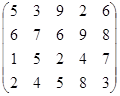
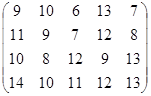
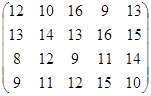
10 вариант 11 вариант 12 вариант
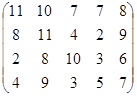
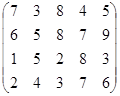
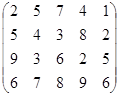
13 вариант 14 вариант 15 вариант
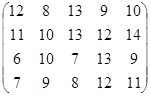
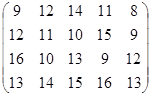
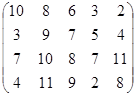
16 вариант 17 вариант 18 вариант
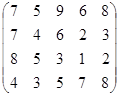
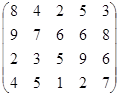
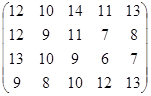
19 вариант 20 вариант 21 вариант
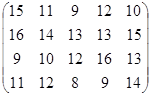
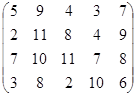
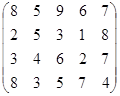
22 вариант 23 вариант 24 вариант
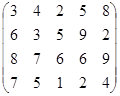
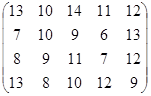
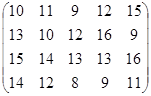
25 вариант 26 вариант 27 вариант
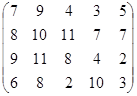
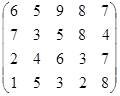
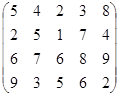
28 вариант 29 вариант 30 вариант
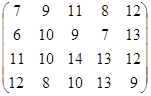
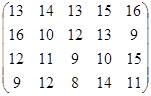
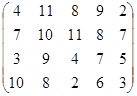
Задание №2.
Определить симплекс-методом оптимальные смешанные стратегии и цену игры:
1 вариант 2 вариант 3 вариант
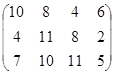
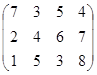
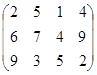
4 вариант 5 вариант 6 вариант
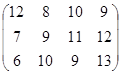
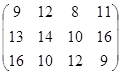
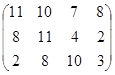
7 вариант 8 вариант 9 вариант
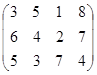
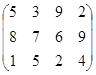
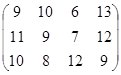
10 вариант 11 вариант 12 вариант
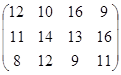
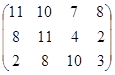
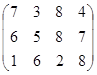
13 вариант 14 вариант 15 вариант
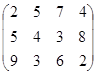
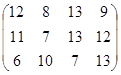
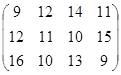
16 вариант 17 вариант 18 вариант
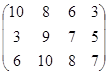
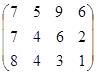
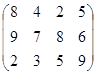
19 вариант 20 вариант 21 вариант
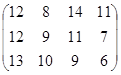
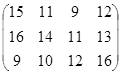
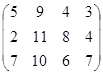
22 вариант 23 вариант 24 вариант
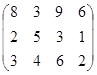
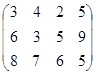
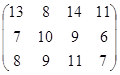
25 вариант 26 вариант 27 вариант
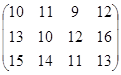
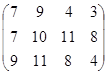
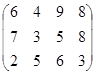
28 вариант 29 вариант 30 вариант
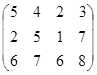
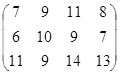
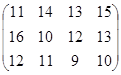
Задание №3.
Определить графическим методом оптимальные смешанные стратегии и цену игры:
1 вариант 2 вариант 3 вариант
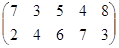
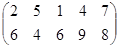
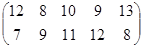
4 вариант 5 вариант 6 вариант
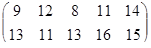
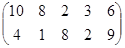
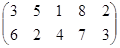
7 вариант 8 вариант 9 вариант
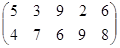
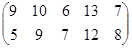
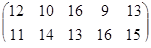
10 вариант 11 вариант 12 вариант
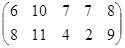
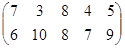
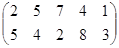
13 вариант 14 вариант 15 вариант
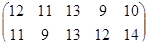
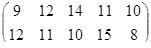
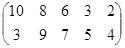
16 вариант 17 вариант 18 вариант
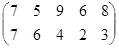
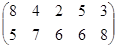
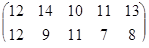
19 вариант 20 вариант 21 вариант
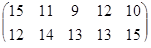
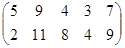
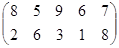
22 вариант 23 вариант 24 вариант
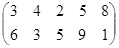
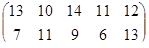
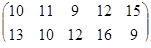
25 вариант 26 вариант 27 вариант
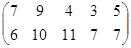
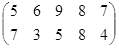
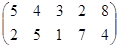
28 вариант 29 вариант 30 вариант
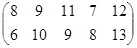
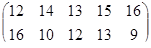
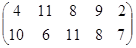
Вопросы к модульным тестированиям
Общие вопросы к всем модулям:
1. Что такое исследование операций?
2. Что такое ЛПР?
3. Что такое математическая модель?
4. Что такое переменные?
5. Что такое альтернатива?
6. Что такое план?
7. Что такое ограничение?
8. Что такое допустимое множество?
9. Что такое допустимый план?
10. Что такое целевая функция?
11. Что такое оптимальный план?
12. Что такое математическое моделирование?
13. Что такое математическое программирование?
14. Что такое линейное программирование?
15. Что такое целочисленное программирование?
16. Что такое динамическое программирование?
17. Что такое нелинейное программирование?
18. Что такое задача принятия решения?
19. Что такое бинарные отношения?
20. Что такое ориентированный граф?
21. Что такое множество Парето?
22. Найти множество Парето.
23. Что такое принятие решения в условиях определенности?
Вопросы к модулю №1:
24. Что такое принятие решения в условиях риска?
25. Какие условия использования критерия Байеса?
26. Решить задачу с помощью критерия Байеса.
27. Какие условия использования критерия Лапласа?
28. Решить задачу с помощью критерия Лапласа.
29. Какие условия использования критерия Гермейера?
30. Решить задачу с помощью критерия Гермейера.
31. Какие условия использования критерия Ходжа-Лемана?
32. Решить задачу с помощью критерия Ходжа-Лемана.
Воп росы к модулю №2:
33. Что такое принятие решения в условиях неопределенности?
34. Какие условия использования принципа максимина?
35. Решить задачу с помощью принципа максимина.
36. Какие условия использования критерия азартного игрока?
37. Решить задачу с помощью критерия азартного игрока.
38. Какие условия использования критерия произведений?
39. Решить задачу с помощью критерия произведений.
40. Какие условия использования критерия Севиджа?
41. Решить задачу с помощью критерия Севиджа.
42. Какие условия использования критерия Гурвица?
43. Решить задачу с помощью критерия Гурвица.
Вопросы к модулю №4:
44. Что такое принятие решения в условиях противодействия?
45. Что такое матричная игра?
46. Что такое платежи матричной игры?
47. Что такое матрица платежей?
48. Что такое матричная игра с нулевой суммой?
49. Что такое матричная игра с ненулевой суммой?
50. Что такое седловая точка?
51. Что такое чистая стратегия?
52. Что такое смешанная стратегия?
53. Найти седловую точку матрицы.
54. Решить матричную игру в чистых стратегиях.
55. Найти множество Парето для задачи двукритериального выбора.
56. Решить задачу многокритериального выбора методом линейной аддитивной свертки.
57. Решить задачу многокритериального выбора методом мультипликативной свертки.
58. Решить задачу многокритериального выбора методом максиминной свертки.
59. Решить задачу про групповую экспертную оценку.
60. Решить задачу экспертной оценки объектов с учетом компетентности экспертов.
8.3 Контрольные вопросы к экзамену по дисциплине
1. Исследование операций как наука о принятии оптимальных решений.
2. Построение математической модели.
3. Математическое программирование. (Общий обзор, основные понятия, классы задач.)
4. Принятие решения: постановка задачи, возможные случаи.
5. Принятие решений в условиях риска. Критерий Байеса.
6. Принятие решений в условиях риска. Критерий Лапласа.
7. Принятие решений в условиях риска. Критерий Гермейера.
8. Принятие решений в условиях риска. Критерий Ходжа-Лемана.
9. Принятие решений в условиях неопределенности. Принцип максимина.
10. Принятие решений в условиях неопределенности. Критерий азартного игрока.
11. Принятие решений в условиях неопределенности. Критерий произведений.
12. Принятие решений в условиях неопределенности. Критерий Севиджа.
13. Принятие решений в условиях неопределенности. Критерий Гурвица.
14. Принятие решений в условиях противодействия. Общие понятия.
15. Матричные игры.
16. Чистые стратегии, седловая точка, цена игры.
17. Смешанные стратегии.
18. Представление матричной игры в виде задачи линейного программирования.
19. Графический метод решения матричной игры.
20. Принятие решений в условиях нескольких критериев выбора (многокритериальный выбор).
21. Линейные свёртки.
22. Максиминная и лексикографическая свёртки.
23. Мультипликативные свёртки.
24. Описание выбора на языке бинарных отношений.
25. Множество Парето. Максимальный элемент.
26. Матрицы смежности и инцидентности.
27. Принятие корпоративных решений.
28. Компетентность экспертов.
Контрольные экзаменационные вопросы используются в случае сдачи студентом экзамена по дисциплине на повышенную оценку в сравнении с оценкой, которую он получил по рейтингу полусеместра. В соответствии с действующим "Положением о кредитно-модульной системе организации учебного процесса и рейтинговом оценивании знаний студентов ЗГИА" оценка, которая получена на экзамене является окончательной и именно она вносится в экзаменационную ведомость и индивидуальный план (зачетную книжку) студента.
Учебно-методический материал по дисциплине
Основная литература (имеется в наличии в библиотеке ЗГИА)
1.Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие для вузов. - М.: Высшая школа , 1986. - 319 c.
2.Волков И.К., Загоруйко Е.А. Исследование операций: Учебник для втузов / Ред. Зарубин В.В., Крищенко А.П. - 2-е изд. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. - 435 c.
3.Евланов В.Г. Теория и практика принятия решений. – М.: Экономика, 1984. – 175 с.
4.Кини Р.Л., Райфа Х. Принятие решений при многих критериях: предпочтения и замещения. – М.: Радио и связь, 1981. – 560 с.
5.Колпаков В.М. Теория и практика принятия управленческих решений: Учеб. пособие для вузов. – К.: МАУП, 2000. – 254 с.
6.Костевич Л.С., Лапко А.А. Теория игр. Исследование операций: Учеб. пособие для вузов. - Мн.: Вышэйшая школа, 1982. - 230 c.
7.Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование: Учеб. пособие для вузов - М.: Высшая школа , 1976. - 350 c.
8.Мулен Э. Кооперативное принятие решений: Аксиомы и модели. - М.: Мир, 1991. - 463c.
9.Таха Хемди А. Введение в исследование операций, 7-е изд: Пер. с англ. – М.: Изд. дом "Вильямс", 2005. – 912 с.
10.Теория выбора и принятия решений Учеб. пособие для вузов. - М.: Наука, 1982. - 328 c.
11.Тоценко В.Г. Методы и системы поддержки принятия решений: Алгоритмический аспект / НАН Украины. Ин-т пробл. регистрации информ. - К.: Наук. думка, 2002. – 381 c.
12.Трухаев Р.И. Модели принятия решений в условиях неопределенности / АН СССР. Дальневост. науч. центр. Хабаров. комплекс НИИ. - М.: Наука, 1981. - 257 c.
Дополнительная литература
13.Вентцель Е.С. Исследование операций. – М.: Советское радио, 1972.
14.Гафт М.Г., Подиновский В.В. О построении решающих правил в задачах принятия решений. - Автоматика и телемеханика, №6, 1981.
15.Джексон П. Введение в экспертные системы: Пер. с англ.: Учеб. пособие. – М.: Изд. дом "Вильямс", 2001.
16.Ершов А.Т., Карандаев И.С., Статкус А.В. Матричные игры и графы. – М.: МИУ, 1986.
17.Ларичев О.И. Наука и искусство принятия решений. – М.: Наука, 1979.
18.Ларичев О.И. Теория и методы принятия решений, а также Хроника событий в Волшебных странах: Учебник. – М.: Логос, 2003.
19.Сигал И.Х., Иванова А.П. Введение в прикладное дискретное программирование: модели и вычислительные алгоритмы: Учеб. пособие. – М.: ФИЗМАТЛИТ, 2002. – 240с.
20.Фон Нейман Дж., Моргенштерн О. Теория игр и экономическое поведение. – М.: Наука, 1970.
21.Черноруцкий И.Г. Методы принятия решений. – СПб.: БХВ-Петербург, 2005. – 416 с.
Дата: 2019-07-31, просмотров: 299.