Максиминная свёртка – это самый простой способ построения обобщенного критерия (суперкритерия), основанный на применении уже хорошо нам известного принципа максимина.

Пусть мы имеем оценки некоторых объектов (альтернатив) по n критериям. Каждый из критериев имеет свою размерность, и эти размерности обычно не совпадают. Поэтому для начала нужно нормировать все имеющиеся оценки. Делается это с помощью нормирующих множителей – на основе исходной матрицы оценок строится новая матрица с такими элементами:

cij =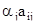

где aj = 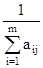 – нормирующие множители.

Далее к полученной матрице применяем принцип максимина. Посмотрим, как это делается на нашем примере:

Исходную матрицу мы, так же как и ранее, дополнили справа еще одним столбцом, в который внесли значения минимальных элементов каждой пересчитанной строки.

Из элементов добавленного столбца выбираем наибольший. Строка, в которой он стоит и будет оптимальной альтернативой. В данном случае оптимальной будет альтернатива А1.

Недостаток максиминной свёртки – это то, что она учитывает только те критерии, которые дают самые плохие оценки, все остальные критерии игнорируются. Из-за этого максиминную свёртку используют не слишком часто, чаще используют линейные и мультипликативные свёртки. Зато такой подход всегда дает гарантированный результат, ниже которого исхода не будет.

А что делать, если максиминная свёртка даст несколько одинаковых результатов (такое тоже бывает!), а ЛПР необходимо выбрать одно решение? Для такого интересного случая А. Джоффрион предложил использовать так называемую лексикографическую свёртку. Делается это так. Берутся две (или несколько) оптимальные альтернативы, полученные методом максиминной свёртки, и из них выбирается наилучшая методом линейной свёртки.

Как видим, с такими числовыми данными максиминная свёртка оптимальными считает альтернативы А1 и А2 . Теперь после максиминной свёртки применим к альтернативам А1 и А2 линейную свёртку:

В результате получили однозначный ответ: оптимальной является альтернатива А1 .

Мультипликативные свёртки

Рассмотрим мультипликативную свёртку с нормирующими множителями:

Z* = max ,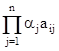

где aj – нормирующие множители.

Мультипликативная свёртка основывается на постулате: "низкая оценка хотя бы по одному критерию влечет за собой низкое значение функции полезности". Действительно, если вы выбираете торт, и он – несвежий, то это обстоятельство никак не может быть компенсировано его красотой или ценой.

Оптимальной стратегией снова является А3.

Посмотрим, какие результаты даст мультипликативная свёртка с весовыми коэффициентами:

Z* = max ,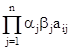

где aj – нормирующие множители,

вj – весовые коэффициенты.

Итоги отражены в таблице:

Оптимальной стратегией снова является А3.

В конце еще раз напомним непременное правило: перед тем, как применять какую-либо свёртку нужно автоматически всегда выделять множество Парето. И именно для множества Парето применять свёртки. Иначе вы или ваша программа будете выполнять лишнюю ненужную работу.