Групповая оценка объектов

В приведенном выше материале подразумевалось, что ЛПР – это некий эксперт-аналитик, принимающий решение по поставленной проблеме. А если проблемой занимаются несколько экспертов? А решение то должно быть одно! Такая задача называется задачей группового выбора или задачей принятия корпоративного решения.

Тут нужно отметить один важный психологический момент. Взрослого человека (начиная лет с 5-10) практически никогда невозможно заставить изменить свое мнение. (Есть, конечно, "безотказные" методы типа насилия, или денежного подкупа, но они к науке не имеют никакого отношения.) Поэтому эксперты в группе всегда будут:

- иметь разные мнения по поводу набора критериев, по которым надо оценивать альтернативные решения;

- иметь разные мнения о сравнительной значимости (весовых коэффициентах) критериев;

- давать разные оценки альтернатив по критериям;

- кроме этого эксперты будут иметь разную компетентность.

Исходя из таких очевидных фактов, можно с уверенностью утверждать, что у группы экспертов всегда должен быть руководитель.

Каждый из экспертов группы в принятии своего решения будет руководствоваться своим опытом и своими знаниями. Будем надеяться, что вышеприведенный материал окажет экспертам некую посильную помощь. Материал данного подраздела предназначен для руководителей групп экспертов, которые на основе всех решений группы обязаны приять единственное правильное решение.

Вспомним, как обычно преодолеваются групповые разногласия? В подавляющем большинстве случаев это делается с помощью обыкновенного голосования.

Рассмотрим формализованный пример голосования. В таблице начальных данных отражены количественные оценки четырёх альтернативных решений девятью экспертами:

Для начала необходимо найти множество Парето: это будут альтернативы А1, А2, А4. Оптимальное решение будем искать среди них. Для проведения голосования определим функцию полезности:

Z* = max ,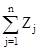

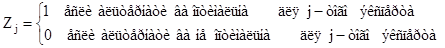
В последнем столбе таблицы размещены результаты голосования. Как видим, оптимальным решением является альтернатива А4 – за неё проголосовало пять экспертов из девяти – больше половины.

При всей простоте, широкой распространенности и многовековой исторической традиции использования метод голосования имеет один существенный недостаток. Голосование не считается с мнением меньшинства. Мнение меньшинства полностью игнорируется! Но иногда ведь случается, (правда очень редко) что именно среди этого меньшинства и находилось наилучшее решение! Кроме практического результата голосование наносит психологический удар по тем экспертам, мнения которых были отброшены. Математические методы принятия корпоративных решений стараются исправить этот недостаток. Учитываются мнения всех экспертов.

Рассмотрим такую функцию полезности с нормирующими множителями:

Z* = max ,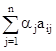

где aj =  .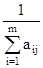

В этом случае оптимальным решением является альтернатива А1.

Заметим, что такой способ учитывает также и то, что эксперты пользовались разными шкалами оценок объектов.

А теперь попробуем учесть ещё и степень компетентности каждого эксперта. Функция полезности при этом будет выглядеть так:

Z* = max ,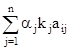

где aj – те же нормирующие множители,

kj – коэффициенты компетентности экспертов.

Ниже будет рассмотрен один из способов определения коэффициентов компетентности экспертов.

А пока рассмотрим ту же задачу с уже якобы вычисленными коэффициентами компетентности экспертов. В таблице снова сначала – условие, ниже – результаты:

А теперь мы получили в качестве оптимальной альтернативу А2.

Надо отметить, что приведенные два последних способа принятия группового решения годятся только для согласованных суждений экспертов. Согласованность – это степень расхождения мнений экспертов. Методика вычисления согласованности оценок экспертов достаточно сложна. По необходимости с ней можно ознакомиться в специальной литературе по принятию корпоративных решений.

Если эксперты честно оценивают реальный объект, то их оценки не должны сильно расходиться. Если же они все-таки существенно расходятся, то можно получить часто упоминаемую в литературе так называемую "среднюю температуру по больнице". Действительно, если сложить температуру всех высокотемпературных больных и температуру тел в морге, а потом поделить на общее количество замеров, то можно получить 36,6°. Свидетельствует ли это о том, что "в среднем" все находящиеся в больнице здоровы?

Если согласованность оказалась низкой, то нужно пытаться выяснить причину расхождений и по возможности попытаться устранить её. Часто причиной может быть отсутствие важной информации у некоторых экспертов. В некоторых случаях эксперты разбиваются на две устойчивые группы. Группы нужно уметь выявлять и обрабатывать отдельно.