Постановка задачи

Если платежная матрица не имеет седловой точки, то 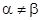 . А значит  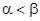. Такая игра в чистых стратегиях не разрешима. Первый игрок в таком случае будет стремиться увеличить свой выигрыш, а второй – уменьшить свой проигрыш. Поиск такого решения приводит к применению сложной стратегии, состоящей в случайном применении двух и более чистых стратегий с определенными вероятностями:

PA = (p1, p2, …, pm) где pi – это вероятности применения чистых стратегий игроком А;

QB = (q1, q2, …, qn) где qj – это вероятности применения чистых стратегий игроком B;

при этом 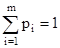 и  .

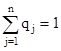Такие наборы вероятностей применения чистых стратегий игроками А и В называются смешанными стратегиями.

Заметим, что чистые стратегии – это частный случай смешанных стратегий. Например, чистая стратегия первого игрока – это смешанная стратегия, у которой все вероятности pi = 0 , кроме соответствующего номера k чистой стратегии: pk = 1 .

Основная теорема теории игр (Теорема фон-Неймана): любая конечная игра двух лиц с нулевой суммой разрешима в смешанных стратегиях.

Как же искать смешанные стратегии? Их можно найти точно – алгебраическим способом (в частности, с помощью симплекс-метода) или графическим способом (для игры размерности 2 х n или m х 2 ).

Для того чтобы точно найти решение матричной игры в смешанных стратегиях, нужно представить заданную матричную игру в виде задачи линейного программирования и решить её симплекс-методом.

Рассмотрим матричную игру, не разрешимую в чистых стратегиях, в общем виде:

Заметим, что в матричной игре, разрешимой в чистых стратегиях, элементы платежной матрицы могут быть как положительными, так и отрицательными. Для симплекс-метода, которым будем решать игру, не разрешимую в чистых стратегиях, необходимо, чтобы элементы платежной матрицы были неотрицательными. Для этого, если в платежной матрице будут отрицательные элементы, нужно ко всем элементам платежной матрицы прибавить достаточно большое число с . При этом решение задачи не изменится, а цена игры увеличится на с.#

PA = (p1, p2, …, pm)– это оптимальная смешанная стратегия первого игрока. Её применение гарантирует первому игроку выигрыш не меньший, чем цена игры n . Если при этом второй игрок выберет стратегию В1, математически все вышесказанное будет иметь вид:

а11р1 + а21р2 + … + am1pm ≥ n

Таких неравенств будет столько, сколько есть возможных альтернатив у второго игрока, т.е. столбцов платежной матрицы – n штук:

а11р1 + а21р2 + … + am1pm ≥ n

а12р1 + а22р2 + … + am2pm ≥ n

а1nр1 + а2nр2 + … + amnpm ≥ n

Разделив все неравенства на n , получим (в общем виде):

а1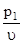j  + а2j 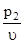 + … + amj  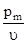≥ 1

Обозначим: 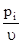 = xi, . С помощью таких новых переменных вышеуказанные неравенства запишутся в виде:

а11 x1 + а21 x2 + … + am1 xm ≥ 1

а12 x1 + а22 x2 + … + am2 xm ≥ 1

а1n x1 + а2n x2 + … + amn xm ≥ 1

Просуммируем новые переменные:

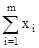 = x1 + x2 + … + xm =  +  + … +  =  =

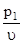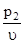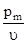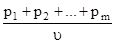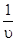
PA = (p1, p2, …, pm)– это оптимальная смешанная стратегия первого игрока. То есть нужно так подобрать (p1, p2, …, pm) , чтобы n была как можно большей. Или же, что то же самое, чтобы 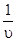 была как можно меньшей.

Таким образом, используя новые переменные и учитывая всё вышесказанное, исходную матричную игру можно представить в виде задачи линейного программирования:

найти вектор переменных Х = {x1, x2, … , xm}, такой что:

целевая функция f = 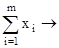 min

при множестве ограничений:

АТХ ≥ Е

гдеА – матрица коэффициентов (платежная матрица), заданная в условии;

Е – единичный вектор

Х – вектор неизвестных переменных, такой что xi =  ;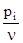

n – это цена игры:n =  =  ;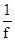

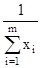рi – это коэффициенты вектора смешанной стратегии первого игрока.