Рассмотрим числовой пример.
Пусть имеем игру с платежной матрицей:
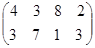
Проверим, имеет ли наша матричная игра седловую точку? Для этого используем принцип максимина.
Выигрыш игрока А:a = 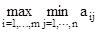 = 2 он достигается в первой строке.
= 2 он достигается в первой строке.
Выигрыш игрока В:в = 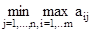 = 3 он достигается в четвертом столбце.
= 3 он достигается в четвертом столбце.
Как видим, выигрыши игроков не совпадают, значит у матрицы нет седловой точки. Значит, нужно искать смешанные стратегии.
В данном конкретном случае в множестве ограничений будет четыре неравенства (т.к. в условии задачи четыре столбца). Пересчитывать симплекс- таблицы с четырьмя строками не очень сильно хочется, поэтому удобнее решить двойственную задачу (для коэффициентов вектора смешанной стратегии второго игрока), в которой будет всего две строки (т.к. в условии задачи две строки):
найти вектор двойственных переменных Y = {y1, y2, … yn}, такой что:
целевая функция g = 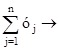 max
max
при множестве ограничений:АY ≤ Е
Для нашего примера задача линейного программирования будет такой:
найти вектор Y = {y1, y2, y3, y4}, такой что:
целевая функция g = 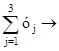 max
max
при множестве ограничений:
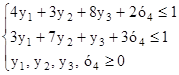
Далее нужно вспомнить методику применения симплекс-метода и использовать её для нашей задачи.
Однако, как показывает многолетняя практика, студенты обладают так называемой "краткосрочной памятью", которая работает только до сдачи необходимого экзамена. Поэтому вспомнить сейчас методику применения симплекс-метода вряд ли кто-то сможет. Для этого нужно сходить в библиотеку, найти специальную литературу и умело ей воспользоваться. Осмелимся заметить, что и этого половина студентов сделать поленится и благополучно завалит данную тему J . #
Поэтому для всеобщего блага приведем здесь методику применения симплекс-метода (пройденного и успешно сданного в математическом программировании) для нашей конкретной задачи.
1 этап – приведение задачи линейного программирования к каноническому виду.
Неравенства во множестве ограничений нужно превратить в равенства с помощью добавления искусственных переменных. Для того чтобы неравенства превратить в равенства, надо в каждое неравенство добавить (или отнять – в зависимости от знака неравенства) искусственную переменную:
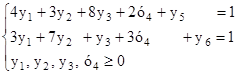
Целевая функция при этом будет выглядеть так:g = y1 + y2 + y3 + y4 + 0y5 + 0y6
2 этап – определение начального опорного плана.
В полученном случае начальный опорный план будут составлять искусственные переменные, входящие в ограничения с коэффициентами +1 :{ y5 ; y6 }. Новых искусственных переменных для данной задачи вводить не требуется.
3 этап – заполнение исходной симплекс-таблицы.
Исходная симплекс-таблица для нашей двойственной задачи будет иметь вид:
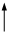 В столбец "текущий базис" ставим переменные, начального опорного плана : { y5 ; y6 }.
В столбец "текущий базис" ставим переменные, начального опорного плана : { y5 ; y6 }.
В столбец "сi" ставим их коэффициенты в целевой функции.
В столбец "А0" ставим вектор ограничений Е : а10 = 1 ;а20 = 1 .
В самую верхнюю строку таблицы ставим коэффициенты cj при соответствующих переменных в целевой функции:c1 = 1 ; c2 = 1 ; c3 = 1 ; c4 = 1 ; c5 = 0 ; c6 = 0 .
В столбцы "А1", ...., "А6" ставим соответствующие коэффициенты матрицы ограничений А.
Вычисляем оценки по формулам
D0 = 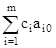 ; .Dj =
; .Dj = 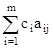 cj
cj
и ставим их в самую нижнюю строку симплекс-таблицы (строку оценок) :
D0 = 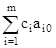 = 0 * 1 + 0 * 1 = 0D1 =
= 0 * 1 + 0 * 1 = 0D1 = 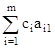 c1 = 0 * 4 + 0 * 3 1 = 1
c1 = 0 * 4 + 0 * 3 1 = 1
D2 = 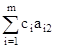 c2 = 0 * 3 + 0 * 7 1 = 1D3 =
c2 = 0 * 3 + 0 * 7 1 = 1D3 = 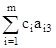 c3 = 0 * 8 + 0 * 1 1 = 1
c3 = 0 * 8 + 0 * 1 1 = 1
D4 = 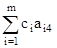 c4 = 0 * 2 + 0 * 3 1 = 1D5 =
c4 = 0 * 2 + 0 * 3 1 = 1D5 = 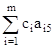 c5 = 0 * 1 + 0 * 0 0 = 0
c5 = 0 * 1 + 0 * 0 0 = 0
D6 = 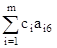 c6 = 0 * 0 + 0 * 1 0 = 0
c6 = 0 * 0 + 0 * 1 0 = 0
4 этап – пересчет симплекс-таблицы.
1. Если j ³ 0 для всех j = 1, 2, .... , n , то данный план (в столбце "текущий базис") – оптимален. В нашем случае это условие не выполняется, значит, текущий базис можно улучшить.
2. Если имеются k < и в столбце Аk все элементы aik 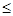 0 , то целевая функция не ограничена сверху на допустимом множестве и данная задача не имеет смысла. В нашем случае видим, что целевая функция сверху ограничена.
0 , то целевая функция не ограничена сверху на допустимом множестве и данная задача не имеет смысла. В нашем случае видим, что целевая функция сверху ограничена.
3. Если имеются j < и в столбцах Аj , соответствующих этим оценкам, существует хотя бы один элемент aik > 0, то возможен переход к новому лучшему плану, связанному с большим значением целевой функции. У нас так и есть.
4. Переменная хk, которую необходимо ввести в базис, для улучшения плана соответствует наименьшей отрицательной оценке j. Столбец Ak, содержащий эту оценку называется ведущим. В нашем случае все оценки одинаковы. Поэтому в качестве ведущего столбца выберем любую оценку, например, третью: k = 3.
5. Ищем min{ ai0 / ai1 } = min{ 1/8 ; 1/1 } = 1/8– этот минимум достигается при i = 1. Значит, r = 1первая строка – ведущая. (на рисунке помечена стрелкой)
Ведущий элементark = a13 = 8 (на рисунке выделен)
6. Заполняем новую симплекс-таблицу.
В столбец "текущий базис" вместо переменной у5 ставим переменную у3 .
В столбец "сi" ставим коэффициент переменной у3 в целевой функции.
Самая верхняя строка таблицы всегда остаётся неизменной.
Пересчитываем ведущую строку по формуле 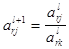 :
:
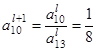
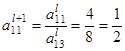
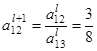
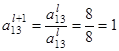
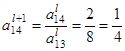
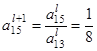
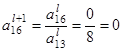
После этого пересчитываем остальные строки по формуле
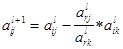 :
:
вторая строка (i = 2)
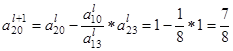
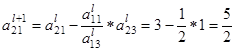
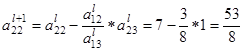
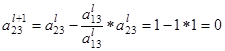
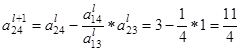
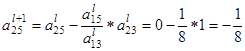
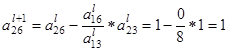
Пересчитываем и заполняем строку оценок:
D0 = 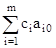 = 1 *
= 1 * 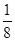 + 0 *
+ 0 * 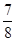 =
= 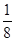 D1 =
D1 = 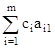 c1 = 1 *
c1 = 1 * 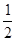 + 0 *
+ 0 * 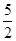 1 =
1 = 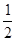
D2 = 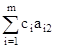 c2 = 1 *
c2 = 1 * 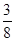 + 0 *
+ 0 * 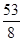 1 =
1 = 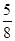 D3 =
D3 = 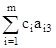 c3 = 1 * 1 + 0 * 0 1 = 0
c3 = 1 * 1 + 0 * 0 1 = 0
D4 = 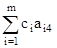 c4 = 1 *
c4 = 1 * 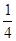 + 0 *
+ 0 * 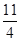 1 =
1 = 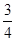
D5 = 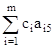 c5 = 1 *
c5 = 1 * 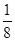 + 0 *
+ 0 * 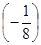 0 =
0 = 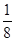 D6 =
D6 = 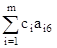 c6 = 1 * 0 + 0 * 1 0 = 0
c6 = 1 * 0 + 0 * 1 0 = 0
После этого повторяем 4 этап до тех пор, пока не будет выполнен п.1 (все j ³ 0).
В нашем случае имеются j < и наименьшая среди них 4 . Значит ведущим столбцом на данном шаге будет A4 (пометим его стрелкой).
Ищем min{ ai0 / ai4 } = min{ 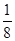 :
: 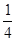 ;
; 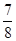 :
: 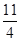 } = min{
} = min{ 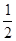 ;
; 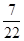 } =
} = 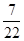 – этот минимум достигается при i = 2. Значит, r = 2вторая строка – ведущая (на рисунке помечена стрелкой).
– этот минимум достигается при i = 2. Значит, r = 2вторая строка – ведущая (на рисунке помечена стрелкой).
Таким образом, в новый текущий базис вместо переменной у6 надо ввести переменную у4 .
Пересчитываем все элементы новой симплекс-таблицы.
Пересчитываем ведущую строку (вторую):
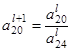 =
= 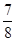 :
: 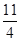 =
= 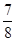
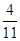 =
= 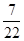
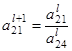 =
= 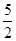 :
: 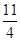 =
= 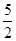
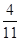 =
= 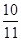
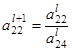 =
= 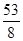 :
: 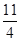 =
= 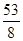
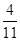 =
= 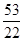
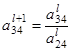 = 0 :
= 0 : 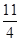 = 0
= 0
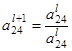 =
= 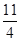 :
: 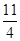 = 1
= 1 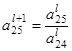 = –
= – 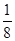 :
: 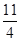 = –
= – 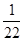
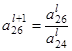 = 1 :
= 1 : 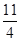 =
= 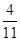
Приведенные выше и ниже вычисления представлены в весьма подробном виде. Это сделано из тех соображений, что как опять таки показывает практика, даже не смотря на достаточно хорошее понимание и усвоение теоретического материала, ошибки зачастую возникают именно при выполнении элементарных арифметических операций. Не следует думать, что средняя школа осталась позади, и вы всё можете посчитать в уме. Поэтому всем студентам мы советуем не лениться и подробно расписывать все арифметические действия (особенно с дробями).#
Пересчитываем оставшуюся строку (первую):
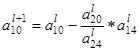 =
= 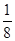 –
– 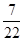
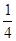 =
= 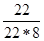 –
– 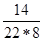 =
= 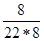 =
= 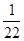
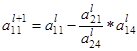 =
= 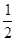 –
– 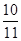
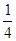 =
= 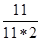 –
– 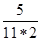 =
= 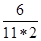 =
= 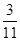
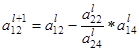 =
= 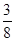 –
– 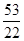
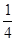 =
= 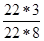 –
– 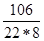 = –
= – 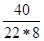 = –
= – 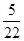
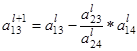 = 1 – 0
= 1 – 0 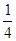 = 1
= 1 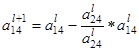 =
= 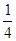 –
– 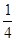 = 0
= 0
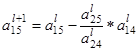 =
= 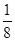 –
– 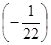
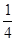 =
= 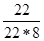 +
+ 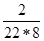 =
= 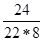 =
= 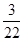
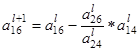 = 0 –
= 0 – 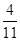
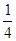 = –
= – 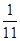
Пересчитываем и заполняем строку оценок:
D0 = 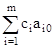 = 1 *
= 1 * 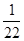 + 1 *
+ 1 * 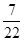 =
= 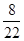 =
= 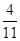
D1 = 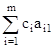 c1 = 1 *
c1 = 1 * 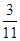 + 1 *
+ 1 * 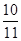 1 =
1 = 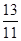
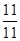 =
= 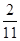
D2 = 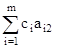 c2 = 1 *
c2 = 1 * 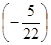 + 1 *
+ 1 * 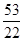 1 =
1 = 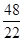
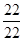 =
= 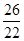 =
= 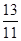
D3 = 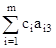 c3 = 1 * 1 + 1 * 0 1 = 0
c3 = 1 * 1 + 1 * 0 1 = 0
D4 = 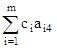 c4 = 1 * 0 + 1 * 1 1 = 0
c4 = 1 * 0 + 1 * 1 1 = 0
D5 = 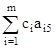 c5 = 1 *
c5 = 1 * 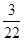 + 1 *
+ 1 * 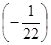 0 =
0 = 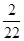 =
= 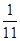
D6 = 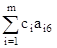 – c6 = 1
– c6 = 1 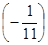 + 1
+ 1 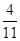 – 0 =
– 0 = 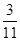
Повторяем 4-й этап. При проверке п. 1 видим, что все j ³ 0 . Следовательно, данный план {у3, у4} (в столбце "текущий базис") – оптимален. Больше пересчитывать симплекс-таблицу не нужно.
Решение задачи линейного программирования полностью содержится в последней симплекс-таблице.
Значения переменных находятся в столбце А0 возле соответствующих переменных. В нашем случае, мы видим, что у3 = 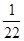 , у4 =
, у4 = 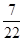 . Переменные у1 и у2 не входят в базис, поэтому их значения будут равны нулю. Таким образом, вектор переменных будет выглядеть так: Y =
. Переменные у1 и у2 не входят в базис, поэтому их значения будут равны нулю. Таким образом, вектор переменных будет выглядеть так: Y = 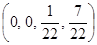 .
.
Значение целевой функции – это значение оценки . В нашем случае g = = 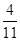 .
.
Значения двойственных переменных находятся в строке оценок возле искусственных переменных. В нашем случае это 5 и 6 , то есть х1 = 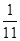 , х2 =
, х2 = 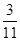 . Таким образом, вектор двойственных переменных будет выглядеть так:Х =
. Таким образом, вектор двойственных переменных будет выглядеть так:Х = 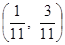 .
.
Итак, мы получили решение прямой задачи (которая у нас была двойственной): Y = 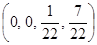
и двойственной задачи к данной (которая у нас была прямой):
Х = 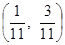
Значения целевых функций при этом будут совпадать:f = g = 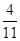 .
.
Найдем цену игры:n = 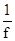 =
= 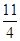
Далее найдем коэффициенты смешанной стратегии
для первого игрока по формуле рi = 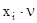 :
:
Р = 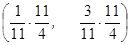 =
= 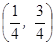 ,
,
для второго игрока по формуле qi = 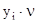 :
:
Q = 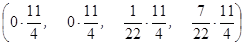 =
= 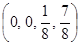 .
.
Особо "продвинутые" студенты при нахождении решения задачи линейного программирования, чтобы не считать симплекс-метод вручную академическим способом, могут воспользоваться средствами MS Excel. Это гораздо быстрее и удобнее.#
Ответ: смешанная стратегия для первого игрока Р = 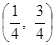 ,
,
смешанная стратегия для второго игрока Q = 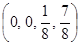 ,
,
цена игры n = 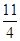 .
.
Дата: 2019-07-31, просмотров: 285.