Рассмотрим парную конечную антагонистическую игру. Пусть игрок А располагает m личными стратегиями, которые обозначим А1, а2 ..., Аm. Пусть у игрока В имеется n личных стратегий, обозначим их В1, В2, ,.., Вn. Говорят, что игра имеет размерность m х n . В результате выбора игроками любой пары стратегий Аi и Вj (i = 1,2 …, m; j = 1,2, …, n).

Однозначно определяется исход игры, т.е. выигрыш аij игрока А (положительный или отрицательный) и проигрыш (-аij) игрока В . Предположим, что значения аij известны для любой пары стратегий (Аi Вj). Значения этих выигрышей заданы в платежной матрице

Строки этой таблицы соответствуют стратегиям игрока А , а столбцы – стратегиям игрока В .

С помощью хорошо нам знакомого принципа максимина найдем гарантированный наибольший выигрыш для игрока А:

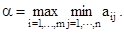
Найденное число a называется нижней ценой игры.

Стратегия, соответствующая максимину, называется максиминной стратегией – она будет оптимальной стратегией игрока А.

Посмотрим на эту ситуацию с точки зрения второго игрока: ему необходимо уменьшить свои потери. В таком случае критерию максимина превратится в минимаксный и гарантированный наименьший проигрыш для игрока В будет таким:

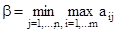
Найденное число в называется верхней ценой игры

Стратегия, соответствующая минимаксу, называется минимаксной стратегией – она будет оптимальной стратегией игрока В.

Причем, для нижней и верхней цены игры всегда справедливо неравенство:

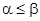
Если нижняя и верхняя цены игры совпадают, то общее значение верхней и нижней цены игры a = в = n называется чистой ценой игры, или ценой игры. Элемент платежной матрицы, в котором достигается чистая цена игры, называется седловой точкой (по аналогии с поверхностью седла, которая искривляется вверх в одном направлении и вниз – в другом). Найденные оптимальные стратегии игроков А и В в данном случае называются чистыми стратегиями.

Матричная игра с платежной матрицей, имеющей седловую точку, называется игрой, разрешимой в чистых стратегиях. При этом очевидно, что решение игры обладает устойчивостью, т.е. если один из игроков придерживается своей оптимальной стратегии, то для другого не может быть выгодным отклоняться от своей оптимальной стратегии. Оба игрока находятся в "положении равновесия", из которого не выгодно выходить каждому.

Рассмотрим числовой пример.

Пусть имеем игру с платежной матрицей:

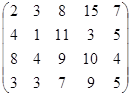
Проверим, имеет ли наша матричная игра седловую точку? Для этого используем принцип максимина.

Дополним исходную матрицу справа еще одним столбцом, а снизу – еще одной строкой. В них будем заносить значения минимальных элементов каждой строки и значения максимальных элементов каждого столбца соответственно:

Найдем нижнюю цену игры. Выигрыш игрока А:

a = 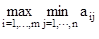 = 4он достигается в третьей строке.

Найдем верхнюю цену игры. Выигрыш игрока В:

в = 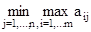 = 4 он достигается во втором столбце.

Как видим, выигрыши игроков совпадают: a = в = n = 4 , значит у матрицы имеется седловая точка. А значит, у данной матричной игры имеется пара оптимальных чистых стратегий А3В2 . Цена игры n = 4.

Но такое бывает далеко не всегда.