5.1 Постановка задачи, основные понятия

Все перечисленные классические критерии выбора не охватывают всевозможные практические ситуации. К каждой конкретной практической ситуации ЛПР может выработать свой "новый" критерий, который будет более точно количественно и качественно описывать данную ситуацию.

К сожалению или счастью, жизнь устроена несколько сложнее и достаточно часто бывает невозможно описать ситуацию одним критерием. Даже в обыденной жизни мы практически никогда не используем единственный критерий, например, при выборе подарка ко дню рождения, или при выборе блюд из меню в кафе, или при выборе места, куда поехать в отпуск.

А представьте, что вы – проектировщик баз данных. В таком случае при выборе оптимального проекта баз данных вам следует учитывать тоже несколько критериев: объем занимаемой оперативной памяти, средняя скорость одной операции, размер программного кода, аппаратные требования, обучаемость обслуживающего персонала, возможность и стоимость сопровождения и прочие. Ниже будут рассматриваться прикладные задачи с уже изученными нами критериями: Байеса, Лапласа и др. Но если вы все-таки – например, проектировщик баз данных, то вам надо будет вместо них рассматривать "свои" критерии, которые являются спецификой вашего рода деятельности.

Такие ситуации описываются многокритериальными задачами принятия решений.

Теоретически можно представить себе случай, когда в допустимом множестве альтернатив существует одна альтернатива, которая лучше всех по всем критериям сразу. Очевидно, что она и будет лучшей.

Однако на практике такое бывает не всегда. Для решения таких задач разработаны специальные методы. Надо сказать, что данное научное направление сравнительно ново – оно развивается последние 30 – 40 лет. Уже известные методы корректируются, обобщаются, разрабатываются новые. Приятно отметить, что одним из основоположников и всемирно признанным гуру данного научного направления является наш почти соотечественник В.В. Подиновский.

Рассмотрим приведенный выше числовой пример. И применим к нему все изученные нами критерии. Результаты отобразим в таблице:

Заметим, что стратегия (альтернатива) А4 по всем девяти критериям хуже, чем любая другая стратегия. Её можно убрать из рассмотрения, при этом результат выбора не изменится. Это утверждает принцип Парето. Оставшиеся альтернативы А1, А2, А3, будут образовывать множество Парето для данной задачи.

Из допустимого множества альтернатив множество Парето образуют те альтернативы, каждая из которых не хуже по всем критериям, чем любая альтернатива, не вошедшая во множество Парето, а хотя бы по одному критерию – лучше.

Согласно принципу Парето оптимальная альтернатива содержится во множестве Парето. Если, например исходная задача содержит 100 альтернативных решений, а множество Парето состоит из 20 альтернатив, то применение принципа Парето в 5 раз уменьшает размерность задачи, соответственно в 5 раз увеличится скорость работы программы, реализующей решение такой задачи!

Далее полученную многокритериальную задачу принятия решения на множестве Парето можно свести к однокритериальной, введя некий обобщенный критерий Z* как функцию от предыдущих частных критериев. Обобщенный критерий Z* в литературе еще называют функцией полезности. Процесс сведения многокритериальной задачи к однокритериальной называется свёрткой.

Линейные свёртки

Начнем с линейных свёрток. Все линейные свёртки основываются на принципе: "низкая оценка по одному критерию может быть компенсирована высокой оценкой по другому".

Рассмотрим простую линейную аддитивную свёртку:

Z* = max ,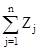

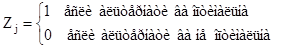
То есть, данная свёртка подсчитывает, сколько раз та или иная стратегия была оптимальной. Результаты отобразим в таблице:

В последнем столбе таблицы размещены результаты свёртки. Как видим, оптимальной стратегией является А3.

Такая свёртка является самой простой из линейных, она не учитывает количественных показателей значений критериев.

Рассмотрим линейную аддитивную свёртку с нормирующими множителями:

Z* = max ,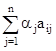

где aj = 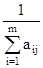 – нормирующие множители.

Как видим, оптимальной стратегией также является А3. Но в этом случае уже нет такого количественного отрыва как в предыдущей простой линейной свёртке. Да и стратегия А2 уже не кажется очень сильно плохой. Если бы были чуть другие начальные данные, то ответы двух рассмотренных вариантов свёрток могли бы и не совпасть.

Линейная аддитивная свёртка с нормирующими множителями позволяет работать с количественными критериями, имеющими, как в нашем случае, разные единицы измерений.

Рассмотрим линейную аддитивную свёртку с весовыми коэффициентами:

Z* = max ,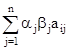

где aj – те же нормирующие множители,

вj – весовые коэффициенты, отражающие относительный
вклад частных критериев в общий критерий.

Весовые коэффициенты принято указывать уже нормированными величинами (Sвj = 1).

Очевидно, что в каждой отдельной конкретной ситуации частные критерии по-разному влияют на общий суперкритерий. Поэтому естественно им придать в общей формуле разный удельный вес. Это можно сделать с помощью весовых коэффициентов. Но где же их взять? Обычно ЛПР сам назначает каждому критерию весовые коэффициенты на свой "мудрый" взгляд. На этом этапе строгая математическая наука заканчивается – конечный результат лежит целиком на совести ЛПР и зависит от его опыта и интуиции в данной сфере. Однако от такого субъективизма никуда не денешься – нельзя же всю жизнь формализовать с помощью математических формул!

Как видим, при неизменном условии задачи оптимальной получилась стратегия А2, хотя в двух предыдущих свёртках она "пасла задних". Все дело в весовых коэффициентах!