Основные понятия и формулы
Тепловое излучение - равновесное излучение электро-магнитных волн нагретыми телами.
· Закон Стефана-Больцмана:
для черного тела
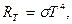
где R Т – энергетическая светимость черного тела; T– термодинамическая температура черного тела; s – постоянная Стефана-Больцмана;
для нечерного тела
R Т = a Т s T4
где a Т – коэффициент, зависящий от природы тела и от температуры.
· Закон смещения Вина
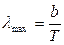 ,
,
где lmax – длина волны, соответствующая максимуму спектральной плотности энергетической светимости черного тела.
Фотоны — квазичастицы (кванты света)
· Энергия фотона
e = h n,
где h – постоянная Планка; n – частота света.
· Импульс фотона
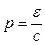 .
.
· Уравнение Эйнштейна для внешнего фотоэффекта
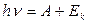 ,
,
где А – работа выхода электрона из металла; Ек – максимальная кинетическая энергия вылетевшего электрона.
· Изменение длины волны при эффекте Комптона
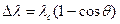 ,
,
где 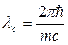 – комптоновская длина волны, (m – масса покоя рассеивающей частицы);
– комптоновская длина волны, (m – масса покоя рассеивающей частицы); 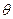 – угол рассеяния фотона.
– угол рассеяния фотона.
Методические указания и примеры решения задач
Задачи на тепловое излучение решаются с применением законов Стефана-Больцмана и Вина.
При решении задач на световые кванты учитываются, что взаимодействие фотонов с веществом подчиняются законам сохранения энергии и импульса. Закон сохранения энергии, записанный для взаимодействия фотона с электронами вещества при внешнем фотоэффекте, дает формула Эйнштейна. Применение к указанному взаимодействию закона сохранения импульса приводит к формуле, определяющей давление светового излучения, а применение обоих законов сохранения – к формуле Комптона для изменения длины волны света при его рассеянии на электронах.
Пример 2.15 При нагревании черного тела длина волны, соответствующая максимуму его спектральной плотности энергетической светимости, изменилась на 0,5 мкм. До какой температуры нагрелось тело? Начальная температура 127ºС.
Дано: 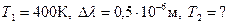
Решение
В соответствии с законом смещения Вина при увеличении температуры тела его 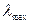 уменьшается. Следовательно, можно записать для двух температур Т1 и
уменьшается. Следовательно, можно записать для двух температур Т1 и 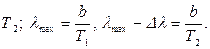 Вычитая второе равенство из первого, находим
Вычитая второе равенство из первого, находим 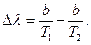 Откуда
Откуда 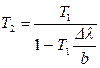 . Учитывая, что постоянная Вина
. Учитывая, что постоянная Вина 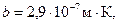 получим
получим
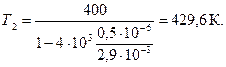
Пример 2.16 Определить длину волны рентгеновского излучения, если при комптоновском рассеянии этого излучения под углом θ = = 60о длина волны рассеянного излучения оказалась равной 57 пм.
Дано: λ′ =57 пм, θ = 60о, λ = ?
Решение
Для определения длины волны падающего фотона воспользуемся формулой Комптона
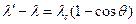 ,
,
где 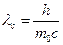 – комптоновская длина волны, θ – угол отклонения рентгеновского фотона от первоначального нправления движения. Для электрона
– комптоновская длина волны, θ – угол отклонения рентгеновского фотона от первоначального нправления движения. Для электрона 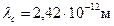 . Тогда
. Тогда
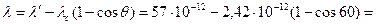
= 55,79 пм
Таким образом, после рассеяния на свободном электроне длина волны фотона увеличивается. Величина изменения длины волны определяется углом рассеяния 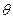 .
.
Пример 2.17. Фотоэлектроны, вырываемые с поверхности металла светом с длиной волны λ = 400 нм, полностью задерживаются обратным напряжением Uз = 1,2 В. Определить красную границу фотоэффекта.
Дано: λ =400 нм, Uз = 1,2 В; λо =?
Решение
Из условия задачи известны длина волны падающего света и задерживающее напряжение тормозящего электрического поля. Другими словами, согласно теории фотоэффекта, задана энергия светового фотона 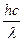 и максимальная кинетическая энергия фотоэлектронов
и максимальная кинетическая энергия фотоэлектронов 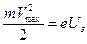 . Эти данные позволяют, воспользовавшись законом сохранения энергии, найти работу выхода фотоэлектрона из металла
. Эти данные позволяют, воспользовавшись законом сохранения энергии, найти работу выхода фотоэлектрона из металла 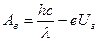 , которая, как известно, полностью определяет красную границу фотоэффекта λо:
, которая, как известно, полностью определяет красную границу фотоэффекта λо:
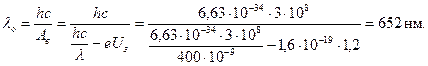
Поскольку красная граница фотоэффекта зависит только от химической природы металла, то величина λ о позволяет по таблицам (см. приложение) определить материал катода фотоэлемента.
Элементы квантовой механики
Основные понятия и формулы
· Длина волны де Бройля
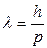 ,
,
где р – импульса частица.
· Соотношение неопределенностей Гейзенберга
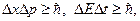
где Δх – неопределенность координаты; Δр – неопреде-ленность импульса; ΔЕ – неопределенность энергии; Δt – неопределенность времени.
Методические указания и примеры решения задач
Пример 2.18 Найти длину волны де Бройля для электрона, обладающего кинетической энергией: 1) Т = 100 эВ; 2) Т =3 МэВ.
Дано: Т =100 эВ; Т =3 МэВ; λ =?
Решение
Поскольку длина волны де Бройля 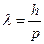 , то задача сводится к выражению импульса p электрона через его кинетическую энергию Т. Решение задачи зависит от того, классической или релятивистской частицей следует считать электрон.
, то задача сводится к выражению импульса p электрона через его кинетическую энергию Т. Решение задачи зависит от того, классической или релятивистской частицей следует считать электрон.
1.В первом случае Т << moc2, где moc2 =0,51 МэВ – энергия покоя электрона, то электрон является классической частицей, его импульс и кинетическая энергия связаны соотношением: 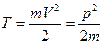 . Отсюда
. Отсюда 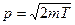 , подставив его в формулу длины волны де Бройля, получим:
, подставив его в формулу длины волны де Бройля, получим:
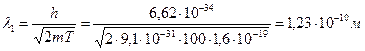 .
.
2.Во втором случае 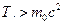 , поэтому электрон следует считать релятивистской частицей, для которой импульс и энергия связаны:
, поэтому электрон следует считать релятивистской частицей, для которой импульс и энергия связаны:
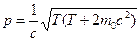 . Тогда для дебройлевской длины волны получим выражение:
. Тогда для дебройлевской длины волны получим выражение:
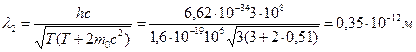
Пример 2.19 Электрон с кинетической энергией Т= 4 эВ локализован в области размером l=1 мкм. Оценить с помощью соотношения неопределенностей относительную неопределенность его скорости.
Дано: Т= 4 эВ= 4·1,6·10-19 = 6,4·10-19 Дж, l=10-6 м.
Решение
Полагая в соотношении неопределенностей 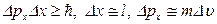 , получаем для неопределен-ности модуля скорости электрона формулу
, получаем для неопределен-ности модуля скорости электрона формулу 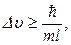 где m – масса электрона. Учитывая, что по условию задачи
где m – масса электрона. Учитывая, что по условию задачи 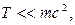 находим
находим 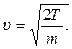 Таким образом, для относительной неопределенности модуля скорости электрона получаем оценку
Таким образом, для относительной неопределенности модуля скорости электрона получаем оценку 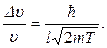 Подставляя численные значения величин, находим
Подставляя численные значения величин, находим 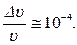
Дата: 2019-07-30, просмотров: 308.