Основные понятия и формулы
• Закон Ампера
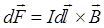 или
или 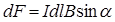 ,
,
где 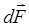 сила, действующая на элемент тока
сила, действующая на элемент тока 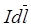 , помещенный в магнитное ноле с индукцией
, помещенный в магнитное ноле с индукцией 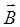 ;
; 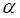 – угол между направлениями поля и тока.
– угол между направлениями поля и тока.
• Магнитный момент контура с током
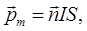
где 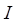 – сила тока в контуре;
– сила тока в контуре; 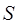 – площадь, охватываемая контуром;
– площадь, охватываемая контуром; 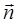 – единичный вектор нормали к поверхности
– единичный вектор нормали к поверхности 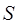 , ограниченной контуром с током (направление
, ограниченной контуром с током (направление 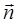 определяется по правилу буравчика).
определяется по правилу буравчика).
• Вращательный момент, действующий на контур с током, помещенный в магнитное поле,
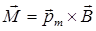 , или
, или 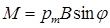 ,
,
где 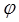 – угол между векторами
– угол между векторами 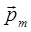 и
и 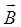 .
.
• Сила 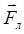 , действующая на заряд q, движущийся со скоростью
, действующая на заряд q, движущийся со скоростью 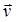 в магнитном поле (сила Лоренца),
в магнитном поле (сила Лоренца),
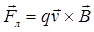 , или
, или 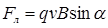 ,
,
где 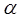 – угол между векторами
– угол между векторами 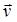 и
и 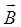 .
.
• Поток вектора магнитной индукции 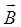 (магнитный поток);
(магнитный поток);
а) в случае произвольной поверхности S и неоднородного поля 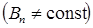
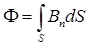 ,
,
где 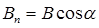 - проекция вектора
- проекция вектора 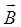 на направление нормали
на направление нормали 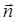 к элементу поверхности dS (
к элементу поверхности dS ( 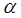 – угол между векторами
– угол между векторами 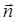 и
и 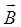 );
);
б) в случае однородного поля и плоской поверхности, расположенной перпендикулярно вектору 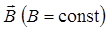 ,
,
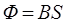 .
.
• Полный поток магнитной индукции, сцепленный с витками контура (потокосцепление),
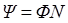 ,
,
где 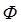 – магнитный поток через один виток;
– магнитный поток через один виток; 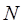 – число витков контура.
– число витков контура.
• Работа но перемещению контура с током в магнитном поле
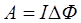 ,
,
где 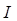 – сила тока в контуре;
– сила тока в контуре; 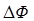 – изменение магнитного потока через поверхность, ограниченную замкнутым контуром (в случае перемещения проводника в магнитном поле
– изменение магнитного потока через поверхность, ограниченную замкнутым контуром (в случае перемещения проводника в магнитном поле 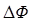 – поток, «заметаемый» проводником при перемещении).
– поток, «заметаемый» проводником при перемещении).
Методические указания и примеры решения задач
При решении задач по данной теме необходимо:
· показать на рисунке направление сил, действующих со стороны магнитного поля на проводник с током или движущийся заряд;
· помнить, что сила, действующая со стороны магнитного поля на проводник с током или движущийся заряд, всегда перпендикулярна направлению вектора магнитной индукции;
· для определения направления силы применять правило левой руки: если левую руку расположить так, чтобы перпендикулярная проводнику составляющая вектора магнитной индукции входила в ладонь, а четыре вытянутых пальца указывали на направление движения положительных зарядов (по току), то отогнутый на 90° большой палец покажет направление силы;
· при наличии нескольких полей или сил различной природы использовать принцип суперпозиции;учитывать различное направление сил со стороны электрического и магнитного полей, действующих на движущийся заряд;
§ в случае равновесия системы проводников с током или зарядов использовать для каждого из них общие условия равновесия: 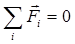 ,
, 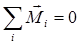 .
.
Пример 2.8. В однородном магнитном поле (В = 0,02 Тл) в плоскости, перпендикулярной линиям индукции, расположено проволочное полукольцо длиной 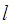 = 3 см, по которому течет ток
= 3 см, по которому течет ток 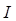 = 0,1 А. Найти силу, действующую на полукольцо, если подводящие провода находятся вне поля.
= 0,1 А. Найти силу, действующую на полукольцо, если подводящие провода находятся вне поля.
Дано: В = 0,02 Тл, l= 3 см, I = 0,1 A; F- ?
Решение
Согласно закону Ампера сила 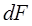 , действующая на элемент тока
, действующая на элемент тока 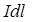 со стороны магнитного поля В, определяется по формуле
со стороны магнитного поля В, определяется по формуле 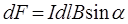 , где
, где 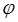 – угол между направлением поля
– угол между направлением поля 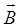 и тока
и тока 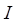 , равный по условию задачи 90°. Поэтому
, равный по условию задачи 90°. Поэтому 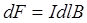 . Направление силы
. Направление силы 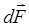 , определяемое по правилу левой руки, показано на рис.2.
, определяемое по правилу левой руки, показано на рис.2.
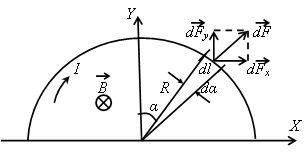
Рис.2.
При переходе от одного элемента полукольца к другому направление элементарных сил, оставаясь радиальным, непрерывно меняется. Поэтому искомую результирующую силу F будем искать по формуле 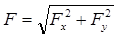 , где
, где 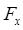 и
и 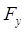 - проекции силы F на координатные оси X и Y. Эти проекции определяются интегрированием:
- проекции силы F на координатные оси X и Y. Эти проекции определяются интегрированием:
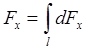 ,
, 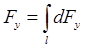 ,
,
где dFx и dFy – проекции элементарных сил dF на координатные оси, символ 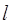 указывает на то, что интеграл берется по всей длине полукольца. Учитывая симметрию полукольца, имеем
указывает на то, что интеграл берется по всей длине полукольца. Учитывая симметрию полукольца, имеем 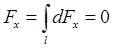 . Тогда результирующая сила
. Тогда результирующая сила
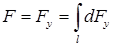 . (1)
. (1)
Из рис.2 следует 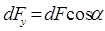 , или, после подстановки
, или, после подстановки 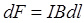 ,
, 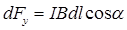 . Поскольку
. Поскольку 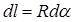 , где
, где 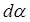 – угол, стягиваемый дугой dl, то
– угол, стягиваемый дугой dl, то 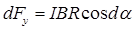 . Теперь введем dFy под знак интеграла (1) и проинтегрируем по
. Теперь введем dFy под знак интеграла (1) и проинтегрируем по 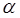 в пределах от
в пределах от 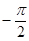 до
до 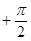 :
:
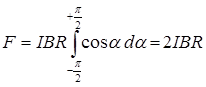 .
.
Подставив в правую часть полученного равенства 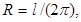 получим окончательно
получим окончательно
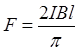 . (2)
. (2)
Проверим, дает ли правая часть (2) единицу силы (Н):
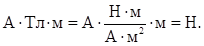
Подставив значения величин в (2), найдем 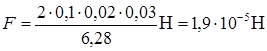 .
.
Согласно выражению (1) сила F направлена вдоль оси Х. Заметим, что если полукольцо распрямить, то все элементарные силы 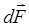 будут направлены вдоль оси Y, что приведет к увеличению результирующей силы; если же полукольцо превратить в кольцо, то последнее будет растягиваться или сжиматься в зависимости от направления тока в кольце.
будут направлены вдоль оси Y, что приведет к увеличению результирующей силы; если же полукольцо превратить в кольцо, то последнее будет растягиваться или сжиматься в зависимости от направления тока в кольце.
Пример 2.9. Рядом с бесконечно длинным проводом, по которому течет ток силы 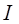 = 5 А, расположена квадратная рамка со стороной
= 5 А, расположена квадратная рамка со стороной 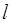 = 10 см и током
= 10 см и током 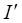 = 0,2 А. Рамка лежит в одной плоскости с проводником, так, что ее сторона, ближайшая к проводу находится от него на расстоянии а = 5 см, ток в ней противоположен по направлению току
= 0,2 А. Рамка лежит в одной плоскости с проводником, так, что ее сторона, ближайшая к проводу находится от него на расстоянии а = 5 см, ток в ней противоположен по направлению току 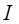 в проводе (см. рис.). Определить работу при удалении рамки из магнитного поля. Считать, что при движении рамки токи
в проводе (см. рис.). Определить работу при удалении рамки из магнитного поля. Считать, что при движении рамки токи 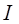 и
и 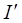 поддерживаются постоянными.
поддерживаются постоянными.
Дано: 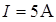 ,
, 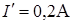 ,
, 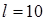 см,
см, 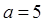 см ;
см ; 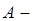 ?
?
Решение
Рассмотрим два способа решения задачи.
Первый способ Квадратная рамка с током 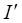 находится в неоднородном магнитном поле прямого проводника с током
находится в неоднородном магнитном поле прямого проводника с током 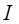 . Индукция этого поля
. Индукция этого поля
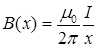 (1)
(1)
где x – расстояние от проводника до рассматриваемой точки поля.
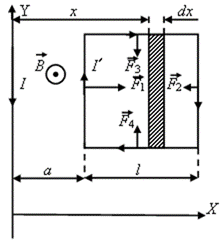
Сила, с которой поле действует на каждую сторону рамки, может быть определена суммированием элементарных сил Ампера
dF = I′ dlBsinα, (2)
где 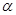 – угол между направлениями тока и поля.
– угол между направлениями тока и поля.
Направление сил, действующих на стороны рамки, определим по правилу левой руки. Учитывая, что для всех элементов одной и той же стороны рамки (левой или правой) величина индукции одинакова и sinα = 1, найдем силы, действующие на каждую из этих сторон:
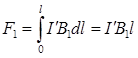 ,
, 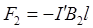 . (3)
. (3)
Что касается других сторон рамки (верхней и нижней), то поскольку они расположены одинаково по отношению к длинному проводу и токи в них противоположны по направлению, то действующие на них силы F 3 и F 4 должны быть уравновешенными. Следовательно, равнодействующая всех сил, приложенных к рамке, равна 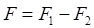 и направлена так, что рамка будет выталкиваться из поля. Используя выражения (1) и (3), представим силы
и направлена так, что рамка будет выталкиваться из поля. Используя выражения (1) и (3), представим силы 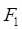 и
и 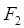 в следующем виде
в следующем виде
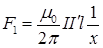
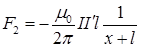 (4)
(4)
Работа выталкивания рамки из магнитного поля складывается из положительной работы силы 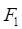 и отрицательной работы силы
и отрицательной работы силы 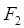 :
:
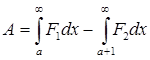 (5)
(5)
При вычислении работы А учтем, что сила 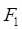 , переместив левую сторону рамки на расстояние
, переместив левую сторону рамки на расстояние 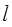 , при дальнейшем перемещении совершает такую же работу, как и сила
, при дальнейшем перемещении совершает такую же работу, как и сила 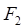 на всем пути перемещения правой стороны рамки, но с противоположным знаком. Таким образом,
на всем пути перемещения правой стороны рамки, но с противоположным знаком. Таким образом,
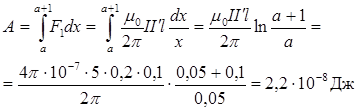
Второй способ. Для определения работ А можно воспользоваться формулой
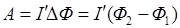 , (6)
, (6)
где 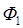 и
и 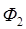 – магнитные потоки через площадь, ограниченную контуром, до и после ее перемещения. Поскольку вне поля магнитный поток через рамку Ф2 = = 0, то (6) принимает следующий вид:
– магнитные потоки через площадь, ограниченную контуром, до и после ее перемещения. Поскольку вне поля магнитный поток через рамку Ф2 = = 0, то (6) принимает следующий вид:
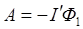 (7)
(7)
Поток 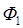 найдем по формуле:
найдем по формуле:
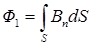 ,
,
где 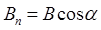 – проекция вектора
– проекция вектора 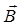 на нормаль к плоскости рамки. Поскольку вектор
на нормаль к плоскости рамки. Поскольку вектор 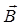 магнитного поля длинного провода перпендикулярен плоскости рамки и составляет угол
магнитного поля длинного провода перпендикулярен плоскости рамки и составляет угол 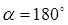 с ее нормалью, то
с ее нормалью, то 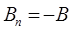 . Следовательно, поток
. Следовательно, поток 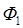 является отрицательным, а изменение потока
является отрицательным, а изменение потока 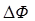 и работа, выражаемая формулой (6) – положительны. При вычислении
и работа, выражаемая формулой (6) – положительны. При вычислении 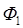 следует иметь в виду, что поле, в котором расположена рамка, неоднородно, т.е. зависит от
следует иметь в виду, что поле, в котором расположена рамка, неоднородно, т.е. зависит от 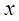 :
: 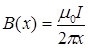 . Следовательно, элементарный поток
. Следовательно, элементарный поток 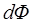 также будет зависеть от x:
также будет зависеть от x: 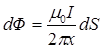 , где
, где 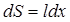 – площадь элементарной полоски длиной
– площадь элементарной полоски длиной 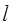 и шириной
и шириной 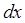 (полоска расположена параллельно длинному проводу). Тогда полный поток
(полоска расположена параллельно длинному проводу). Тогда полный поток
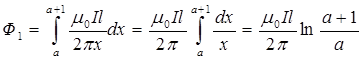
Подставив полученное выражение Ф в формулу (7), найдем
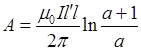
Этот результат совпадает с ответом, полученным первым способом.
Заметим, что в рассмотренном случае работа совершается за счет сил Ампера, действующих в плоскости рамки и выталкивающих рамку из магнитного поля, создаваемого длинным проводом с током. В действительности рамка находится в неустойчивом равновесии и при малейшем его нарушении может развернуться на 180°, после чего начнет притягиваться к длинному проводу. Однако в этом случае рамка будет двигаться так, что магнитный поток через нее будет увеличиваться 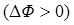 . Можно убедиться, что формула (6) справедлива для расчета работы по перемещению контура любой формы, в произвольном по конфигурации магнитном поле и произвольном перемещении. В случае проводника конечных размеров формула (6) тоже считается справедливой, усложняется лишь расчет величины
. Можно убедиться, что формула (6) справедлива для расчета работы по перемещению контура любой формы, в произвольном по конфигурации магнитном поле и произвольном перемещении. В случае проводника конечных размеров формула (6) тоже считается справедливой, усложняется лишь расчет величины 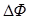 .
.
Дата: 2019-07-30, просмотров: 299.