Основные понятия и формулы
Явление электромагнитной индукции заключается в том, что при любом изменении магнитного потока 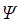 , сцепленного с данным контуром, в последнем возникает электродвижущая сила индукции
, сцепленного с данным контуром, в последнем возникает электродвижущая сила индукции 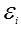 . Явление электромагнитной индукции описывается законом Фарадея и правилом Ленца.
. Явление электромагнитной индукции описывается законом Фарадея и правилом Ленца.
• Закон Фарадея. Величина ЭДС индукции пропорциональна скорости изменения магнитного потока:
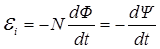 ,
,
где 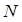 – число витков контура; Ф – поток через один виток;
– число витков контура; Ф – поток через один виток; 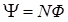 – потокосцепление; знак минус связан с правилом Ленца, определяющим направление тока индукции.
– потокосцепление; знак минус связан с правилом Ленца, определяющим направление тока индукции.
• Правило Ленца. ЭДС индукции, а, следовательно, и индукционный ток в контуре всегда имеют такое направление, что магнитное поле индуцированного тока препятствует тем изменениям основного потока магнитного поля, которые вызвали появление индукционного тока.
• Потокосцепление контура
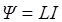 , где
, где 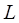 – индуктивность;
– индуктивность; 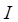 – сила тока в контуре.
– сила тока в контуре.
• Индуктивность соленоида с немагнитным сердечником 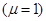
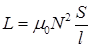 ,
,
где 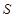 ,
, 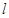 - соответственно, площадь поперечного сечения и длина соленоида.
- соответственно, площадь поперечного сечения и длина соленоида.
Ток индукции в контуре с сопротивлением R
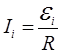 .
.
• Полный заряд, протекающий по контуру за время 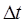 изменения магнитного потока,
изменения магнитного потока,
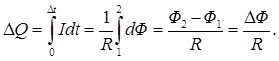 .
.
• ЭДС индукции на концах проводника, движущеюся с постоянной скоростью 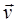 в магнитном поле с индукцией
в магнитном поле с индукцией 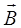 ,
,
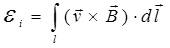 ,
,
где 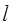 – длина проводника.
– длина проводника.
• Энергия магнитного поля, связанного с контуром индуктивностью L, по которому течет ток 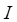 ,
,
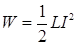 .
.
Методические указания и примеры решения задач
При решении задач на данную тему необходимо:
§ применять закон Фарадея при любом изменении магнитного потока через поверхность, ограниченную проводящим контуром, или перемещении проводника в магнитном поле;
§ учитывать, что величина ЭДС индукции определяется скоростью изменения магнитного потока и не зависит от величины потока;
§ иметь в виду, что закон сохранения энергии выполняется для любых физических процессов и явлений: не составляет исключение и явление электромагнитной индукции: получение тока индукции всегда связано с работой, которую необходимо совершить, чтобы тем или иным способом изменить потокосцепление.
Анализ задачи следует начинать с определения причин, вызвавших изменение магнитного потока или причин перераспределения зарядов. Это позволяет найти по правилу Ленца знак ЭДС индукции и направление тока индукции. Если дан замкнутый контур, поток через который изменяется по тем или иным причинам, то его следует выразить как функцию времени. Тогда ЭДС индукции может быть найдена путем последующего дифференцирования этой функции. Если дан проводник и в задаче требуется найти разность потенциалов на концах проводника, движущегося в магнитном ноле, то надо иметь в виду, что искомая разность потенциалов численно равна ЭДС индукции в проводнике. В этом случае, в зависимости от условия задачи, ЭДС индукции находят либо тоже по формуле, выражающей закон Фарадея, где под 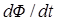 следует понимать магнитный поток, пересекаемый движущимся проводником в единицу времени, либо исследуя силы Лоренца, действующие на свободные заряды в движущемся проводнике.
следует понимать магнитный поток, пересекаемый движущимся проводником в единицу времени, либо исследуя силы Лоренца, действующие на свободные заряды в движущемся проводнике.
Пример 2.10. Рамка площадью 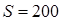 см
см 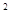 равномерно вращается с частотой
равномерно вращается с частотой 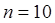 с
с 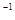 относительно оси, лежащей в плоскости рамки. Ось вращения перпендикулярна линиям индукции однородного магнитного поля
относительно оси, лежащей в плоскости рамки. Ось вращения перпендикулярна линиям индукции однородного магнитного поля 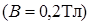 . Каково максимальное и среднее значения ЭДС индукции за время, в течение которого магнитный поток, пронизывающий рамку, изменится от максимального значения до нуля?
. Каково максимальное и среднее значения ЭДС индукции за время, в течение которого магнитный поток, пронизывающий рамку, изменится от максимального значения до нуля?
Дано: 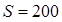 см
см 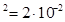 м
м 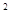 ,
, 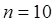 с
с 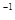 ,
, 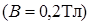 ;
; 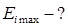
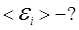
Решение
На рисунке показано мгновенное положение рамки под углом φ к направлению магнитного поля. Угол между нор-малью к рамке и направлением магнитного поля, как видно из рисунка, 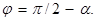 Поэтому поток, пронизывающий рам-ку,
Поэтому поток, пронизывающий рам-ку, 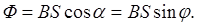 Учитывая, что за время
Учитывая, что за время 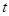 угол поворота
угол поворота 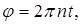 где n – частота вращения рамки (число оборотов, совершаемых рамкой за 1 с), для изменения потока со временем можно записать
где n – частота вращения рамки (число оборотов, совершаемых рамкой за 1 с), для изменения потока со временем можно записать
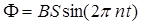 . (1)
. (1)
Согласно закону Фарадея ЭДС индукции определяется скоростью изменения потока:
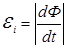 . (2)
. (2)
Подставив в формулу (2) выражение (1) и продифференцировав по времени, найдем зависимость мгновенного значения ЭДС индукции от времени:
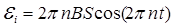 . (3)
. (3)
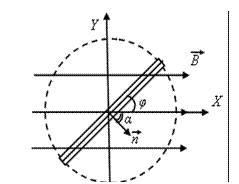 Максимальное значение ЭДС (амплитуда):
Максимальное значение ЭДС (амплитуда):
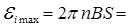
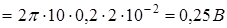
Для нахождения среднего значения ЭДС индукции следует воспользоваться формулой
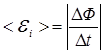
где 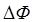 – изменение магнитного потока за время
– изменение магнитного потока за время 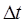 поворота рамки из положения, при котором рамка параллельна магнитному полю в положение, при котором она перпендикулярна ему. За это время рамка повернется на угол
поворота рамки из положения, при котором рамка параллельна магнитному полю в положение, при котором она перпендикулярна ему. За это время рамка повернется на угол 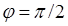 . Поток при этом изменится от значения Ф1 = 0 до значения Ф2 = BS. Изменение потока за это время составит ΔФ = BS. Время Δt найдем из условия
. Поток при этом изменится от значения Ф1 = 0 до значения Ф2 = BS. Изменение потока за это время составит ΔФ = BS. Время Δt найдем из условия 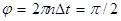 . Отсюда получаем
. Отсюда получаем 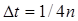 . Следовательно, искомое среднее значение ЭДС индукции
. Следовательно, искомое среднее значение ЭДС индукции
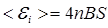 . (4)
. (4)
Убедимся в том, что правая часть полученной расчетной формулы дает единицу ЭДС вольт (В):
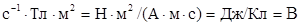 .
.
Производя вычисления по формуле (4), получим
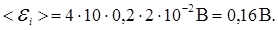
Задачи данного параграфа связаны с расчетом магнитного поля при наличии магнитных сред и базируются на знании свойств диа-, пара- и ферромагнетиков. Расчет полей значительно упрощается введением вектора напряженности 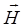 , как характеристики магнитного поля, определяемой через векторы
, как характеристики магнитного поля, определяемой через векторы 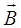 и
и 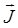 соотношением
соотношением 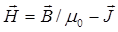 . Особенность вектора
. Особенность вектора 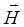 состоит в том, что его циркуляция не зависит от магнитных свойств среды, в которой находится выбранный контур интегрирования, а определяется лишь алгебраической суммой токов проводимости, охватываемых этим контуром. Вектор
состоит в том, что его циркуляция не зависит от магнитных свойств среды, в которой находится выбранный контур интегрирования, а определяется лишь алгебраической суммой токов проводимости, охватываемых этим контуром. Вектор 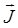 – магнитный момент, возникающий при намагничивании среды. Вектор
– магнитный момент, возникающий при намагничивании среды. Вектор 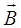 характеризует магнитное поле с учетом влияния среды.
характеризует магнитное поле с учетом влияния среды.
При решении уравнения, полученного в результате применения теоремы о циркуляции вектора 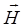 , часто используется соотношение
, часто используется соотношение 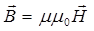 . При этом важно обращать внимание на то, что относительная магнитная проницаемость
. При этом важно обращать внимание на то, что относительная магнитная проницаемость 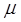 ферромагнетика сама зависит от
ферромагнетика сама зависит от 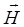 и является величиной переменной.
и является величиной переменной.
Важно также, что магнитные свойства сердечника зависят от его формы. В рассматриваемых ниже решениях задач это показано на примере сердечников, имеющих форму тора сплошного или с узким воздушным зазором.
Интерференция света
Основные понятия и формулы
Интерференция света — усиление или ослабление света в результате сложения двух (или нескольких) световых волн с одинаковыми частотами и с независящей от времени разностью фаз (такие волны называют когерентными).
· Оптическая разность хода D двух лучей, один из которых проходит путь длиной l1 в среде с показателем преломления n1, а с другой - путь l2 в среде с показателем преломления n2
D = l2n2 – l1n1.
· Условие максимального усиления света (интерференционные максимумы)
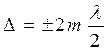 ,
,
где m = 0,1,2,...; l – длина волны.
· Условие максимального ослабления света (интерференционные минимумы)
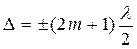 ,
,
где m = 0,1,2,..; l – длина волны.
· Оптическая разность хода лучей в тонких пленках в отраженном свете
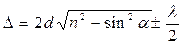 ,
,
где d – толщина пленки; n – показатель преломления вещества пленки; a – угол падения. 
· Радиусы темных колец Ньютона в отраженном свете
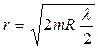 ,
,
где m = 1,2,3,... – порядковый номер кольца, R – радиус кривизны линзы.
· Радиусы светлых колец Ньютона в отраженном свете
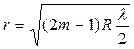 ,
,
где m = 1,2,3,... – порядковый номер кольца, R – радиус кривизны линзы.
Методические указания и примеры решения задач
В качестве общего подхода к решению задач на интерференцию света используются следующие действия:
1) выясняются причины появления оптической разности хода между интерферирующими лучами и находится эта разность;
2) записываются условия интерференционных максимумов или минимумов;
3) из этих условий и определяется искомая величина.
Задачи на интерференцию света в основном делятся на две группы.
К задачам первой группы относятся случаи интерференции, полученной с помощью зеркала Ллойда, зеркал Френеля, бипризмы Френеля, в опыте Юнга др. В этих задачах для расчета интерференционной картины удобно данную оптическую систему заменить другой, эквивалентной, считая при этом, что имеется не один, а два когерентных источника.
Вторую группу составляют задачи на интерференцию в плоскопараллельных, клинообразных тонких слоях, а также задачи на кольца Ньютона.
При решении этих задач следует обратить внимание на то, что разность фаз когерентных волн при встрече, и, следовательно, результат интерференции, обусловлены двумя причинами: оптической разностью хода и условиями отражения обеих волн.
Если отражение происходит от границы с оптически более плотной средой, фаза волны претерпевает изменение на π. Если отражение происходит от границы с оптически менее плотной средой, то скачка фазы не происходит.
Пример 2.11 На толстую стеклянную пластинку с показателем преломления 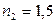 , покрытую тонким слоем пленки с показателем преломления
, покрытую тонким слоем пленки с показателем преломления 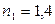 , под углом
, под углом 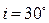 падает пучок лучей монохроматического света с длиной волны
падает пучок лучей монохроматического света с длиной волны 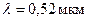 . Определить минимальную толщину пленки, если отраженный свет максимально ослаблен.
. Определить минимальную толщину пленки, если отраженный свет максимально ослаблен.
Дано: 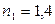 ,
, 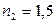 ,
, 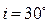 ,
, 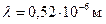 ;
; 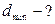
Решение
На границу раздела воздух-пленка падает плоская монохроматическая волна, угол падения которой 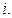 На границе раздела волна частично отражается, частично преломляется. Волны, отраженные от верхней поверхности пластинки и отраженные от нижней и затем преломленные на верхней, будут когерентными и при наложении интерферируют.
На границе раздела волна частично отражается, частично преломляется. Волны, отраженные от верхней поверхности пластинки и отраженные от нижней и затем преломленные на верхней, будут когерентными и при наложении интерферируют.
Результат интерференции зависит от того, какому условию удовлетворяет оптическая разность хода.
Отраженный свет максимально ослаблен, следовательно, при интерференции выполняется условие минимума:
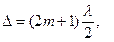 где
где 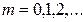
Оптическая разность хода указанных волн
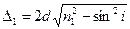 .
.
Волна, отраженная от верхней поверхности пленки, изменяет фазу на π и точно также на π изменится фаза волны, отраженной от нижней поверхности пленки. Поэтому добавочная разность фаз и разность хода не возникает 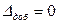 .
.
Таким образом, оптическая разность хода указанных волн
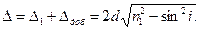
Условие минимума освещенности:
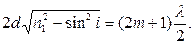
Найдем толщину пленки d:
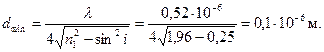
Пример 2.12 При освещении клина с углом 2,2·10–4 рад пучком параллельных лучей с длиной волны 0,66 мкм, падающим нормально к поверхности, образуются интерференционные полосы, причем на длине 1 см, укладываются 10 темных полос. Определить показатель преломления материала пластины.
Дано: α = 2,2·10–4 рад, λ = 0,66 мкм, l = 10–2 м, Ν = 10; n = ?
Решение
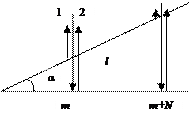 В данном случае интерферируют лучи 1 и 2 отраженные от двух поверхностей клина (рис. ). Так как интерференция на клине наблюдается при малых углах α, лучи 1 и 2 можно считать параллельными.
В данном случае интерферируют лучи 1 и 2 отраженные от двух поверхностей клина (рис. ). Так как интерференция на клине наблюдается при малых углах α, лучи 1 и 2 можно считать параллельными.
Оптическую разность хода лучей можно определить по формуле 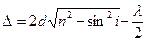 , учтя, что при нормальном падении лучей на пластину i = 0. Условие m-го интерференционного минимума может быть записано в виде
, учтя, что при нормальном падении лучей на пластину i = 0. Условие m-го интерференционного минимума может быть записано в виде
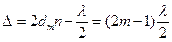 , или
, или 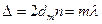 ,
,
где 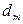 – толщина клина в том месте, где наблюдается темная полоса, соответствующая номеру m.
– толщина клина в том месте, где наблюдается темная полоса, соответствующая номеру m.
Пусть темной полосе m + N соответствует толщина 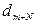 . Тогда
. Тогда 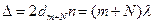 . Согласно условию задачи на расстоянии l укладывается Ν полос. Из рисунка видно, что
. Согласно условию задачи на расстоянии l укладывается Ν полос. Из рисунка видно, что 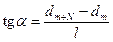 . Учитывая, что при малых углах
. Учитывая, что при малых углах 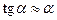 и подставляя значения
и подставляя значения 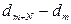 , получим
, получим 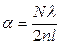 .
.
Отсюда находим показатель преломления
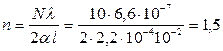 .
.
Дифракция света
Основные понятия и формулы
Дифракция света — явления, связанные с отклонением светового луча от прямолинейности при распространении света в среде с резкими неоднородностями.
· Радиусы зон Френеля для сферического волнового фронта
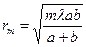 , (1)
, (1)
где m = 1,2,3,... – порядковый номер зоны; l – длина волны света; a – расстояние от источника света до сферического фронта волны; b – расстояние от сферического фронта волны до точки наблюдения.
Дата: 2019-07-30, просмотров: 306.