Основные понятия и формулы

· Электрическая емкость уединенного проводника 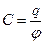, где q- заряд, сообщенный проводнику; φ – потенциал проводника, иначе: C – коэффициент пропорциональности между зарядом и потенциалом на поверхности провуодника.

· Электроемкость конденсатора 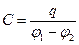 , где - разность потенциалов на обкладках конденсакора.

· Электрическая емкость уединенной проводящей сферы радиусом R, находящейся в бесконечной среде с диэлектрической проницаемостью ε, .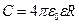

· Электрическая емкость плоского конденсатора 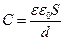, где S- площадь каждой пластины, d-расстояние между ними, ε- диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами.

· Электрическая емкость последовательно соединенных 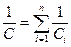конденсаторов , где n- число конденсаторов.

· Электрическая емкость параллельно соединенных конденсаторов .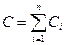

· Энергия заряженного проводника .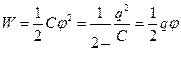

· Энергия заряженного конденсатора 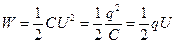, где C- емкость конденсатора; q – заряд обкладок, U-разность потенциалов между ними.

· Объемная плотность энергии электрического поля 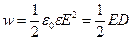, где E- напряженность электрического поля, D – электрическое смещение.

Пример 2.4. Плоский воздушный конденсатор с площадью пластин 500 см  подключен к источнику тока, ЭДС которого 200 В. Определить работу внешних сил по раздвижению пластин, если пластины в процессе раздвижения: 1) отключены от источника тока; 2) остаются подключенными к источнику тока.

Дано: S=500 см , d  =1см, d 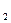= 2см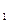, ( d и d 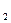- начальное и конечное расстояние между пластинами), E=200В; А- ?

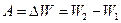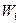Решение: В первом случае, когда конденсатор отключен от источника тока, систему пластин можно рассматривать как изолированную и для нее справедлив закон сохранения энергии. Тогда работа внешних сил определится как изменение энергии системы: , где  и 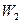- энергия поля конденсатора в начальном и конечном состояниях . Поскольку при раздвижении пластин отключенного конденсатора заряд на них не изменяется, то энергию удобно выразить через заряд, т.е .

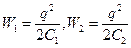В результате получим: 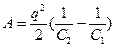, если учесть, что емкость плоского конденсатора определяется как 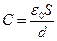, а заряд и напряжение на пластинах конденсатора связаны: 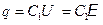. Найдем

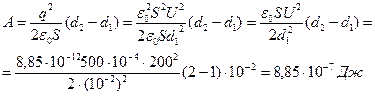
Во втором случае конденсатор не является изолированной системой: напряжение U на пластинах конденсатора остается неизменным , а напряженность поля , заряд на пластинах и емкость будут изменятся при изменении d ,т.к. 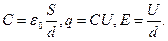 Поэтому элементарная работа по перемещению заряда q пластины в поле E₂, другой пластины будет непрерывно меняться с изменением расстояния x между пластинами (d₁≤ x≤ d₂). Элементарная работа силы E₂∙q на пути dx: 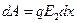. Здесь  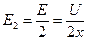- напряженность поля одной пластины, а 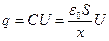. Таким образом, 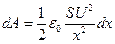, а работа по раздвижению пластин конденсатора в пределах от d₁ до d₂ будет:

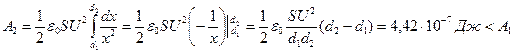, т. к. .

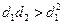Закон Ома.

Основные понятия и формулы

· Сила тока 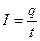, или 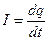, где  q- количество электричества, прошедшее через поперечное сечение проводника за время t

· Плотность тока 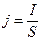   или 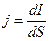 , где  S – площадь поперечного сечения проводника

· Сопротивление однородного проводника 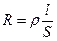, где ρ – удельное сопротивление проводника, l- его длина

· Проводимость G проводника и удельная проводимость 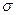 вещества :

·                                   

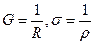
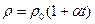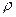Зависимость удельного сопротивления от температуры , где  и 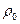- удельные сопротивления, соответственно при t и 0 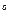С, 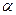 - температурный коэффициент сопротивления