Контрольная работа №2
Электростатика и постоянный ток
Электростатическое поле
Основные понятия и формулы
Электростатика изучает электрическое поле неподвижных зарядов (дискретных и однородно распределенных)
- Закон Кулона
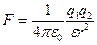 ,
,
где F – сила взаимодействия двух точечных зарядов q1 и q2 на расстоянии r; ε – диэлектрическая проницаемость среды (безразмерная величина, ε = 1 в вакууме); ε0 = 8,85·10-12Ф/м – электрическая постоянная. Фарада – единица электроемкости.
· Закон сохранения заряда 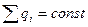 означает, что алгебраическая
означает, что алгебраическая
сумма электрических зарядов изолированной системы сохраняется.
· Напряженность электрического поля 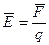 - это сила, действующая со стороны пволя на единичный точечный заряд, помещенный в данную точку поля.
- это сила, действующая со стороны пволя на единичный точечный заряд, помещенный в данную точку поля.
· Напряженность поля точечного заряда в вакууме 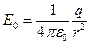 .
.
В диэлектрике 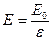 , где
, где 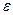 - диэлектрическая проницаемость диэлектрика, а
- диэлектрическая проницаемость диэлектрика, а 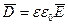 - вектор электрического смещения.
- вектор электрического смещения.
· Циркуляция вектора E по замкнутому контуру L: 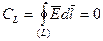 .
.
· Работа электростатической силы по замкнутому контуру 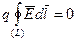 .
.
· Поток вектора E через замкнутую поверхность 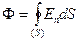 , где En – проекция
, где En – проекция 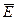 на нормаль
на нормаль 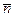 к элементу поверхности dS
к элементу поверхности dS
· Теорема Остроградского-Гаусса 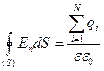 , где
, где 
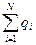 - алгебраическая сумма зарядов внутри замкнутой поверхности S.
- алгебраическая сумма зарядов внутри замкнутой поверхности S.
· Принцип суперпозиции электрических полей
Напряженность поля двух и более точечных зарядов в данной точке пространства равна геометрической сумме напряженностей, создаваемых этими зарядами, т.е. 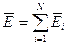
· Напряженность поля бесконечно длинной равномерно заряженной нити на расстоянии r от ее оси, 

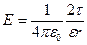 , где τ – линейная плотность заряда т.е. заряд единицы длины [Кл / м] .
, где τ – линейная плотность заряда т.е. заряд единицы длины [Кл / м] .
· Напряженность поля металлической сферы радиусом R, несущей заряд Q, на расстоянии r от центра сферы:
E = 0 (при r < R);
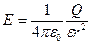 (при r>R);
(при r>R);
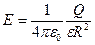 (при r = R).
(при r = R).
· Напряженность поля бесконечной равномерно заряженной плоскости
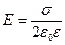 , где σ – поверхностная плотность заряда, т.е. заряд единицы площади [Кл/м2].
, где σ – поверхностная плотность заряда, т.е. заряд единицы площади [Кл/м2].
Методические указания и примеры решения задач
Метод расчета электростатического поля выбирается в зависимости от того, как распределены заряды в пространстве.
- Электрическое поле системы точечных зарядов вычисляется методом суперпозиции полей:
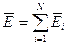 .
.
2. Поля однородного распределения зарядов на телах симметричной формы (плоскостях, нитях, сферах, шарах, цилиндрах и т. д.) вычисляются методом Гаусса. Реализация метода начинается с записи теоремы Гаусса 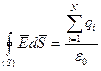 ,затем выбирается поверхность, согласованная с симметрией заряженного тела, т.е. поверхность S должна быть геометрическим местом точек, для которых E=const . Тогда поток
,затем выбирается поверхность, согласованная с симметрией заряженного тела, т.е. поверхность S должна быть геометрическим местом точек, для которых E=const . Тогда поток 
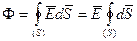 . Далее подсчитав заряды внутри этой поверхности по теореме Гаусса определяют E.
. Далее подсчитав заряды внутри этой поверхности по теореме Гаусса определяют E.
3. Поля однородного распределения зарядов любой симметрии вычисляют методом дифференцирования-интегрирования (ДИ), при этом используется принцип суперпозиции электрических полей, созданных квазиточечными зарядами. Реализация метода ДИ осуществляется в три этапа:
a) Анализ задачи и запись нужного физического закона (например, закона Кулона, или формулы для E ) в дифференциальной форме. Это расширяет область использования закона (формулы), позволяя применить его (их) к неточечным зарядам.
b) Подготовка дифференциальной формы (пункт а)) к интегрированию: выбор удобной переменной интегрирования, учет симметрии задачи и т.п.
c) Интегрирование рабочей формулы 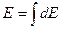 ,
, 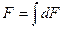 и т. д.
и т. д.
Пример 2.1.
Использовать метод Гаусса для нахождения напряженности 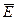 поля равномерно заряженной нити с линейной плотностью τ (Кл/м).
поля равномерно заряженной нити с линейной плотностью τ (Кл/м).
Дано: τ ; Eнити(r) - ?
Решение: Выбираем замкнутую поверхность Гаусса в виде цилиндра длиной l и радиусом r, соосного с нитью. В силу осевой (аксиальной) симметрии величина напряженности E будет одинаковой в любой точке боковой поверхности цилиндра. Поэтому поток напряженности через замкнутую цилиндрическую поверхность S будет 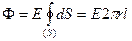 , так как поток
, так как поток 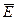 через основания цилиндра равен 0, а суммарный заряд внутри S равен τ l, то по теореме Гаусса
через основания цилиндра равен 0, а суммарный заряд внутри S равен τ l, то по теореме Гаусса 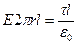 или
или 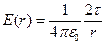 .
.
Анализ результата: полученное выражение показывает, что поле вокруг нити неоднородно 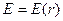 , в отличие, например, от поля однородно заряженной плоскости. /Уместно упомянуть о сходстве полученной формулы с выражением индукции магнитного поля прямого тока I:
, в отличие, например, от поля однородно заряженной плоскости. /Уместно упомянуть о сходстве полученной формулы с выражением индукции магнитного поля прямого тока I: 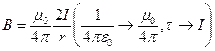 .
.
Пример 2.2.
Определить напряженность поля отрезка однородно заряженной нити в точке О, не лежащей против середины данного отрезка и находящейся на расстоянии r0 от него. Линейная плотность заряда нити τ, длина нити l.
Дано : l, τ , r0, Eo(ro) - ?
Решение: Равномерная заряженность отрезка нити и отсутствие высокой симметрии (центральной и аксиальной) в задаче заставляют обратиться к методу ДИ. Выделим на отрезке квазиточечный заряд dq = τ dl и определим поле dE0 этого заряда в точке 0. Искомая напряженность Eo( ro) получится в результате суперпозиции напряженностей dE0 от всех dl, составляющих отрезок l. Асимметричное расположение точки О относительно концов отрезка приводит к тому, что результирующий вектор Eo( ro) будет иметь составляющие Eox = Eo cosα и Eoy = Eo sinα ,которые определяют интегрированием dEox и dEoy соответственно. Отметим, что при интегрировании линейные переменные необходимо заменить на более удобные угловые т.е. ( r, dl→ α, dα ). Из рассмотрения подобных заштрихованных треугольников получим: 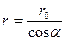 ,
,
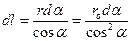 . В результате необходимые для интегрирования dEox и dEoy будут выглядеть следующим образом:
. В результате необходимые для интегрирования dEox и dEoy будут выглядеть следующим образом:
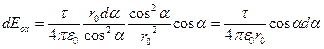 ,
, 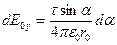 .
.
Третий этап метода ДИ- интегрирование:
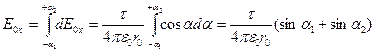
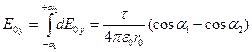
Анализ результата: При α1 =α2=α задача становится симметричной и E0 y =0, а
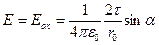 , что на множитель sinα отличается от напряженности поля бесконечной нити. Рассматриваемый отрезок превращается в такую нить при
, что на множитель sinα отличается от напряженности поля бесконечной нити. Рассматриваемый отрезок превращается в такую нить при 
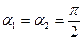 и в этом случае
и в этом случае 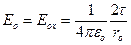 . Таким образом, наш результат позволяет получить известные формулы как частный случай. Это подтверждает его правильность.
. Таким образом, наш результат позволяет получить известные формулы как частный случай. Это подтверждает его правильность.
Потенциал. Работа по перемещению заряда в электростатическом поле.
Основные понятия и формулы.
· Потенциал электростатического поля 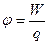 -это потенциальная энергия единичного положительного заряда, помещенного в данную точку поля.
-это потенциальная энергия единичного положительного заряда, помещенного в данную точку поля.
· 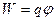 - Потенциальная энергия заряда q в поле с потенциалом φ.
- Потенциальная энергия заряда q в поле с потенциалом φ.
· 
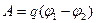 - работа по перемещению заряда q из точки поля с потенциалом φ1 в точку с потенциалом φ2 ; работа сил поля в этом случае может быть также рассчитана
- работа по перемещению заряда q из точки поля с потенциалом φ1 в точку с потенциалом φ2 ; работа сил поля в этом случае может быть также рассчитана 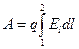 , где El – проекция вектора Е на направление перемещения dl .
, где El – проекция вектора Е на направление перемещения dl .
· Связь напряженности и потенциала электростатического поля
· 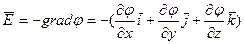 или
или 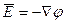 , где
, где 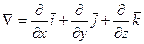 - векторный дифференциальный оператор (Набла ).
- векторный дифференциальный оператор (Набла ).
· Для однородного поля напряженностью E разность потенциалов 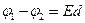 , где d – расстояние между точками с потенциалами φ1 и φ2 .
, где d – расстояние между точками с потенциалами φ1 и φ2 .
· Потенциал электрического поля, создаваемого точечным зарядом Q на расстоянии r от заряда 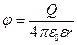 , где ε – диэлектрическая проницаемость среды, окружающей заряд
, где ε – диэлектрическая проницаемость среды, окружающей заряд
· Потенциал электрического поля, создаваемого сферической поверхностью с зарядом Q и радиуса R, в точке удаленной на расстояние r от центра сферы:
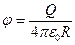 ( при
( при 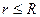 );
);
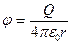 ( при
( при 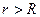 ) .
) .
Видно, что последняя формула совпадает с выражением для потенциала точечного заряда.
· Потенциал электрического поля, создаваемого системой n точечных зарядов согласно принципу суперпозиции электрических полей равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности: 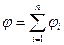 .
.
Методические указания и примеры решения задач
Метод расчета потенциалов электрических полей ,также как и напряженностей, определяется распределением зарядов в пространстве.
Потенциал системы точечных зарядов рассчитывается по принципу суперпозиции.
Потенциал поля непрерывно распределенных зарядов рассчитывается методом не сам потенциал, а разность потенциалов. Так, например, формула 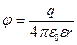 выражает потенциал поля точечного заряда на расстоянии r от него, справедлива в предположении, что потенциал φ=0 при r→∞.
выражает потенциал поля точечного заряда на расстоянии r от него, справедлива в предположении, что потенциал φ=0 при r→∞.
В основе метода определения разности потенциалов лежит соотношение
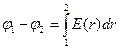 , связывающее разность потенциалов двух точек поля с напряженностью в области между этими точками. Задача такого рода упрощается в случае симметричных полей с заранее известным распределением напряженности E( r).
, связывающее разность потенциалов двух точек поля с напряженностью в области между этими точками. Задача такого рода упрощается в случае симметричных полей с заранее известным распределением напряженности E( r).
Пример2.3 Положительный заряд q равномерно распределен по кольцу радиуса R . Найти потенциал на оси кольца как функцию расстояния h от центра кольца.
Дано: q,R; 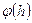 ?
?
Решение: Заряд, распределенный по кольцу , нельзя считать точечным поэтому воспользуемся методом ДИ. Разобьем кольцо на элементарные отрезки dl .Заряд такого отрезка будет 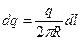 , а потенциал , создаваемый этим зарядом , можно определить по формуле потенциала точечного заряда ,тогда получим:
, а потенциал , создаваемый этим зарядом , можно определить по формуле потенциала точечного заряда ,тогда получим: 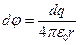 , где r- расстояние от элемента кольца до точки, в которой определяется потенциал,т.е
, где r- расстояние от элемента кольца до точки, в которой определяется потенциал,т.е 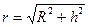
Подставив это выражение в 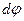 и интегрируя, найдем
и интегрируя, найдем 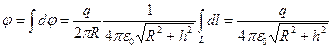 .
.
Анализ полученной функции φ( h) показывает:
- Потенциал поля в произвольной точке на оси кольца зависит от заряда q и не зависит от того является ли распределение заряда по кольцу равномерным или неравномерным;
- Потенциал является положительным для всех значений h и имеет максимальное значение в центре кольца.
Закон Ома.
Основные понятия и формулы
· Сила тока 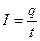 , или
, или 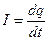 , где q- количество электричества, прошедшее через поперечное сечение проводника за время t
, где q- количество электричества, прошедшее через поперечное сечение проводника за время t
· Плотность тока 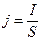 или
или 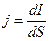 , где S – площадь поперечного сечения проводника
, где S – площадь поперечного сечения проводника
· Сопротивление однородного проводника 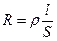 , где ρ – удельное сопротивление проводника, l- его длина
, где ρ – удельное сопротивление проводника, l- его длина
· Проводимость G проводника и удельная проводимость 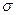 вещества :
вещества :
· 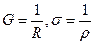
Зависимость удельного сопротивления от температуры 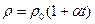 , где
, где 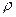 и
и 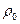 - удельные сопротивления, соответственно при t и 0
- удельные сопротивления, соответственно при t и 0 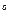 С,
С, 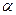 - температурный коэффициент сопротивления
- температурный коэффициент сопротивления
Правила Кирхгофа
Основные понятия и формулы
При расчете разветвленных электрических цепей постоянного тока пользуются двумя правилами (законами) Кирхгофа.
Первое правило относится к узлам цепей, т.е. к точкам, в которых сходятся не менее трех проводников: алгебраическая сумма сил токов, сходящихся в узле, равна нулю,т.е. 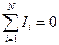 (при этом токи «втекающие» в узел считаются положительными, а «вытекающие» -отрицательными).
(при этом токи «втекающие» в узел считаются положительными, а «вытекающие» -отрицательными).
Второе правило относится к замкнутым контурам цепей: алгебраическая сумма напряжений на всех участках контура равна алгебраической сумме электродвижущих сил, действующих в нем, т.е 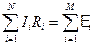 .При этом силы токов и ЭДС считаются положительными, если их направление совпадают с выбранным (произвольно) направлением обхода контура.
.При этом силы токов и ЭДС считаются положительными, если их направление совпадают с выбранным (произвольно) направлением обхода контура.
Пример 2.6. Определить все токи (I1…I5) в разветвленной цепи, если заданы R1…R5 и E1…E5.
Решение. Произвольно выбираем направление токов. Применяем 1-ое правило Кирхгофа к одному из двух узлов (только один независим): 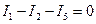 . Произвольно выбираем направление обхода в двух контурах (только два из трех контуров независимы). Применяем 2-ое правило Кирхгофа в выбранных контурах:
. Произвольно выбираем направление обхода в двух контурах (только два из трех контуров независимы). Применяем 2-ое правило Кирхгофа в выбранных контурах:
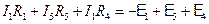
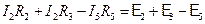
Таким образом, мы имеем три уравнения для трех неизвестных токов (I1, I2, I5). Получение отрицательного значения какого-либо тока означает, что первоначальный выбор направления этого тока был неправильным и его надо изменить.
Магнитостатика.
Расчет магнитных полей постоянных токов
различной конфигурации
Основные понятия и формулы
• Закон Био - Савара – Лапласа
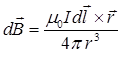 ,
,
где 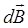 – вектор магнитной индукции, создаваемый элементом тока
– вектор магнитной индукции, создаваемый элементом тока 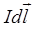 ;
; 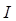 – сила тока;
– сила тока; 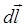 – вектор, равный по модулю длине элемента проводника и совпадающий по направлению с током;
– вектор, равный по модулю длине элемента проводника и совпадающий по направлению с током; 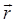 – радиус-вектор, проведенный от середины элемента
– радиус-вектор, проведенный от середины элемента 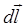 в точку, где определяется магнитная индукция;
в точку, где определяется магнитная индукция; 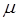 – магнитная проницаемость среды;
– магнитная проницаемость среды; 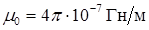 - магнитная постоянная .
- магнитная постоянная .
• Модуль вектора магнитной индукции
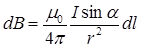 ,
,
где 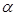 – угол между векторами
– угол между векторами 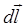 и
и 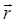 .
.
• Принцип суперпозиции магнитных полей

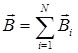 ,
,
где 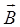 – магнитная индукция результирующего поля;
– магнитная индукция результирующего поля; 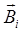 – магнитная индукция суммируемых полей:
– магнитная индукция суммируемых полей:
• Магнитная индукция в центре кругового проводника с током
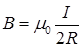 ,
,
где 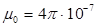 Гн/м – магнитная постоянная;
Гн/м – магнитная постоянная; 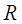 – радиус кривизны проводника;
– радиус кривизны проводника; 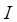 – сила тока.
– сила тока.
• Магнитная индукция поля в точке, лежащей на оси кругового проводника с током на расстоянии h от его центра,
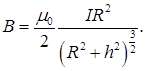
• Магнитная индукция поля, создаваемого участком проводника,
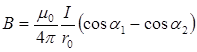 ,
,
где 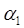 и
и 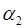 - углы между осью проводника и прямыми, проведенными из концов проводника в точку наблюдения (см. рис. 5).
- углы между осью проводника и прямыми, проведенными из концов проводника в точку наблюдения (см. рис. 5).
• Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током,
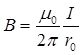 ,
,
где 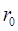 – расстояние от оси проводника до точки наблюдения.
– расстояние от оси проводника до точки наблюдения.
• Магнитная индукция поля, создаваемого соленоидом в средней его части (или тороидом на его оси),
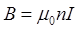 ,
,
где 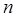 - число витков, приходящихся на единицу длины соленоида (тороида);
- число витков, приходящихся на единицу длины соленоида (тороида); 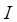 - сила тока в одном витке.
- сила тока в одном витке.
Методические указания и примеры решения задач
Математические методы расчета магнитных полей выбираются в зависимости от того, какова конфигурация токов, практически они являются теми же, что и методы расчета электрических полей.
При расчете магнитных полей необходимо:
- указать основные законы и формулы, на которых базируется решение задачи (если при решении задачи применяется формула, имеющая частный характер, не выражающая какой-либо физический закон или определение физической величины, её следует вывести);
- знать правила изображения магнитных полей: вектор
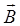 в каждой точке силовой линии направлен по касательной к ней, а густота линий пропорциональна значению
в каждой точке силовой линии направлен по касательной к ней, а густота линий пропорциональна значению 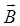 ; силовые линии магнитной индукции замкнуты, не пересекаются и не соприкасаются;
; силовые линии магнитной индукции замкнуты, не пересекаются и не соприкасаются; - применять для определения направления поля правило буравчика: если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитной индукции;
- знать, что мнемоническое правило буравчика связано с правилом векторного умножения векторов;
- использовать принцип суперпозиции парциальных (слагаемых) полей: магнитная индукция результирующего поля, создаваемого несколькими токами, равна векторной сумме магнитных индукций полей, создаваемых каждым током в отдельности.
Пример 2.7 Из проволоки длиной 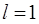 м сделана квадратная рамка. По рамке течет ток 1 = 10 А. Найти магнитную индукцию
м сделана квадратная рамка. По рамке течет ток 1 = 10 А. Найти магнитную индукцию 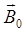 в центре рамки.
в центре рамки.
Дано: 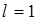 м, 1 = 10 А;
м, 1 = 10 А; 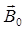 - ?
- ?
Решение
Согласно принципу суперпозиции полей магнитная индукция 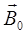 квадратной рамки равна векторной сумме магнитных индукций, создаваемых каждой стороной в отдельности:
квадратной рамки равна векторной сумме магнитных индукций, создаваемых каждой стороной в отдельности:
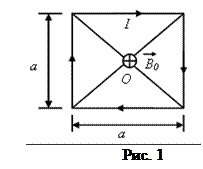
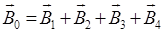 . Учитывая, что эти векторы и точке О имеют одинаковое направление и в силу симметрии рамки равны по модулю, имеем
. Учитывая, что эти векторы и точке О имеют одинаковое направление и в силу симметрии рамки равны по модулю, имеем 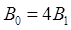 . Таким образом, задача нахождения
. Таким образом, задача нахождения 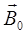 сводится к определению магнитной индукции, создаваемой одной из сторон рамки, например
сводится к определению магнитной индукции, создаваемой одной из сторон рамки, например 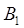 . Для определения
. Для определения 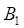 запишем сначала в дифференциальной форме основной закон, на котором основано решение задач:
запишем сначала в дифференциальной форме основной закон, на котором основано решение задач:
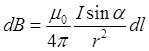
Принимая во внимание, что индукция магнитного поля каждого элемента тока 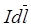 имеет в точке О одно и то же направление, получим
имеет в точке О одно и то же направление, получим
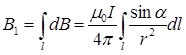
где символ l указывает, что интеграл берется по длине одной стороны рамки. Преобразуем подынтегральное выражение так, чтобы можно было проинтегрировать по углу 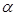 . Пусть элемент
. Пусть элемент 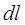 виден из точки О под углом
виден из точки О под углом 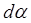 . Тогда длина дуги, стягивающей этот угол,
. Тогда длина дуги, стягивающей этот угол, 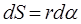 . С другой стороны, как это следует из малого прямоугольного треугольника ABC (см. рис.1), можно написать:
. С другой стороны, как это следует из малого прямоугольного треугольника ABC (см. рис.1), можно написать: 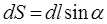 . Теперь, учитывая приведенное выражение
. Теперь, учитывая приведенное выражение 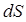 , найдем
, найдем 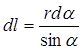 . Разделив левую и правую части найденного равенства на
. Разделив левую и правую части найденного равенства на 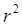 , получим
, получим 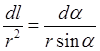 или
или 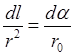 , где
, где 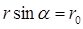 . Подставив это выражение под знак интеграла в формуле для магнитной индукции
. Подставив это выражение под знак интеграла в формуле для магнитной индукции 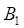 , получим
, получим
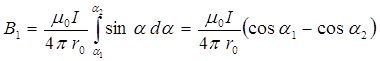 .
.
Учтем, что угол 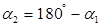 ; расстояние
; расстояние 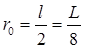 . Тогда магнитная индукция, создаваемая одной стороной рамки,
. Тогда магнитная индукция, создаваемая одной стороной рамки, 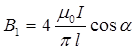 , а искомая магнитная индукция
, а искомая магнитная индукция 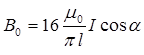 . Подставив значения величин, найдем
. Подставив значения величин, найдем
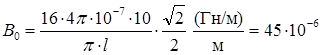 Тл
Тл 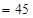 мкТл.
мкТл.
Направление вектора 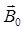 показано кружком с крестиком в центре рамки. Заметим, что при расчете магнитных полей постоянных токов, создаваемых проводниками произвольной конфигурации так же, как и при расчете электростатических полей, широко используется принцип суперпозиции. Закон Био – Савара – Лапласа сначала записывается в основной дифференциальной форме, затем подготавливается к интегрированию рабочая формула и осуществляется необходимое интегрирование.
показано кружком с крестиком в центре рамки. Заметим, что при расчете магнитных полей постоянных токов, создаваемых проводниками произвольной конфигурации так же, как и при расчете электростатических полей, широко используется принцип суперпозиции. Закон Био – Савара – Лапласа сначала записывается в основной дифференциальной форме, затем подготавливается к интегрированию рабочая формула и осуществляется необходимое интегрирование.
Основные понятия и формулы
• Закон Ампера
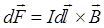 или
или 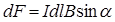 ,
,
где 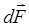 сила, действующая на элемент тока
сила, действующая на элемент тока 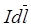 , помещенный в магнитное ноле с индукцией
, помещенный в магнитное ноле с индукцией 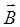 ;
; 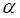 – угол между направлениями поля и тока.
– угол между направлениями поля и тока.
• Магнитный момент контура с током
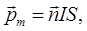
где 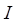 – сила тока в контуре;
– сила тока в контуре; 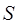 – площадь, охватываемая контуром;
– площадь, охватываемая контуром; 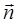 – единичный вектор нормали к поверхности
– единичный вектор нормали к поверхности 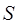 , ограниченной контуром с током (направление
, ограниченной контуром с током (направление 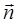 определяется по правилу буравчика).
определяется по правилу буравчика).
• Вращательный момент, действующий на контур с током, помещенный в магнитное поле,
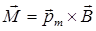 , или
, или 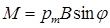 ,
,
где 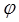 – угол между векторами
– угол между векторами 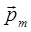 и
и 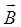 .
.
• Сила 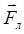 , действующая на заряд q, движущийся со скоростью
, действующая на заряд q, движущийся со скоростью 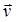 в магнитном поле (сила Лоренца),
в магнитном поле (сила Лоренца),
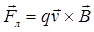 , или
, или 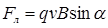 ,
,
где 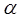 – угол между векторами
– угол между векторами 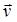 и
и 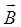 .
.
• Поток вектора магнитной индукции 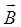 (магнитный поток);
(магнитный поток);
а) в случае произвольной поверхности S и неоднородного поля 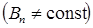
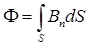 ,
,
где 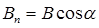 - проекция вектора
- проекция вектора 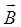 на направление нормали
на направление нормали 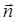 к элементу поверхности dS (
к элементу поверхности dS ( 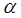 – угол между векторами
– угол между векторами 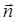 и
и 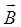 );
);
б) в случае однородного поля и плоской поверхности, расположенной перпендикулярно вектору 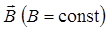 ,
,
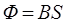 .
.
• Полный поток магнитной индукции, сцепленный с витками контура (потокосцепление),
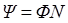 ,
,
где 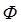 – магнитный поток через один виток;
– магнитный поток через один виток; 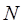 – число витков контура.
– число витков контура.
• Работа но перемещению контура с током в магнитном поле
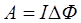 ,
,
где 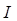 – сила тока в контуре;
– сила тока в контуре; 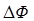 – изменение магнитного потока через поверхность, ограниченную замкнутым контуром (в случае перемещения проводника в магнитном поле
– изменение магнитного потока через поверхность, ограниченную замкнутым контуром (в случае перемещения проводника в магнитном поле 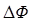 – поток, «заметаемый» проводником при перемещении).
– поток, «заметаемый» проводником при перемещении).
Методические указания и примеры решения задач
При решении задач по данной теме необходимо:
· показать на рисунке направление сил, действующих со стороны магнитного поля на проводник с током или движущийся заряд;
· помнить, что сила, действующая со стороны магнитного поля на проводник с током или движущийся заряд, всегда перпендикулярна направлению вектора магнитной индукции;
· для определения направления силы применять правило левой руки: если левую руку расположить так, чтобы перпендикулярная проводнику составляющая вектора магнитной индукции входила в ладонь, а четыре вытянутых пальца указывали на направление движения положительных зарядов (по току), то отогнутый на 90° большой палец покажет направление силы;
· при наличии нескольких полей или сил различной природы использовать принцип суперпозиции;учитывать различное направление сил со стороны электрического и магнитного полей, действующих на движущийся заряд;
§ в случае равновесия системы проводников с током или зарядов использовать для каждого из них общие условия равновесия: 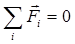 ,
, 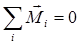 .
.
Пример 2.8. В однородном магнитном поле (В = 0,02 Тл) в плоскости, перпендикулярной линиям индукции, расположено проволочное полукольцо длиной 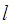 = 3 см, по которому течет ток
= 3 см, по которому течет ток 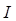 = 0,1 А. Найти силу, действующую на полукольцо, если подводящие провода находятся вне поля.
= 0,1 А. Найти силу, действующую на полукольцо, если подводящие провода находятся вне поля.
Дано: В = 0,02 Тл, l= 3 см, I = 0,1 A; F- ?
Решение
Согласно закону Ампера сила 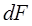 , действующая на элемент тока
, действующая на элемент тока 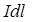 со стороны магнитного поля В, определяется по формуле
со стороны магнитного поля В, определяется по формуле 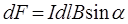 , где
, где 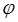 – угол между направлением поля
– угол между направлением поля 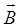 и тока
и тока 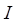 , равный по условию задачи 90°. Поэтому
, равный по условию задачи 90°. Поэтому 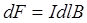 . Направление силы
. Направление силы 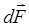 , определяемое по правилу левой руки, показано на рис.2.
, определяемое по правилу левой руки, показано на рис.2.
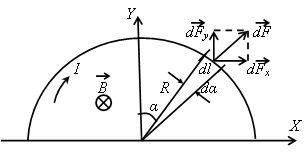
Рис.2.
При переходе от одного элемента полукольца к другому направление элементарных сил, оставаясь радиальным, непрерывно меняется. Поэтому искомую результирующую силу F будем искать по формуле 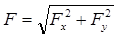 , где
, где 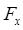 и
и 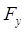 - проекции силы F на координатные оси X и Y. Эти проекции определяются интегрированием:
- проекции силы F на координатные оси X и Y. Эти проекции определяются интегрированием:
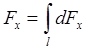 ,
, 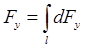 ,
,
где dFx и dFy – проекции элементарных сил dF на координатные оси, символ 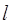 указывает на то, что интеграл берется по всей длине полукольца. Учитывая симметрию полукольца, имеем
указывает на то, что интеграл берется по всей длине полукольца. Учитывая симметрию полукольца, имеем 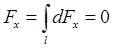 . Тогда результирующая сила
. Тогда результирующая сила
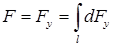 . (1)
. (1)
Из рис.2 следует 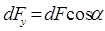 , или, после подстановки
, или, после подстановки 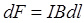 ,
, 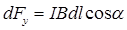 . Поскольку
. Поскольку 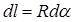 , где
, где 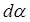 – угол, стягиваемый дугой dl, то
– угол, стягиваемый дугой dl, то 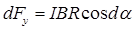 . Теперь введем dFy под знак интеграла (1) и проинтегрируем по
. Теперь введем dFy под знак интеграла (1) и проинтегрируем по 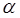 в пределах от
в пределах от 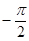 до
до 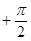 :
:
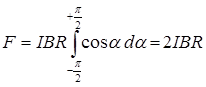 .
.
Подставив в правую часть полученного равенства 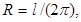 получим окончательно
получим окончательно
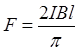 . (2)
. (2)
Проверим, дает ли правая часть (2) единицу силы (Н):
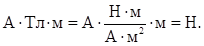
Подставив значения величин в (2), найдем 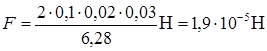 .
.
Согласно выражению (1) сила F направлена вдоль оси Х. Заметим, что если полукольцо распрямить, то все элементарные силы 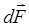 будут направлены вдоль оси Y, что приведет к увеличению результирующей силы; если же полукольцо превратить в кольцо, то последнее будет растягиваться или сжиматься в зависимости от направления тока в кольце.
будут направлены вдоль оси Y, что приведет к увеличению результирующей силы; если же полукольцо превратить в кольцо, то последнее будет растягиваться или сжиматься в зависимости от направления тока в кольце.
Пример 2.9. Рядом с бесконечно длинным проводом, по которому течет ток силы 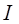 = 5 А, расположена квадратная рамка со стороной
= 5 А, расположена квадратная рамка со стороной 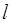 = 10 см и током
= 10 см и током 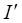 = 0,2 А. Рамка лежит в одной плоскости с проводником, так, что ее сторона, ближайшая к проводу находится от него на расстоянии а = 5 см, ток в ней противоположен по направлению току
= 0,2 А. Рамка лежит в одной плоскости с проводником, так, что ее сторона, ближайшая к проводу находится от него на расстоянии а = 5 см, ток в ней противоположен по направлению току 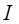 в проводе (см. рис.). Определить работу при удалении рамки из магнитного поля. Считать, что при движении рамки токи
в проводе (см. рис.). Определить работу при удалении рамки из магнитного поля. Считать, что при движении рамки токи 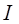 и
и 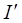 поддерживаются постоянными.
поддерживаются постоянными.
Дано: 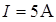 ,
, 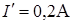 ,
, 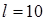 см,
см, 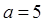 см ;
см ; 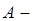 ?
?
Решение
Рассмотрим два способа решения задачи.
Первый способ Квадратная рамка с током 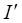 находится в неоднородном магнитном поле прямого проводника с током
находится в неоднородном магнитном поле прямого проводника с током 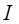 . Индукция этого поля
. Индукция этого поля
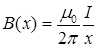 (1)
(1)
где x – расстояние от проводника до рассматриваемой точки поля.
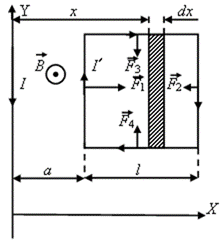
Сила, с которой поле действует на каждую сторону рамки, может быть определена суммированием элементарных сил Ампера
dF = I′ dlBsinα, (2)
где 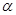 – угол между направлениями тока и поля.
– угол между направлениями тока и поля.
Направление сил, действующих на стороны рамки, определим по правилу левой руки. Учитывая, что для всех элементов одной и той же стороны рамки (левой или правой) величина индукции одинакова и sinα = 1, найдем силы, действующие на каждую из этих сторон:
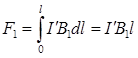 ,
, 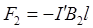 . (3)
. (3)
Что касается других сторон рамки (верхней и нижней), то поскольку они расположены одинаково по отношению к длинному проводу и токи в них противоположны по направлению, то действующие на них силы F 3 и F 4 должны быть уравновешенными. Следовательно, равнодействующая всех сил, приложенных к рамке, равна 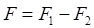 и направлена так, что рамка будет выталкиваться из поля. Используя выражения (1) и (3), представим силы
и направлена так, что рамка будет выталкиваться из поля. Используя выражения (1) и (3), представим силы 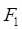 и
и 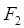 в следующем виде
в следующем виде
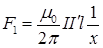
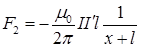 (4)
(4)
Работа выталкивания рамки из магнитного поля складывается из положительной работы силы 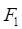 и отрицательной работы силы
и отрицательной работы силы 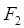 :
:
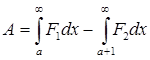 (5)
(5)
При вычислении работы А учтем, что сила 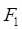 , переместив левую сторону рамки на расстояние
, переместив левую сторону рамки на расстояние 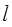 , при дальнейшем перемещении совершает такую же работу, как и сила
, при дальнейшем перемещении совершает такую же работу, как и сила 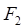 на всем пути перемещения правой стороны рамки, но с противоположным знаком. Таким образом,
на всем пути перемещения правой стороны рамки, но с противоположным знаком. Таким образом,
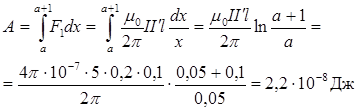
Второй способ. Для определения работ А можно воспользоваться формулой
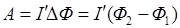 , (6)
, (6)
где 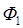 и
и 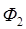 – магнитные потоки через площадь, ограниченную контуром, до и после ее перемещения. Поскольку вне поля магнитный поток через рамку Ф2 = = 0, то (6) принимает следующий вид:
– магнитные потоки через площадь, ограниченную контуром, до и после ее перемещения. Поскольку вне поля магнитный поток через рамку Ф2 = = 0, то (6) принимает следующий вид:
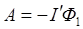 (7)
(7)
Поток 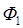 найдем по формуле:
найдем по формуле:
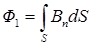 ,
,
где 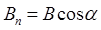 – проекция вектора
– проекция вектора 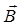 на нормаль к плоскости рамки. Поскольку вектор
на нормаль к плоскости рамки. Поскольку вектор 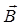 магнитного поля длинного провода перпендикулярен плоскости рамки и составляет угол
магнитного поля длинного провода перпендикулярен плоскости рамки и составляет угол 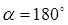 с ее нормалью, то
с ее нормалью, то 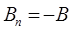 . Следовательно, поток
. Следовательно, поток 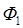 является отрицательным, а изменение потока
является отрицательным, а изменение потока 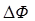 и работа, выражаемая формулой (6) – положительны. При вычислении
и работа, выражаемая формулой (6) – положительны. При вычислении 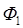 следует иметь в виду, что поле, в котором расположена рамка, неоднородно, т.е. зависит от
следует иметь в виду, что поле, в котором расположена рамка, неоднородно, т.е. зависит от 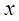 :
: 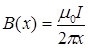 . Следовательно, элементарный поток
. Следовательно, элементарный поток 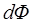 также будет зависеть от x:
также будет зависеть от x: 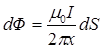 , где
, где 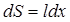 – площадь элементарной полоски длиной
– площадь элементарной полоски длиной 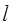 и шириной
и шириной 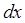 (полоска расположена параллельно длинному проводу). Тогда полный поток
(полоска расположена параллельно длинному проводу). Тогда полный поток
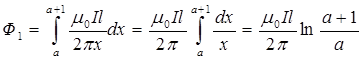
Подставив полученное выражение Ф в формулу (7), найдем
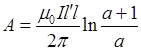
Этот результат совпадает с ответом, полученным первым способом.
Заметим, что в рассмотренном случае работа совершается за счет сил Ампера, действующих в плоскости рамки и выталкивающих рамку из магнитного поля, создаваемого длинным проводом с током. В действительности рамка находится в неустойчивом равновесии и при малейшем его нарушении может развернуться на 180°, после чего начнет притягиваться к длинному проводу. Однако в этом случае рамка будет двигаться так, что магнитный поток через нее будет увеличиваться 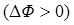 . Можно убедиться, что формула (6) справедлива для расчета работы по перемещению контура любой формы, в произвольном по конфигурации магнитном поле и произвольном перемещении. В случае проводника конечных размеров формула (6) тоже считается справедливой, усложняется лишь расчет величины
. Можно убедиться, что формула (6) справедлива для расчета работы по перемещению контура любой формы, в произвольном по конфигурации магнитном поле и произвольном перемещении. В случае проводника конечных размеров формула (6) тоже считается справедливой, усложняется лишь расчет величины 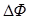 .
.
Основные понятия и формулы
Явление электромагнитной индукции заключается в том, что при любом изменении магнитного потока 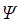 , сцепленного с данным контуром, в последнем возникает электродвижущая сила индукции
, сцепленного с данным контуром, в последнем возникает электродвижущая сила индукции 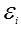 . Явление электромагнитной индукции описывается законом Фарадея и правилом Ленца.
. Явление электромагнитной индукции описывается законом Фарадея и правилом Ленца.
• Закон Фарадея. Величина ЭДС индукции пропорциональна скорости изменения магнитного потока:
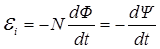 ,
,
где 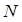 – число витков контура; Ф – поток через один виток;
– число витков контура; Ф – поток через один виток; 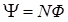 – потокосцепление; знак минус связан с правилом Ленца, определяющим направление тока индукции.
– потокосцепление; знак минус связан с правилом Ленца, определяющим направление тока индукции.
• Правило Ленца. ЭДС индукции, а, следовательно, и индукционный ток в контуре всегда имеют такое направление, что магнитное поле индуцированного тока препятствует тем изменениям основного потока магнитного поля, которые вызвали появление индукционного тока.
• Потокосцепление контура
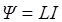 , где
, где 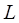 – индуктивность;
– индуктивность; 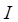 – сила тока в контуре.
– сила тока в контуре.
• Индуктивность соленоида с немагнитным сердечником 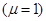
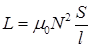 ,
,
где 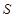 ,
, 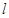 - соответственно, площадь поперечного сечения и длина соленоида.
- соответственно, площадь поперечного сечения и длина соленоида.
Ток индукции в контуре с сопротивлением R
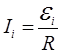 .
.
• Полный заряд, протекающий по контуру за время 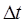 изменения магнитного потока,
изменения магнитного потока,
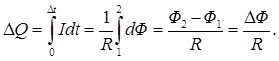 .
.
• ЭДС индукции на концах проводника, движущеюся с постоянной скоростью 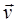 в магнитном поле с индукцией
в магнитном поле с индукцией 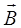 ,
,
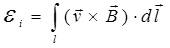 ,
,
где 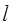 – длина проводника.
– длина проводника.
• Энергия магнитного поля, связанного с контуром индуктивностью L, по которому течет ток 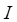 ,
,
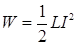 .
.
Методические указания и примеры решения задач
При решении задач на данную тему необходимо:
§ применять закон Фарадея при любом изменении магнитного потока через поверхность, ограниченную проводящим контуром, или перемещении проводника в магнитном поле;
§ учитывать, что величина ЭДС индукции определяется скоростью изменения магнитного потока и не зависит от величины потока;
§ иметь в виду, что закон сохранения энергии выполняется для любых физических процессов и явлений: не составляет исключение и явление электромагнитной индукции: получение тока индукции всегда связано с работой, которую необходимо совершить, чтобы тем или иным способом изменить потокосцепление.
Анализ задачи следует начинать с определения причин, вызвавших изменение магнитного потока или причин перераспределения зарядов. Это позволяет найти по правилу Ленца знак ЭДС индукции и направление тока индукции. Если дан замкнутый контур, поток через который изменяется по тем или иным причинам, то его следует выразить как функцию времени. Тогда ЭДС индукции может быть найдена путем последующего дифференцирования этой функции. Если дан проводник и в задаче требуется найти разность потенциалов на концах проводника, движущегося в магнитном ноле, то надо иметь в виду, что искомая разность потенциалов численно равна ЭДС индукции в проводнике. В этом случае, в зависимости от условия задачи, ЭДС индукции находят либо тоже по формуле, выражающей закон Фарадея, где под 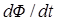 следует понимать магнитный поток, пересекаемый движущимся проводником в единицу времени, либо исследуя силы Лоренца, действующие на свободные заряды в движущемся проводнике.
следует понимать магнитный поток, пересекаемый движущимся проводником в единицу времени, либо исследуя силы Лоренца, действующие на свободные заряды в движущемся проводнике.
Пример 2.10. Рамка площадью 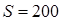 см
см 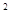 равномерно вращается с частотой
равномерно вращается с частотой 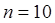 с
с 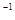 относительно оси, лежащей в плоскости рамки. Ось вращения перпендикулярна линиям индукции однородного магнитного поля
относительно оси, лежащей в плоскости рамки. Ось вращения перпендикулярна линиям индукции однородного магнитного поля 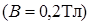 . Каково максимальное и среднее значения ЭДС индукции за время, в течение которого магнитный поток, пронизывающий рамку, изменится от максимального значения до нуля?
. Каково максимальное и среднее значения ЭДС индукции за время, в течение которого магнитный поток, пронизывающий рамку, изменится от максимального значения до нуля?
Дано: 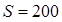 см
см 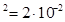 м
м 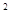 ,
, 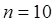 с
с 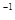 ,
, 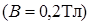 ;
; 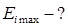
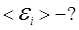
Решение
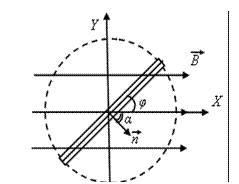
На рисунке показано мгновенное положение рамки под углом φ к направлению магнитного поля. Угол между нор-малью к рамке и направлением магнитного поля, как видно из рисунка, 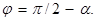 Поэтому поток, пронизывающий рам-ку,
Поэтому поток, пронизывающий рам-ку, 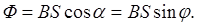 Учитывая, что за время
Учитывая, что за время 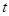 угол поворота
угол поворота 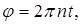 где n – частота вращения рамки (число оборотов, совершаемых рамкой за 1 с), для изменения потока со временем можно записать
где n – частота вращения рамки (число оборотов, совершаемых рамкой за 1 с), для изменения потока со временем можно записать
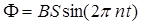 . (1)
. (1)
Согласно закону Фарадея ЭДС индукции определяется скоростью изменения потока:
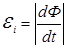 . (2)
. (2)
Подставив в формулу (2) выражение (1) и продифференцировав по времени, найдем зависимость мгновенного значения ЭДС индукции от времени:
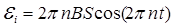 . (3)
. (3)
 Максимальное значение ЭДС (амплитуда):
Максимальное значение ЭДС (амплитуда):
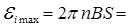
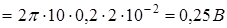
Для нахождения среднего значения ЭДС индукции следует воспользоваться формулой
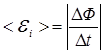
где 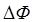 – изменение магнитного потока за время
– изменение магнитного потока за время 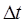 поворота рамки из положения, при котором рамка параллельна магнитному полю в положение, при котором она перпендикулярна ему. За это время рамка повернется на угол
поворота рамки из положения, при котором рамка параллельна магнитному полю в положение, при котором она перпендикулярна ему. За это время рамка повернется на угол 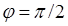 . Поток при этом изменится от значения Ф1 = 0 до значения Ф2 = BS. Изменение потока за это время составит ΔФ = BS. Время Δt найдем из условия
. Поток при этом изменится от значения Ф1 = 0 до значения Ф2 = BS. Изменение потока за это время составит ΔФ = BS. Время Δt найдем из условия 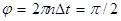 . Отсюда получаем
. Отсюда получаем 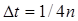 . Следовательно, искомое среднее значение ЭДС индукции
. Следовательно, искомое среднее значение ЭДС индукции
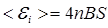 . (4)
. (4)
Убедимся в том, что правая часть полученной расчетной формулы дает единицу ЭДС вольт (В):
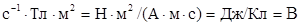 .
.
Производя вычисления по формуле (4), получим
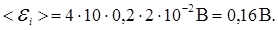
Задачи данного параграфа связаны с расчетом магнитного поля при наличии магнитных сред и базируются на знании свойств диа-, пара- и ферромагнетиков. Расчет полей значительно упрощается введением вектора напряженности 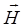 , как характеристики магнитного поля, определяемой через векторы
, как характеристики магнитного поля, определяемой через векторы 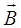 и
и 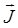 соотношением
соотношением 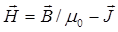 . Особенность вектора
. Особенность вектора 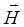 состоит в том, что его циркуляция не зависит от магнитных свойств среды, в которой находится выбранный контур интегрирования, а определяется лишь алгебраической суммой токов проводимости, охватываемых этим контуром. Вектор
состоит в том, что его циркуляция не зависит от магнитных свойств среды, в которой находится выбранный контур интегрирования, а определяется лишь алгебраической суммой токов проводимости, охватываемых этим контуром. Вектор 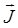 – магнитный момент, возникающий при намагничивании среды. Вектор
– магнитный момент, возникающий при намагничивании среды. Вектор 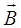 характеризует магнитное поле с учетом влияния среды.
характеризует магнитное поле с учетом влияния среды.
При решении уравнения, полученного в результате применения теоремы о циркуляции вектора 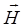 , часто используется соотношение
, часто используется соотношение 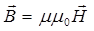 . При этом важно обращать внимание на то, что относительная магнитная проницаемость
. При этом важно обращать внимание на то, что относительная магнитная проницаемость 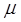 ферромагнетика сама зависит от
ферромагнетика сама зависит от 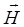 и является величиной переменной.
и является величиной переменной.
Важно также, что магнитные свойства сердечника зависят от его формы. В рассматриваемых ниже решениях задач это показано на примере сердечников, имеющих форму тора сплошного или с узким воздушным зазором.
Интерференция света
Основные понятия и формулы
Интерференция света — усиление или ослабление света в результате сложения двух (или нескольких) световых волн с одинаковыми частотами и с независящей от времени разностью фаз (такие волны называют когерентными).
· Оптическая разность хода D двух лучей, один из которых проходит путь длиной l1 в среде с показателем преломления n1, а с другой - путь l2 в среде с показателем преломления n2
D = l2n2 – l1n1.
· Условие максимального усиления света (интерференционные максимумы)
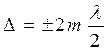 ,
,
где m = 0,1,2,...; l – длина волны.
· Условие максимального ослабления света (интерференционные минимумы)
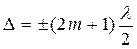 ,
,
где m = 0,1,2,..; l – длина волны.
· Оптическая разность хода лучей в тонких пленках в отраженном свете
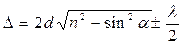 ,
,
где d – толщина пленки; n – показатель преломления вещества пленки; a – угол падения. 
· Радиусы темных колец Ньютона в отраженном свете
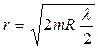 ,
,
где m = 1,2,3,... – порядковый номер кольца, R – радиус кривизны линзы.
· Радиусы светлых колец Ньютона в отраженном свете
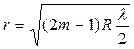 ,
,
где m = 1,2,3,... – порядковый номер кольца, R – радиус кривизны линзы.
Методические указания и примеры решения задач
В качестве общего подхода к решению задач на интерференцию света используются следующие действия:
1) выясняются причины появления оптической разности хода между интерферирующими лучами и находится эта разность;
2) записываются условия интерференционных максимумов или минимумов;
3) из этих условий и определяется искомая величина.
Задачи на интерференцию света в основном делятся на две группы.
К задачам первой группы относятся случаи интерференции, полученной с помощью зеркала Ллойда, зеркал Френеля, бипризмы Френеля, в опыте Юнга др. В этих задачах для расчета интерференционной картины удобно данную оптическую систему заменить другой, эквивалентной, считая при этом, что имеется не один, а два когерентных источника.
Вторую группу составляют задачи на интерференцию в плоскопараллельных, клинообразных тонких слоях, а также задачи на кольца Ньютона.
При решении этих задач следует обратить внимание на то, что разность фаз когерентных волн при встрече, и, следовательно, результат интерференции, обусловлены двумя причинами: оптической разностью хода и условиями отражения обеих волн.
Если отражение происходит от границы с оптически более плотной средой, фаза волны претерпевает изменение на π. Если отражение происходит от границы с оптически менее плотной средой, то скачка фазы не происходит.
Пример 2.11 На толстую стеклянную пластинку с показателем преломления 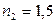 , покрытую тонким слоем пленки с показателем преломления
, покрытую тонким слоем пленки с показателем преломления 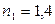 , под углом
, под углом 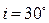 падает пучок лучей монохроматического света с длиной волны
падает пучок лучей монохроматического света с длиной волны 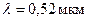 . Определить минимальную толщину пленки, если отраженный свет максимально ослаблен.
. Определить минимальную толщину пленки, если отраженный свет максимально ослаблен.
Дано: 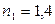 ,
, 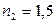 ,
, 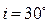 ,
, 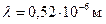 ;
; 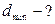
Решение
На границу раздела воздух-пленка падает плоская монохроматическая волна, угол падения которой 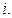 На границе раздела волна частично отражается, частично преломляется. Волны, отраженные от верхней поверхности пластинки и отраженные от нижней и затем преломленные на верхней, будут когерентными и при наложении интерферируют.
На границе раздела волна частично отражается, частично преломляется. Волны, отраженные от верхней поверхности пластинки и отраженные от нижней и затем преломленные на верхней, будут когерентными и при наложении интерферируют.
Результат интерференции зависит от того, какому условию удовлетворяет оптическая разность хода.
Отраженный свет максимально ослаблен, следовательно, при интерференции выполняется условие минимума:
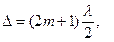 где
где 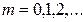
Оптическая разность хода указанных волн
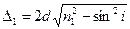 .
.
Волна, отраженная от верхней поверхности пленки, изменяет фазу на π и точно также на π изменится фаза волны, отраженной от нижней поверхности пленки. Поэтому добавочная разность фаз и разность хода не возникает 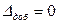 .
.
Таким образом, оптическая разность хода указанных волн
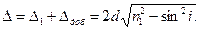
Условие минимума освещенности:
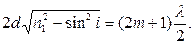
Найдем толщину пленки d:
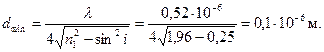
Пример 2.12 При освещении клина с углом 2,2·10–4 рад пучком параллельных лучей с длиной волны 0,66 мкм, падающим нормально к поверхности, образуются интерференционные полосы, причем на длине 1 см, укладываются 10 темных полос. Определить показатель преломления материала пластины.
Дано: α = 2,2·10–4 рад, λ = 0,66 мкм, l = 10–2 м, Ν = 10; n = ?
Решение
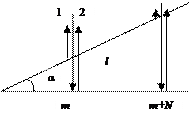 В данном случае интерферируют лучи 1 и 2 отраженные от двух поверхностей клина (рис. ). Так как интерференция на клине наблюдается при малых углах α, лучи 1 и 2 можно считать параллельными.
В данном случае интерферируют лучи 1 и 2 отраженные от двух поверхностей клина (рис. ). Так как интерференция на клине наблюдается при малых углах α, лучи 1 и 2 можно считать параллельными.
Оптическую разность хода лучей можно определить по формуле 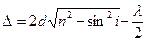 , учтя, что при нормальном падении лучей на пластину i = 0. Условие m-го интерференционного минимума может быть записано в виде
, учтя, что при нормальном падении лучей на пластину i = 0. Условие m-го интерференционного минимума может быть записано в виде
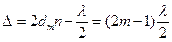 , или
, или 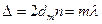 ,
,
где 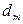 – толщина клина в том месте, где наблюдается темная полоса, соответствующая номеру m.
– толщина клина в том месте, где наблюдается темная полоса, соответствующая номеру m.
Пусть темной полосе m + N соответствует толщина 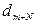 . Тогда
. Тогда 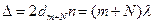 . Согласно условию задачи на расстоянии l укладывается Ν полос. Из рисунка видно, что
. Согласно условию задачи на расстоянии l укладывается Ν полос. Из рисунка видно, что 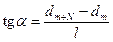 . Учитывая, что при малых углах
. Учитывая, что при малых углах 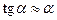 и подставляя значения
и подставляя значения 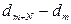 , получим
, получим 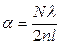 .
.
Отсюда находим показатель преломления
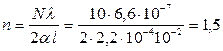 .
.
Дифракция света
Основные понятия и формулы
Дифракция света — явления, связанные с отклонением светового луча от прямолинейности при распространении света в среде с резкими неоднородностями.
· Радиусы зон Френеля для сферического волнового фронта
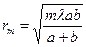 , (1)
, (1)
где m = 1,2,3,... – порядковый номер зоны; l – длина волны света; a – расстояние от источника света до сферического фронта волны; b – расстояние от сферического фронта волны до точки наблюдения.
Элементы квантовой механики
Основные понятия и формулы
· Длина волны де Бройля
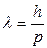 ,
,
где р – импульса частица.
· Соотношение неопределенностей Гейзенберга
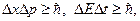
где Δх – неопределенность координаты; Δр – неопреде-ленность импульса; ΔЕ – неопределенность энергии; Δt – неопределенность времени.
Методические указания и примеры решения задач
Пример 2.18 Найти длину волны де Бройля для электрона, обладающего кинетической энергией: 1) Т = 100 эВ; 2) Т =3 МэВ.
Дано: Т =100 эВ; Т =3 МэВ; λ =?
Решение
Поскольку длина волны де Бройля 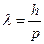 , то задача сводится к выражению импульса p электрона через его кинетическую энергию Т. Решение задачи зависит от того, классической или релятивистской частицей следует считать электрон.
, то задача сводится к выражению импульса p электрона через его кинетическую энергию Т. Решение задачи зависит от того, классической или релятивистской частицей следует считать электрон.
1.В первом случае Т << moc2, где moc2 =0,51 МэВ – энергия покоя электрона, то электрон является классической частицей, его импульс и кинетическая энергия связаны соотношением: 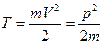 . Отсюда
. Отсюда 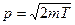 , подставив его в формулу длины волны де Бройля, получим:
, подставив его в формулу длины волны де Бройля, получим:
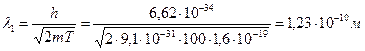 .
.
2.Во втором случае 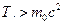 , поэтому электрон следует считать релятивистской частицей, для которой импульс и энергия связаны:
, поэтому электрон следует считать релятивистской частицей, для которой импульс и энергия связаны:
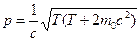 . Тогда для дебройлевской длины волны получим выражение:
. Тогда для дебройлевской длины волны получим выражение:
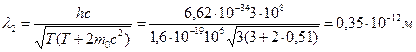
Пример 2.19 Электрон с кинетической энергией Т= 4 эВ локализован в области размером l=1 мкм. Оценить с помощью соотношения неопределенностей относительную неопределенность его скорости.
Дано: Т= 4 эВ= 4·1,6·10-19 = 6,4·10-19 Дж, l=10-6 м.
Решение
Полагая в соотношении неопределенностей 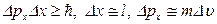 , получаем для неопределен-ности модуля скорости электрона формулу
, получаем для неопределен-ности модуля скорости электрона формулу 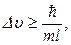 где m – масса электрона. Учитывая, что по условию задачи
где m – масса электрона. Учитывая, что по условию задачи 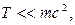 находим
находим 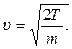 Таким образом, для относительной неопределенности модуля скорости электрона получаем оценку
Таким образом, для относительной неопределенности модуля скорости электрона получаем оценку 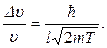 Подставляя численные значения величин, находим
Подставляя численные значения величин, находим 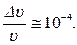
Контрольная работа №2
Электростатика и постоянный ток
Электростатическое поле
Основные понятия и формулы
Электростатика изучает электрическое поле неподвижных зарядов (дискретных и однородно распределенных)
- Закон Кулона
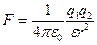 ,
,
где F – сила взаимодействия двух точечных зарядов q1 и q2 на расстоянии r; ε – диэлектрическая проницаемость среды (безразмерная величина, ε = 1 в вакууме); ε0 = 8,85·10-12Ф/м – электрическая постоянная. Фарада – единица электроемкости.
· Закон сохранения заряда 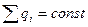 означает, что алгебраическая
означает, что алгебраическая
сумма электрических зарядов изолированной системы сохраняется.
· Напряженность электрического поля 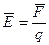 - это сила, действующая со стороны пволя на единичный точечный заряд, помещенный в данную точку поля.
- это сила, действующая со стороны пволя на единичный точечный заряд, помещенный в данную точку поля.
· Напряженность поля точечного заряда в вакууме 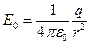 .
.
В диэлектрике 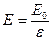 , где
, где 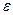 - диэлектрическая проницаемость диэлектрика, а
- диэлектрическая проницаемость диэлектрика, а 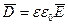 - вектор электрического смещения.
- вектор электрического смещения.
· Циркуляция вектора E по замкнутому контуру L: 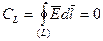 .
.
· Работа электростатической силы по замкнутому контуру 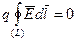 .
.
· Поток вектора E через замкнутую поверхность 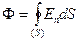 , где En – проекция
, где En – проекция 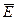 на нормаль
на нормаль 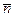 к элементу поверхности dS
к элементу поверхности dS
· Теорема Остроградского-Гаусса 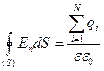 , где
, где 
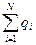 - алгебраическая сумма зарядов внутри замкнутой поверхности S.
- алгебраическая сумма зарядов внутри замкнутой поверхности S.
· Принцип суперпозиции электрических полей
Напряженность поля двух и более точечных зарядов в данной точке пространства равна геометрической сумме напряженностей, создаваемых этими зарядами, т.е. 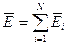
· Напряженность поля бесконечно длинной равномерно заряженной нити на расстоянии r от ее оси, 

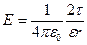 , где τ – линейная плотность заряда т.е. заряд единицы длины [Кл / м] .
, где τ – линейная плотность заряда т.е. заряд единицы длины [Кл / м] .
· Напряженность поля металлической сферы радиусом R, несущей заряд Q, на расстоянии r от центра сферы:
E = 0 (при r < R);
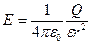 (при r>R);
(при r>R);
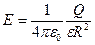 (при r = R).
(при r = R).
· Напряженность поля бесконечной равномерно заряженной плоскости
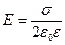 , где σ – поверхностная плотность заряда, т.е. заряд единицы площади [Кл/м2].
, где σ – поверхностная плотность заряда, т.е. заряд единицы площади [Кл/м2].
Методические указания и примеры решения задач
Метод расчета электростатического поля выбирается в зависимости от того, как распределены заряды в пространстве.
- Электрическое поле системы точечных зарядов вычисляется методом суперпозиции полей:
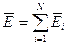 .
.
2. Поля однородного распределения зарядов на телах симметричной формы (плоскостях, нитях, сферах, шарах, цилиндрах и т. д.) вычисляются методом Гаусса. Реализация метода начинается с записи теоремы Гаусса 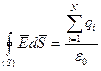 ,затем выбирается поверхность, согласованная с симметрией заряженного тела, т.е. поверхность S должна быть геометрическим местом точек, для которых E=const . Тогда поток
,затем выбирается поверхность, согласованная с симметрией заряженного тела, т.е. поверхность S должна быть геометрическим местом точек, для которых E=const . Тогда поток 
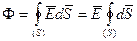 . Далее подсчитав заряды внутри этой поверхности по теореме Гаусса определяют E.
. Далее подсчитав заряды внутри этой поверхности по теореме Гаусса определяют E.
3. Поля однородного распределения зарядов любой симметрии вычисляют методом дифференцирования-интегрирования (ДИ), при этом используется принцип суперпозиции электрических полей, созданных квазиточечными зарядами. Реализация метода ДИ осуществляется в три этапа:
a) Анализ задачи и запись нужного физического закона (например, закона Кулона, или формулы для E ) в дифференциальной форме. Это расширяет область использования закона (формулы), позволяя применить его (их) к неточечным зарядам.
b) Подготовка дифференциальной формы (пункт а)) к интегрированию: выбор удобной переменной интегрирования, учет симметрии задачи и т.п.
c) Интегрирование рабочей формулы 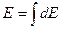 ,
, 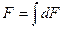 и т. д.
и т. д.
Пример 2.1.
Использовать метод Гаусса для нахождения напряженности 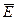 поля равномерно заряженной нити с линейной плотностью τ (Кл/м).
поля равномерно заряженной нити с линейной плотностью τ (Кл/м).
Дано: τ ; Eнити(r) - ?
Решение: Выбираем замкнутую поверхность Гаусса в виде цилиндра длиной l и радиусом r, соосного с нитью. В силу осевой (аксиальной) симметрии величина напряженности E будет одинаковой в любой точке боковой поверхности цилиндра. Поэтому поток напряженности через замкнутую цилиндрическую поверхность S будет 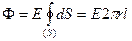 , так как поток
, так как поток 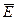 через основания цилиндра равен 0, а суммарный заряд внутри S равен τ l, то по теореме Гаусса
через основания цилиндра равен 0, а суммарный заряд внутри S равен τ l, то по теореме Гаусса 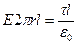 или
или 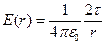 .
.
Анализ результата: полученное выражение показывает, что поле вокруг нити неоднородно 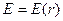 , в отличие, например, от поля однородно заряженной плоскости. /Уместно упомянуть о сходстве полученной формулы с выражением индукции магнитного поля прямого тока I:
, в отличие, например, от поля однородно заряженной плоскости. /Уместно упомянуть о сходстве полученной формулы с выражением индукции магнитного поля прямого тока I: 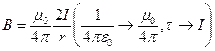 .
.
Пример 2.2.
Определить напряженность поля отрезка однородно заряженной нити в точке О, не лежащей против середины данного отрезка и находящейся на расстоянии r0 от него. Линейная плотность заряда нити τ, длина нити l.
Дано : l, τ , r0, Eo(ro) - ?
Решение: Равномерная заряженность отрезка нити и отсутствие высокой симметрии (центральной и аксиальной) в задаче заставляют обратиться к методу ДИ. Выделим на отрезке квазиточечный заряд dq = τ dl и определим поле dE0 этого заряда в точке 0. Искомая напряженность Eo( ro) получится в результате суперпозиции напряженностей dE0 от всех dl, составляющих отрезок l. Асимметричное расположение точки О относительно концов отрезка приводит к тому, что результирующий вектор Eo( ro) будет иметь составляющие Eox = Eo cosα и Eoy = Eo sinα ,которые определяют интегрированием dEox и dEoy соответственно. Отметим, что при интегрировании линейные переменные необходимо заменить на более удобные угловые т.е. ( r, dl→ α, dα ). Из рассмотрения подобных заштрихованных треугольников получим: 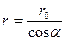 ,
,
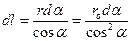 . В результате необходимые для интегрирования dEox и dEoy будут выглядеть следующим образом:
. В результате необходимые для интегрирования dEox и dEoy будут выглядеть следующим образом:
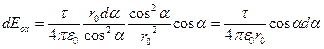 ,
, 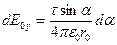 .
.
Третий этап метода ДИ- интегрирование:
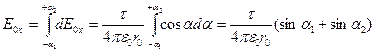
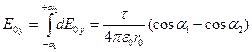
Анализ результата: При α1 =α2=α задача становится симметричной и E0 y =0, а
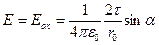 , что на множитель sinα отличается от напряженности поля бесконечной нити. Рассматриваемый отрезок превращается в такую нить при
, что на множитель sinα отличается от напряженности поля бесконечной нити. Рассматриваемый отрезок превращается в такую нить при 
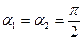 и в этом случае
и в этом случае 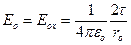 . Таким образом, наш результат позволяет получить известные формулы как частный случай. Это подтверждает его правильность.
. Таким образом, наш результат позволяет получить известные формулы как частный случай. Это подтверждает его правильность.
Потенциал. Работа по перемещению заряда в электростатическом поле.
Основные понятия и формулы.
· Потенциал электростатического поля 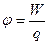 -это потенциальная энергия единичного положительного заряда, помещенного в данную точку поля.
-это потенциальная энергия единичного положительного заряда, помещенного в данную точку поля.
· 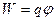 - Потенциальная энергия заряда q в поле с потенциалом φ.
- Потенциальная энергия заряда q в поле с потенциалом φ.
· 
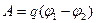 - работа по перемещению заряда q из точки поля с потенциалом φ1 в точку с потенциалом φ2 ; работа сил поля в этом случае может быть также рассчитана
- работа по перемещению заряда q из точки поля с потенциалом φ1 в точку с потенциалом φ2 ; работа сил поля в этом случае может быть также рассчитана 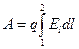 , где El – проекция вектора Е на направление перемещения dl .
, где El – проекция вектора Е на направление перемещения dl .
· Связь напряженности и потенциала электростатического поля
· 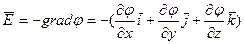 или
или 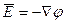 , где
, где 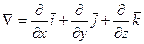 - векторный дифференциальный оператор (Набла ).
- векторный дифференциальный оператор (Набла ).
· Для однородного поля напряженностью E разность потенциалов 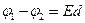 , где d – расстояние между точками с потенциалами φ1 и φ2 .
, где d – расстояние между точками с потенциалами φ1 и φ2 .
· Потенциал электрического поля, создаваемого точечным зарядом Q на расстоянии r от заряда 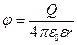 , где ε – диэлектрическая проницаемость среды, окружающей заряд
, где ε – диэлектрическая проницаемость среды, окружающей заряд
· Потенциал электрического поля, создаваемого сферической поверхностью с зарядом Q и радиуса R, в точке удаленной на расстояние r от центра сферы:
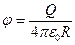 ( при
( при 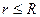 );
);
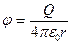 ( при
( при 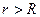 ) .
) .
Видно, что последняя формула совпадает с выражением для потенциала точечного заряда.
· Потенциал электрического поля, создаваемого системой n точечных зарядов согласно принципу суперпозиции электрических полей равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности: 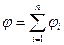 .
.
Методические указания и примеры решения задач
Метод расчета потенциалов электрических полей ,также как и напряженностей, определяется распределением зарядов в пространстве.
Потенциал системы точечных зарядов рассчитывается по принципу суперпозиции.
Потенциал поля непрерывно распределенных зарядов рассчитывается методом не сам потенциал, а разность потенциалов. Так, например, формула 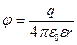 выражает потенциал поля точечного заряда на расстоянии r от него, справедлива в предположении, что потенциал φ=0 при r→∞.
выражает потенциал поля точечного заряда на расстоянии r от него, справедлива в предположении, что потенциал φ=0 при r→∞.
В основе метода определения разности потенциалов лежит соотношение
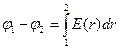 , связывающее разность потенциалов двух точек поля с напряженностью в области между этими точками. Задача такого рода упрощается в случае симметричных полей с заранее известным распределением напряженности E( r).
, связывающее разность потенциалов двух точек поля с напряженностью в области между этими точками. Задача такого рода упрощается в случае симметричных полей с заранее известным распределением напряженности E( r).
Пример2.3 Положительный заряд q равномерно распределен по кольцу радиуса R . Найти потенциал на оси кольца как функцию расстояния h от центра кольца.
Дано: q,R; 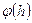 ?
?
Решение: Заряд, распределенный по кольцу , нельзя считать точечным поэтому воспользуемся методом ДИ. Разобьем кольцо на элементарные отрезки dl .Заряд такого отрезка будет 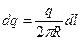 , а потенциал , создаваемый этим зарядом , можно определить по формуле потенциала точечного заряда ,тогда получим:
, а потенциал , создаваемый этим зарядом , можно определить по формуле потенциала точечного заряда ,тогда получим: 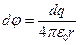 , где r- расстояние от элемента кольца до точки, в которой определяется потенциал,т.е
, где r- расстояние от элемента кольца до точки, в которой определяется потенциал,т.е 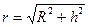
Подставив это выражение в 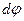 и интегрируя, найдем
и интегрируя, найдем 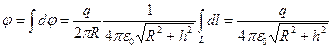 .
.
Анализ полученной функции φ( h) показывает:
- Потенциал поля в произвольной точке на оси кольца зависит от заряда q и не зависит от того является ли распределение заряда по кольцу равномерным или неравномерным;
- Потенциал является положительным для всех значений h и имеет максимальное значение в центре кольца.
Электрическая емкость. Конденсаторы.
Дата: 2019-07-30, просмотров: 338.