последовательно 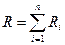, параллельно 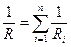, здесь  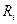- сопротивление  i-го проводника, n - число проводников

· Закон Ома в дифференциальной форме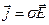

· Закон Ома:

для неоднородного участка цепи ;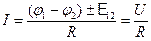

для однородного участка цепи ;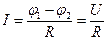

для замкнутой цепи .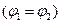

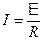Здесь 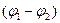-разность потенциалов на концах участка цепи; E₁₂ –ЭДС источников тока, входящих в участок цепи; U-напряжение на участке цепи.

Пример2.5  Два источника с ЭДС E₁=3В и E₂=2В соединены параллельно. Определить разность потенциалов на зажимах источника, если внутреннее сопротивление источников r₁=0,3Ом и r₂=0,2Ом соответственно.

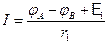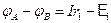Решение: По закону Ома для неоднородного участка цепи АE₁В:  или , где E₁ >0, т.к. направление ЭДС совпадает с направлением тока. На участке BE₂A: 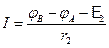, или 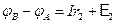, где E₂<0, т.к. направления ЭДС и тока противоположны.По закону Ома для замкнутой цепи 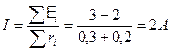, поэтому 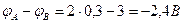, , 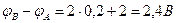что подтверждает правильность расчета тока. Вольтметр ( с большим сопротивлением), включенный между точками А и В, покажет 2,4В.

Правила Кирхгофа

Основные понятия и формулы

При расчете разветвленных электрических цепей постоянного тока пользуются двумя правилами (законами) Кирхгофа.

Первое правило относится к узлам цепей, т.е. к точкам, в которых сходятся не менее трех проводников: алгебраическая сумма сил токов, сходящихся в узле, равна нулю,т.е. 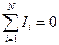 (при этом токи «втекающие» в узел считаются положительными, а «вытекающие» -отрицательными).

Второе правило относится к замкнутым контурам цепей: алгебраическая сумма напряжений на всех участках контура равна алгебраической сумме электродвижущих сил, действующих в нем, т.е 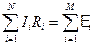.При этом силы токов и ЭДС считаются положительными, если их направление совпадают с выбранным (произвольно) направлением обхода контура.

Пример 2.6. Определить все токи (I₁…I₅) в разветвленной цепи, если заданы R₁…R₅ и E₁…E₅.

Решение. Произвольно выбираем направление токов. Применяем 1-ое правило Кирхгофа к одному из двух узлов (только один независим): 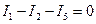. Произвольно выбираем направление обхода в двух контурах (только два из трех контуров независимы). Применяем 2-ое правило Кирхгофа в выбранных контурах:

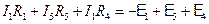
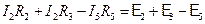
       Таким образом, мы имеем три уравнения для трех неизвестных токов (I₁, I₂, I₅). Получение отрицательного значения какого-либо тока означает, что первоначальный выбор направления этого тока был неправильным и его надо изменить.

Магнитостатика.

Расчет магнитных полей постоянных токов
различной конфигурации

Основные понятия и формулы

• Закон Био - Савара – Лапласа

,

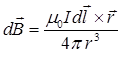где 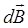 – вектор магнитной индукции, создаваемый элементом тока 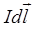; 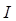– сила тока; 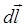– вектор, равный по модулю длине элемента проводника и совпадающий по направлению с током; 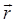– радиус-вектор, проведенный от середины элемента  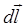в точку, где определяется магнитная индукция; 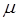– магнитная проницаемость среды;  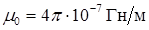- магнитная постоянная .

• Модуль вектора магнитной индукции

,

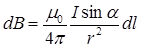где 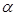 – угол между векторам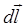и  и .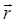

• Принцип суперпозиции магнитных полей

,

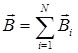где 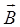 – магнитная индукция результирующего поля;  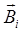– магнитная индукция суммируемых полей:

• Магнитная индукция в центре кругового проводника с током

,

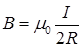где 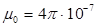Гн/м – магнитная постоянная; 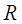– радиус кривизны проводника; 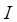– сила тока.

• Магнитная индукция поля в точке, лежащей на оси кругового про­водника с током на расстоянии h от его центра,

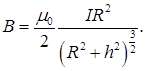
• Магнитная индукция поля, создаваемого участком проводника,

,

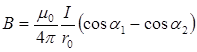где 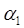 и 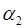 - углы между осью проводника и прямыми, проведенными из концов проводника в точку наблюдения (см. рис. 5).

• Магнитная индукция поля, создаваемого бесконечно длинным пря­мым проводником с током,

,

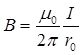 где 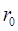 –  расстояние от оси проводника до точки наблюдения.

• Магнитная индукция поля, создаваемого соленоидом в средней его части (или тороидом на его оси),

,

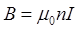где 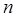- число витков, приходящихся на единицу длины соленоида (тороида); 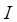- сила тока в одном витке.

Методические указания и примеры решения задач

Математические методы расчета магнитных полей выбираются в зависимости от того, какова конфигурация токов, практически они являются теми же, что и методы расчета электрических полей.

При расчете магнитных полей необходимо:

• указать основные законы и формулы, на которых базируется решение задачи (если при решении задачи применяется формула, имеющая частный харак­тер, не выражающая какой-либо физический закон или определение физи­ческой величины, её следует вывести);
• знать правила изображения магнитных полей: вектор 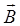 в каждой точке силовой линии направлен по касательной к ней, а густота линий пропорциональна значению 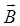; силовые линии магнитной индукции замкнуты, не пересекаются и не соприкасаются;
• применять для определения направления поля правило буравчика: если направление поступательного движения буравчика совпадает с направле­нием тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитной индукции;
• знать, что мнемоническое правило буравчика связано с правилом вектор­ного умножения векторов;
• использовать принцип суперпозиции парциальных (слагаемых) полей: магнитная индукция результирующего поля, создаваемого несколькими токами, равна векторной сумме магнитных индукций полей, создаваемых каждым током в отдельности.

Пример 2.7  Из проволоки длиной 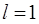м сделана квадратная рамка. По рамке течет ток 1 = 10 А. Найти магнитную индукцию  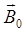в центре рамки.

Дано: 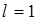 м, 1 = 10 А; - ?

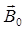Решение

Согласно принципу суперпозиции полей магнитная индукция 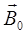 квадратной рамки равна векторной сумме магнитных индукций, создаваемых каждой стороной в отдельности:

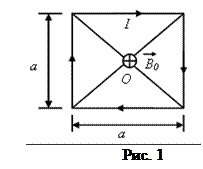
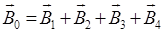. Учитывая, что эти векторы и точке О имеют одинаковое направление и в силу симметрии рамки равны по модулю, имеем 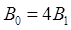. Таким образом, задача нахождения  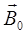сводится к определению магнитной индукции, создаваемой одной из сторон рамки, например 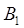. Для определения 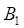запишем сначала в дифференциальной форме основной закон, на котором основано решение задач:

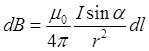
Принимая во внимание, что индукция магнитного поля каждого элемен­та тока 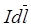 имеет в точке О одно и то же направление, получим

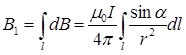
где символ l указывает, что интеграл берется по длине одной стороны рамки. Преобразуем подынтегральное выражение так, чтобы можно было проинтегрировать по углу 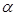. Пусть элемент  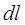виден из точки О под углом 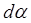. Тогда длина дуги, стягивающей этот угол, 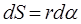. С другой стороны, как это следует из малого прямоугольного треугольника ABC (см. рис.1), можно написать: 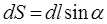. Теперь, учитывая приведенное выражение 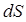, найдем 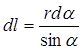. 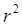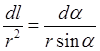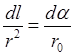Разделив левую и правую части найденного равенства  на , получим  или , где 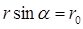. Подставив это выражение под знак интеграла в формуле для магнитной индукции 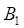, получим

.

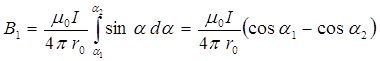Учтем, что угол 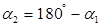; расстояние 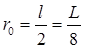. Тогда магнитная индукция, создаваемая одной стороной рамки, 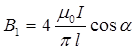, а искомая магнитная индукция 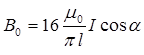. Подставив значения величин, найдем

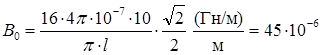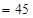Тл мкТл.

Направление вектора 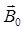 показано кружком с крестиком в центре рамки. Заметим, что при расчете магнитных полей постоянных токов, создаваемых проводниками произвольной конфигурации так же, как и при расчете электростатических полей, широко используется принцип суперпозиции. Закон Био – Савара – Лапласа сначала записывается в основной дифференциальной форме, затем подготавливается к интегрирова­нию рабочая формула и осуществляется необходимое интегрирование.