Возьмем стандартный комплект шахматных фигур. С точки зрения шахматного игрока все белые пешки в нем одинаковы. Расставляя их на шахматной доске, шахматист будет выбирать их из коробки в произвольном порядке. В начальной позиции все они будут поставлены на вторую горизонталь и шахматист не будет размышлять над вопросом, куда ему лучше поставить выбранную наугад пешку. Точно так же любая из черных ладей при расстановке фигур перед игрой может с равным успехом попасть на королевский или ферзевый фланг. Эти ладьи одинаковы.

Но представим себе другую ситуацию: этот же комплект шахмат отдан ребенку, который играет в солдатики. Для него отдельные пешки могут приобрести индивидуальность, получить имена и метки. Однако в тот момент, когда этот же мальчик начнет использовать шахматы по прямому назначению, пешки одного цвета опять станут одинаковыми.

Возьмем еще одну ситуацию: шахматные фигуры в процессе игры. Предположим, что шахматист стоит перед выбором: отдать ли противнику пешку, проникшую уже на седьмую горизонталь и грозящую вот-вот превратиться в ферзя, или пешку, мирно стоящую в начальной позиции. Ясно, что (при прочих равных условиях) первая пешка гораздо ценней и шахматист уже не считает обе свои пешки одинаковыми. Правда, в этой ситуации объектами являются не сами по себе деревянные фигурки, а "пешки в данной позиции". В позиции этюдного характера каждая пешка играет свою индивидуальную роль, и они, разумеется, не одинаковы для хорошего шахматиста.

Разница здесь того же характера, как между словом русского языка и словом в данном контексте. Например, слова "пешка" и" пешка", хотя и напечатаны разным шрифтом, одинаковы, как слова русского языка. Но в контекстах "Гроссмейстер эффектно пожертвовал пешку" и "Он был только пешкой в чужих руках" это слово имеет разные значения. Иначе говоря, слова одинаковы, а значения различаются.

Аналогично, об одинаковости людей мы можем говорить в различном смысле. С профессиональной точки зрения продавца готового платья люди, имеющие один и тот же пол, рост и размер, неразличимы. Они одинаковы в том смысле, что им нужно демонстрировать одни и те же вещи. Впрочем, хороший продавец различает покупателей по их вкусам, а хороший портной понимает, что кроме роста и размера есть индивидуальные особенности фигуры. Но для работника склада, который выдает форму (скажем, штормовые костюмы для альпинистов), существен только размер. Для профессора анатомии малосущественно, на чьем трупе он будет демонстрировать студентам устройство человеческих органов. Но уже для профессора психиатрии нет одинаковых больных.

С точки зрения инспектора по кадрам люди с тождественными анкетными данными одинаковы. Но для научного руководителя лаборатории нет одинаковых и взаимозаменимых сотрудников.

Когда мы приглашаем к себе гостей, то нам совершенно не все равно, кто придет и кого приведет с собой. С точки зрения индивидуальных человеческих взаимоотношений ни один человек не равен другому. Когда мы говорим о всеобщем равенстве людей, то понимаем под этим в действительности равенство прав перед законом, равноценность личностей, но не равенство индивидуальностей.

Рассмотрим множество животных. Мы разобьем их на следующие шесть групп: 1 – сухопутные млекопитающие, 2 – обитающие в воде, 3 – насекомые, 4 – птицы, 5 – мифические существа, 6 – пресмыкающиеся. Будем считать по определению животных, входящих в одну группу, одинаковыми. Можно вообразить ситуацию, когда одинаковые в этом смысле животные взаимозаменимы. Например, когда учителю биологии надо показать ученикам представителей разных типов.

Если мы внимательно проанализируем, что общего в употреблении слова "одинаковость" во всех приведенных примерах, то мы увидим следующее.

Во-первых, одинаковость всегда понимается как бинарное отношение на некотором множестве объектов. Во-вторых, содержание этого отношения зависит от ситуации, в которой мы рассматриваем эти объекты, или от наблюдателя, который с выбранной им точки зрения судит об одинаковости объектов. В-третьих, слово "одинаковость" попадает в один синонимический ряд со словом "взаимозаменимость".

Действительно, одинаковость белых пешек или других одноименных и одноцветных фигур состоит в том, что любая из них может заменить другую. Каким бы шрифтом мы не печатали слово в словаре, оно остается таким же словом. Кажется очень естественным предположить, что в данной ситуации взаимозаменяемы те и только те объекты, которые одним и тем же набором формальных признаков, существенных в данной ситуации.

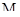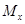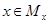Пусть  – некоторое множество объектов, в котором некоторые объекты взаимозаменимы. Обозначим через  множество всех объектов, взаимозаменимых с объектом . Очевидно, что  и объединение всех  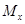(при всевозможных ) совпадает со всем множеством : .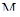

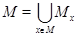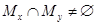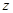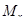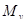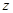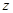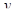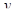Предположим, что . Это значит, что существует некоторый элемент  такой, что он одновременно принадлежит  и . Значит,  взаимозаменим с  и  взаимозаменим с . Следовательно,  взаимозаменим с , а значит и с любым элементом из 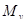. Таким образом, 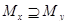. Симметричным рассуждением можно показать, что 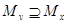. Таким образом, встречающиеся в объединении  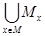множества  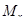либо целиком совпадают, либо не пересекаются. Проведенное выше рассуждение наводит на мысль, как можно строго определить отношение одинаковости, или взаимозаменимости. В связи с этим обратим внимание на способ употребления слов в математике. До сих пор мы имели дело со словами "одинаковость", "взаимозаменимость". Эти слова никак не определялись, а использовались так, как мы привыкли их употреблять в обыденной речи. Но с точки зрения математических понятий слово "эквивалентность" является экспликацией (точным определением) понятия одинаковости.

От сходства к толерантности

Например, две новые "Волги" одного выпуска и цвета с точки зрения покупателя вполне одинаковы и, стало быть, взаимозаменимы. Но две "Волги" разного выпуска (или новая и старая "Волги" одного выпуска) только похожи. При отсуствии необходимого выбора одна может заменить другую, если покупатель готов согласиться с подобной заменой.

Двое близнецов бывают настолько одинаковыми, что без всякого риска могут сдавать экзамены друг за друга. Если два студента только похожи, то такая жульническая проделка, хотя и осуществима, но рискована.

Если для объектов указано только сходство, то невозможно их разбить на четкие классы так, что внутри класса объекты похожи, а между объектами разных классов сходства нет. В случае сходства возникает размытая ситуация без четких границ.

Каждый элемент множества несет определенную информацию о похожих на него элементах. Но не всю информацию), как в случае одинаковых элементов. Здесь уже нет дилеммы: "Все или ничего" или "Полная информация – отсутствие информации", Здесь возможны разные степени информации, которую одни элемент содержит относительно другого.

Превосходная степень от сходства – неразличимость, а вовсе не одинаковость, как может показаться на первый взгляд. Одинаковость – свойство качественно иное. Дело в том, чю неразличимые объекты (так же, как и сходные) не разбиваются, вообще говоря, на классы так, чтобы в каждом классе элементы не различались, а элементы разных классов заведомо различались.

В самом деле. Возьмем множество точек на плоскости. Пусть величина 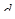 лежит ниже порога разрешимости глаза, т.е.  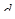– такое расстояние, при котором точки, находящиеся на этом расстоянии, неразличимы зрительно (при выбранном удалении плоскости от наблюдателя). Возьмем теперь  точек, лежащих на одной прямой и отстоящих (каждая oт соседних) на расстоянии 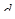. Каждая пара соседних точек неразличима, но если  достаточно велико, то первая и последняя точки будут отстоять друг от друга на метр и заведомо будут различимы. Разумеется, одинаковость есть частный случаи неразличимости и сходства.

Традиционный подход к изучению сходства или неразличимости состоит в том, чтобы сначала определить меру сходства, а затем исследовать взаимное расположение сходных объектов. Английский математик Зиман, изучая модели зрительного аппарата, предложил аксиоматическое определение сходства. Тем самым свойства сходства стало возможным изучать независимо от того, как конкретно оно задано в тон или иной ситуации: расстоянием между объектами, совпадением каких-то признаков или субъективным мнением наблюдателя.

Так же, как переход от расплывчатого понятия "одинаковость" к точно определенному тину отношении сопровождался введением пового термина "эквивалентность", математическое отношение, соответствующее нашему интуитивному представлению о сходстве или неразличимости, получило у Зимана название "толерантность". Иначе говоря, толерантность является экспликацией понятия сходства или неразличимости.

Заключение

В данной курсовой работе были рассмотрены и изучены понятия отношений эквивалентности и толерантности. В главе первой изложена информация об отношении эквивалентности: основные определения и связь между ними, свойства эквивалентности, операции над эквивалентностями, отношения эквивалентности на числовой прямой. В следующей главе содержится основной материал об отношении толерантности: основные определения и примеры толерантностей, их свойства, установлены операции над толерантностями, раскрыты понятия пространства и класса толерантности. Также установлена связь отношений эквивалентности и толерантности. В последней главе объяснены математические термины "эквивалентность" и "толерантность" с помощью таких привычных для всех слов как "одинаковость" и "сходство". С помощью этих же слов мы установили, в каких областях знаний и практики человека нашли свое применение термины "эквивалентность" и "толерантность".

Литература

1. Шрейдер Ю.А. Равенство, сходство и порядок. – М.:Наука, 1971

2. Бурбаки Н. Теория множеств. – М.:Мир, 1965

3. Общая алгебра. Т. 1./ О.В. Мельников, В.Н. Ремесленников, В.А. Роляньков и др. Под общ. ред. Л.А. Сибриянова. – М.:Наука, 1999 – 592 с.