Когда отношение толерантности оказывается транзитивным, т.е. превращается в свой частный случай – в отношение эквивалентности, то классы толерантности превращакугся в классы эквивалентности. Так как классы эквивалентности не пересекаются, справедлива

Лемма. Отношение толерантности  янлнигся отношением эквивалентности тогда и только тогда, когда классы толерантности не пересекаются друг с другом.

Вернемся теперь к изучению отображения , построенного в процессе доказательства теоремы 2.3.1 и выясним, какие элементы из 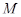 имеют одинаковый образ при отображении , т.е. отчего 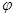 бывает не инъективным.

Определение

Пусть 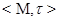 – пространство толерантности. Множество  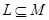называется ядром, если существует такая совокупность классов 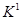, , 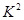, что 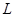 есть совокупность всех элементов из 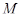, каждый из которых входит во все эти и только эти классы.

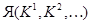Ядра – это прообразы при отображении . Действительно, ядро  состоит из всех тex элементов 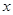, для которых образ  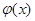есть именно это множество классов толерантности: 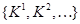. Отсюда ясно, что непустые ядра образуют разбиение, множества  и тем самым задают отношение эквивалентности. Мы попробуем разобраться, как это отношение связано с исходной толерантностью.

Пусть задано пространство толерантности 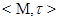, Далее мы будем обозначать через  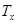множество всех элементов, толерантных к 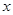. Отношение  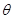на 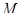 определим условием

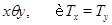
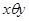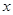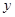Иначе говоря,  означает, что  и  толерантны к одним идем же элементам.

Лемма. Для того чтобы выполнялось соотношение , необходимо и достаточно, чтобы 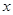 и 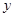 лежали в одном и том же ядре .

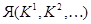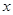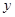Доказательство. Пусть  и  принадлежат ядру 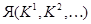. По лемме 2.3.3 множество  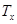состоит из всех элементов, входящих хотя бы в один из классов  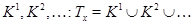Но то же самое справедливо и для множества 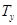, т.е.  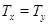или 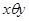. Обратно. Предположим, что 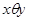, и пусть  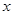принадлежит некоторому классу 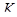. Тогда для любого  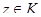будет выполнено соотношение 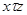. В силу выполнено и 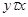. Значит,  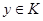(поскольку  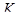– максимальный предкласс). Аналогично показывается, что всякий класс, содержащий 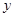, содержит одновременно 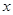. 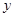Итак,  и  принадлежат одной и той же совокупности классов, а значит, и общему ядру. Лемма доказана.

Следствие. Отношение 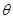 есть эквивалентность, а непустые ядра сложат для  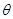классами эквивалентности.

Отметим очевидное включение

В случае эквивалентности классы не пересекаются и каждое ядро совпадает со своим классом толерантности: 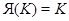, и, кроме того, для любого .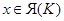

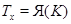Заметим, что при обобщении понятия эквивалентности – переходе к толерантности – понятие класса эквивалентности расщепляется на два разных понятия – класс толерантности и ядро.

Определение

Пространство толерантности 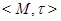 называется безъядерным, если каждое ядро состоит не более чем из одного элемента.

Для безъядерных пространств, толерантности основная классификационная теорема (тeopeмa 2.3.1) может быть уточнена так:

Теорема. Пусть 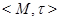 – безъядерное пространство толерантности, а  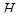– множество всех есо классов толерантности. Тогда существует инъективное отображение  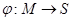такое, что элементы из  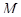толерантны в том и только том случае, когда толерантны их образы в .

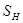Для конечных пространств с нетривиальными ядрами можно применить тот же прием, который был уже использован для задания признаками эквивалентности. А именно, выберем в каждом ядре свою нумерацию. Сопоставим каждому элементу  конечного пространства 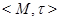 набор номеров , где 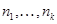 – те же самые номера, что и в 3, а  – номер элемента в своем ядре. Ясно, что элемент однозначно определяется целочисленными признаками 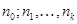, а толерантность пары определяется совпадением одного из признаков .

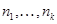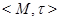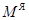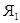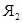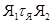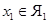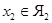Пусть теперь  – произвольное прострапсизо толерантности. Обозначим через  множество его ядер и определим толераниюсть ядер  и  условием: , если существуют представители  и , толерантные в 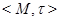. Так как элементы одного ядра имеют общее множество толерантных с ними элементов, то из 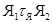, следует, что для любых  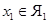и 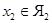 выполнено . Мы получили новое пространство 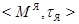. Можно убедиться, что оно будет безъядерным. 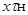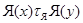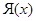Ясно Ясно также, что  равносильно , где  и 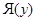 – содержащие эти элементы ядра.

Теперь заметим, что ядра можно было бы определять не с помощью полного запаса классов, а только с помощью классов, принадлежащих некоторому базису 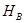. Пусть  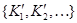– некоторая совокупность классов из базиса 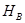. Ядром  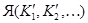относительно базиса  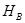мы назовем совокупность всех элементов из 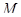, каждый из которых входит во все эти классы и не входит ни в какие другие классы из базиса .

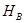Лемма. Разиение множества 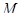 на ядра относительно базиса  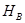совпадает с разбиением множества  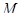на обычные ядра.

Доказательство. Буквально повторяя доказательство леммы 2.5.1, мы получим, что ядра, определенные по базису 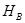 – это классы эквивалентности по 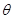. Значит, они совпадают с исходными ядрами.

Теорема. Если пространство толерантности 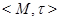 имеет конечный базис 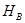, то совокупность всех классов толерантности в  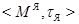конечна.

Доказательство. В силу леммы 2.5.2 число ядер конечно, т.е. конечно пространство ядер 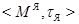. Значит,  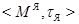имеет конечное число классов толераитпости. Но так как  равносильно 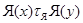, то каждый класс толерантности в  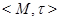есть объединение ядер, образующих соответствующий класс толерантности в 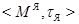. Таким образом, совокупность всех классов толерантности в  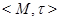конечна.

Обратим внимание, что ни в формулировке теоремы, ни в ее доказательстве не предполагается, что 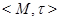 конечно. Оно и фактически может быть бесконечным за счет бесконечности ядер.