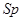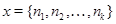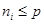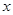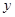Рассмотрим пространство . Это пространство толерантности состоит из множеств номеров вида , где все , причем элементы  и  толерантны, если они содержат общий номер.

Обозначим через 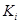 множество всех элементов, содержащих номер 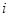. Например, пр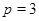и  и 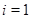,  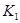состоит из элементов 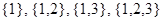. Ясно, что есл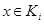и  и 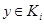, то они заведомо имеют общий номер 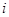, и поэтому 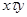. Значит,  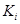есть предкласс. Пусть теперь  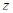– произвольный элемент, не входящий в 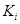, а 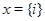 – тот элемент из 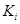, который имеет единственный номер 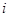. Ясно, что  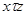не выполнено, поскольку  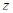не содержит номер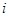а , а 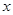 содержит только этот номер. Значит, предкласс  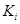нельзя расширить и поэтому справедлива следующая лемма.

Лемма

Множество 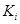 является классом толерантности.

Так как 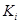 состоит из всех множеств вида 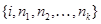, то число элементов множества  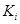равно 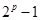 – число всех подмножеств множества из оставшихся  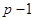номеров.

Найденных классов 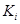 достаточно, чтобы задать толерантность в .

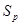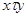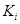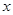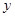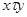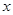Точный смысл этого утверждения состоит в том, что соотношение  выполняется тогда и только тогда, когда существует класс  содержащий одновременно  и . Действительно, если , то  и 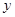 содержат некоторый общий номер 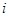, и тем самым входят в класс 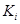. Обратное столь же очевидно. Значит, лемма 2.3.3 допускает для пространства  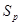уточнение. Для проверки толерантности достаточно ограничиться проверкой вхождения в один из классов 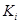. Однако, в  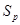кроме 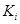 есть еще классы толерантности. Так, в  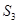множество  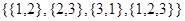образует класс. Ясно, что этот класс не совпадает ни с одним 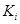, так как не содержит элементов вида .

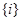Определение. Совокупность 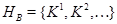 классов в пространстве толерантности  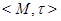называется базисом, если:

1) для всякой толерантной пары 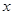 и 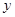 существует класс 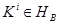, содержащий оба этих элемента: ;

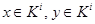2) удаление из 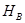 хотя бы одного класса приводит к потере этого свойства, т.е.  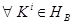существует толерантная пара 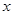, , 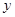для которой  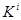является единственным общим классом толерантности в .

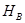Замечание. Произвольная система классов толерантности, обладающая свойством 1) из определения 2.4.1, содержит базис. Чтобы выделить этот базис, достаточно последовательно удалить "лишние" классы. В качестве исходной системы можно выбрать все множество классов. Отсюда следует существование базиса в любом пространстве толерантности.

Теорема. Пусть 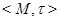 – произвольное пространство толерантности, а  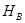– базис. Тогда существует отображение  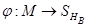такое, что элементы из  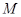толерантны в том и только в том случае, когда толерантны их образы в .

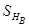Смысл теоремы состоит в том, что любое пространство толерантности реализуется как система множеств классов из базиса с естественной толерантностью типа .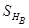

Выше было показано, что в пространстве толерантности 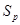 набор классов  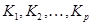образует базис, не совпадающий с совокупностью всех классов.

Установим одно простое свойство всех классов толерантности в .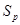

Лемма

Если 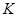 – класс толерантности в 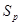, содержащий элемент 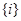, то .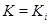

Доказательство. Действительно, все элементы, толерантные к 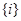, обязаны содержать номер  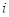в своем наборе. Значит, 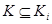. Но 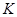 есть класс, т.е. по определению не может целиком содержаться в другом классе. Значит, .

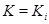Лемма

В пространстве 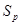 существует единственный базис: .

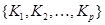Доказательство. Пусть 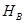 – базис в 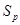. Тогда в нем должен существовать класс, содержащий элемент 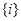. По предыдущей лемме таким классом может быть только 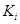. Значит, базис  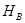должен содержать все классы 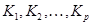. Но они уже сами образуют базис, т.е. .

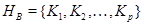В силу определения базиса толерантность в 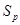 можно задать только  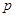признаками, соответствующими  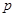базисным классам .

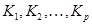Итак, в пространстве 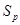 остальные классы играют чисто паразитическую роль, не участвуя ни в одном базисе. Вообще говоря, существуют пространства толерантности с неединственным базисом.

Рассмотрим пространство 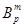. Оно состоит из целочисленных кортежей  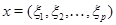длины 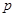, где 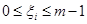. Обозначим через  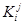множество, состоящее из всех элементов, для которых 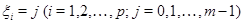. Легко проверить, что эти множества образуют классы толерантности. Итак, класс  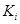– это совокупность кортежей, у которых фиксированная координата принимает фиксированное значение. Из определения толерантности в  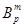сразу следует, что классы  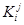образуют базис. Общее количество этих классов равно 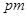, а каждый класс содержит  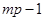элементов.