Посмотрим, какие операции над отношениями эквивалентности и при каких условиях дают в результате эквивалентность.
Транзитивное замыкание 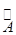 отношения эквивалентности
отношения эквивалентности  является отношением эквивалентности.
является отношением эквивалентности.
Отношение, обратное к эквивалентности, является эквивалентностью.
Если  и
и 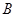 – эквивалентности, то их пересечение
– эквивалентности, то их пересечение 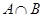 также является отношением эквивалентности.
также является отношением эквивалентности.
Сложнее обстоит дело с объединением отношений эквивалентности. Вообще говоря, объединение эквивалентностей уже не обязано быть эквивалентностью.
Действительно, отношение  дает разбиение на два класса
дает разбиение на два класса  и
и 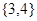 , отношению
, отношению 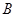 соответствует разбиение
соответствует разбиение 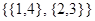 , а отношение
, а отношение 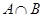 дает неполный связный граф.
дает неполный связный граф.
Теперь попробуем разобраться, когда объединение эквивалентностей дает в результате эквивалентность. Пусть 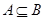 , тогда из свойств теоретикомножественных операций следует
, тогда из свойств теоретикомножественных операций следует 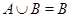 , т.е.
, т.е. 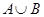 есть эквивалентность. Точно так же, если
есть эквивалентность. Точно так же, если 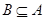 , то
, то 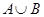 является эквивалентностью.
является эквивалентностью.
Рассмотрим более общий случай, когда множество 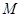 можно разбить на два непересекающихся подмножества
можно разбить на два непересекающихся подмножества 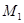 и
и  (из которых одно может быть пустым) так что
(из которых одно может быть пустым) так что
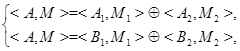
и при этом
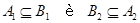
В этом случае отношения  и
и 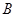 мы назовем когерентными.
мы назовем когерентными.
Легко видеть, что если 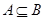 или
или  , то отношения
, то отношения  и
и  когерентны (надо положить
когерентны (надо положить 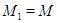 ,
, 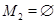 ). Таким образом, сравнимость относительно "порядка", задаваемого включением, есть частный случай когерентности.
). Таким образом, сравнимость относительно "порядка", задаваемого включением, есть частный случай когерентности.
Из следует, что для когерентных отношении эквивалентности  и
и  :
: 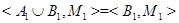 и
и 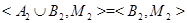 . Используя определение прямой суммы и , получаем
. Используя определение прямой суммы и , получаем  . Здесь
. Здесь  и
и 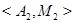 – эквивалентности (как сужения эквивалентиостей
– эквивалентности (как сужения эквивалентиостей  и
и 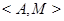 ), а
), а 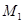 , и
, и 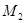 не пересекаются. По теореме 1.2.3 отсюда следует, что
не пересекаются. По теореме 1.2.3 отсюда следует, что 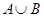 есть отношение эквивалентности.
есть отношение эквивалентности.
Оказывается, когерентность отношений  ,
, 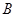 является не только достаточным, но и необходимым условием для того, чтобы объединение
является не только достаточным, но и необходимым условием для того, чтобы объединение 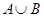 эквивалентностей
эквивалентностей  и
и 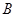 было эквивалентностью.
было эквивалентностью.
Теорема
Для того чтобы объединение 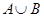 эквивалентностсй
эквивалентностсй  и
и  само было отношением эквивалентности, необходимо и достаточно, чтобы
само было отношением эквивалентности, необходимо и достаточно, чтобы  и
и  были когерентными.
были когерентными.
Нам понадобятся некоторые простые свойства разбиений на классы эквивалентности, которые мы сформулируем в виде самостоятельных лемм. Мы будем далее использовать некоторые словесные сокращения. Если  – эквивалентность и
– эквивалентность и 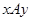 , то мы будем говорить, что
, то мы будем говорить, что 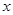 и
и 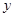
 -эквивалентны. Разбиение, соответствующее эквивалентности
-эквивалентны. Разбиение, соответствующее эквивалентности  , мы будем называть
, мы будем называть  -разбиением;
-разбиением;  -классами и т.п.
-классами и т.п.
Лемма. Для того чтобы 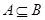 , необходимо и достаточно, чтобы каждый
, необходимо и достаточно, чтобы каждый  -класс содеожался в некотором
-класс содеожался в некотором 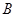 -классе.
-классе.
Действительно, если 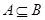 , то из
, то из 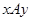 следует
следует  . Зчачит, множество всех
. Зчачит, множество всех 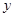 ,
,  -эквивалентных элементу
-эквивалентных элементу 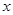 , содержится во множестве всех
, содержится во множестве всех 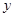 ,
,  -эквивалентных этому
-эквивалентных этому 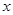 . Обратный вывод столь же очевиден.
. Обратный вывод столь же очевиден.
Для того чтобы 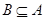 необходимо и достаточно, чтобы каждый
необходимо и достаточно, чтобы каждый  -класс
-класс  содержал любой
содержал любой 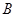 -класс
-класс 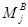 , имеющий с
, имеющий с 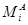 непустое пересечение.
непустое пересечение.
Для доказательства необходимости выберем произвольный элемент 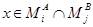 . По предыдущей лемме
. По предыдущей лемме 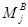 целиком содержится в некотором классе
целиком содержится в некотором классе  . Но если бы
. Но если бы 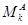 был бы отличен от
был бы отличен от  , то элемент
, то элемент 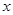 был бы сразу в двух классах
был бы сразу в двух классах  -разбиения, что невозможно. Значит,
-разбиения, что невозможно. Значит, 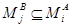 . Для доказательства достаточности нужно только вспомнить, что из
. Для доказательства достаточности нужно только вспомнить, что из 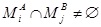 по условию вытекает
по условию вытекает 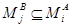 , и применить лемму 1.3.1.
, и применить лемму 1.3.1.
Для того чтобы эквивалентности  и
и 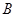 были когерентными, необходимо и достаточно, чтобы всякий
были когерентными, необходимо и достаточно, чтобы всякий  -класс
-класс 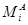 либо содержался в некотором
либо содержался в некотором  -классе
-классе  , либо целиком содержал любой
, либо целиком содержал любой 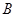 -класс
-класс 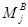 , имеющий с
, имеющий с 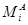 непустое пересечение.
непустое пересечение.
Доказательство. Eсли  и
и 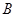 когерентны, то
когерентны, то 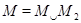 ,
, 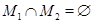 и на
и на 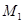 , имеем
, имеем 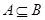 , а на
, а на 
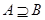 . Тогда по лемме 1.3.1 для каждого класса
. Тогда по лемме 1.3.1 для каждого класса  , содержащегося в
, содержащегося в 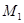 , существует такой класс
, существует такой класс 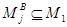 , что
, что  . По лемме 1.3.2 каждый класс
. По лемме 1.3.2 каждый класс 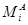 , содержащийся в
, содержащийся в  , целиком содержит любой класс
, целиком содержит любой класс 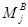 , имеющий с
, имеющий с  непустое пересечение. Поскольку
непустое пересечение. Поскольку 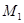 и
и  не пересекаются, из вытекает, что всякий класс эквивалентности
не пересекаются, из вытекает, что всякий класс эквивалентности  содержится либо в
содержится либо в 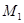 , либо в
, либо в 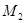 ; значит, наше рассуждение охватывает все классы.
; значит, наше рассуждение охватывает все классы.
Проведем доказательство в обратную сторону. Пусть каждый класс  обладает сформулированным в лемме 1.2.3 свойством. Обозначим через
обладает сформулированным в лемме 1.2.3 свойством. Обозначим через 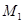 объединение всех тех классов
объединение всех тех классов 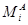 , для которых существует такой
, для которых существует такой 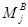 , что
, что 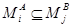 , а через
, а через  – объединение остальных классов
– объединение остальных классов  . Ясно, что
. Ясно, что 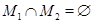 ,
, 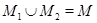 и
и 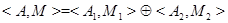 ,
, 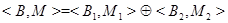 , где
, где 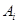 и
и  – сужения отношений
– сужения отношений  и
и 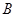 на
на  . Наконец, очевидно, что
. Наконец, очевидно, что 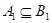 и
и  , т.е.
, т.е.  и
и  когерентны.
когерентны.
Теперь мы подготовили все необходимое для доказательства теоремы 1.3.1. Будем вести доказательство от противного, т.е. предположим, что  и
и  не когерентны. Тогда по лемме 1.3.3 существует класс
не когерентны. Тогда по лемме 1.3.3 существует класс 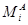 и класс
и класс 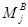 такиее, что
такиее, что  , но не один из них не содержит другой. Значит, существуетвует
, но не один из них не содержит другой. Значит, существуетвует 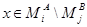 , существует
, существует 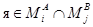 , существует
, существует 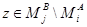 . Имеем следующие соотношения:
. Имеем следующие соотношения: 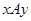 и
и 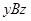 , следовательно,
, следовательно, 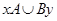 и
и  . По транзитивности должно было бы быть также
. По транзитивности должно было бы быть также 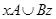 . Однако, соотношения:
. Однако, соотношения:  и
и  – оба не выполнены, так как
– оба не выполнены, так как 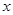 не лежит с
не лежит с  ни в общем
ни в общем  -классе, ни в общем
-классе, ни в общем 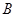 -классе. Значит, соотношение
-классе. Значит, соотношение 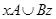 не выполнено. Полученное противоречие доказывает теорему.
не выполнено. Полученное противоречие доказывает теорему.
Замечание. Понятие когерентности имеет смысл для любых отношений  и
и  . Но для эквивалентностей когерентность отношений
. Но для эквивалентностей когерентность отношений  и
и  легко формулируется в терминах классов эквивалентности (лемма 1.3.3).
легко формулируется в терминах классов эквивалентности (лемма 1.3.3).
Лемма
Если  и
и 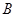 рефлексивны, то
рефлексивны, то
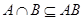
Доказательство. Если 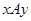 , то, в силу
, то, в силу 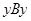 , выполнено и соотношение
, выполнено и соотношение  , т.е.
, т.е. 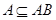 . Аналогично получается
. Аналогично получается 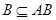 . Из этих двух включений следует .
. Из этих двух включений следует .
Теорема. Для того чтобы объединение 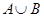 эквивалентностей
эквивалентностей  и
и  само было отношением эквивалентности, необходимо и достаточно, чтобы
само было отношением эквивалентности, необходимо и достаточно, чтобы
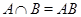
Доказательство. Пусть 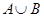 – эквивалентность. По лемме 1.3.4 выполняется . Для доказательства остается доказать
– эквивалентность. По лемме 1.3.4 выполняется . Для доказательства остается доказать
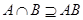
Пусть 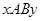 . Тогда для некоторого
. Тогда для некоторого  имеем
имеем  и
и 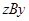 . Следовательно,
. Следовательно,  и
и  . Значит,
. Значит,  и доказано. Пусть теперь выполнено . Отношение
и доказано. Пусть теперь выполнено . Отношение 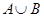 симметрично. По тогда симметрично и ортношение
симметрично. По тогда симметрично и ортношение  .
. 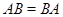 . По теореме 1.3.3 (см. ниже) получаем, что отношение
. По теореме 1.3.3 (см. ниже) получаем, что отношение  – эквивалентность. Из вытекает, что и
– эквивалентность. Из вытекает, что и 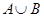 – эквивалентность. Теорема доказана.
– эквивалентность. Теорема доказана.
Условие, при котором произведение  двух отношений эквивалентности
двух отношений эквивалентности  и
и 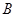 само является эквивалентностью, было получено чешским математиком Шиком в 1954 г.
само является эквивалентностью, было получено чешским математиком Шиком в 1954 г.
Для того чтобы произведение  отношений эквивалентности
отношений эквивалентности  и
и  было эквивалентностью, необходимо и достаточно, чтобы
было эквивалентностью, необходимо и достаточно, чтобы  и
и  коммутировали.
коммутировали.
Доказательство. Пусть сначала
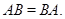
 рефлексивно.
рефлексивно.  симметрично. Транзитивность произведения доказывается так:
симметрично. Транзитивность произведения доказывается так: 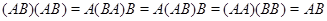 – здесь мы использовали ассоциативный закон для произведения отношений, условие , а также транзитивность и рефлексивность отношений
– здесь мы использовали ассоциативный закон для произведения отношений, условие , а также транзитивность и рефлексивность отношений  и
и 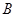 . Итак
. Итак  , но это и означает транзитивность отношения
, но это и означает транзитивность отношения  , поскольку
, поскольку  рефлексивно. Пусть теперь произведение
рефлексивно. Пусть теперь произведение  есть эквивалентность. Тогда
есть эквивалентность. Тогда 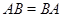 .
.
Легко проверить, что если  и
и 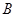 – эквивалентности, то
– эквивалентности, то 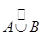 и
и  также будут эквивалентностями.
также будут эквивалентностями.
Оказывается, операция 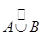 (ее иногда называют, объединением эквивалентностей, имея в виду, что обычное объединение эквивалентностей может не быть эквивалентностью) ассоциативна, т.е. является "хорошей" алгебраической операцией.
(ее иногда называют, объединением эквивалентностей, имея в виду, что обычное объединение эквивалентностей может не быть эквивалентностью) ассоциативна, т.е. является "хорошей" алгебраической операцией.
Для любых транзитивных отношений  ,
, 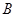 и
и  справедлив ассоциативный закон:
справедлив ассоциативный закон:

Докажем сначала две леммы.
Лемма
Для любых отношений 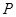 ,
, 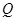


вытекает из 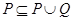 . доказывается аналогично.
. доказывается аналогично.
Лемма
Для любых транзитивных отношений 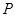 ,
, 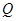 ,
, 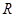 из
из 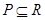 и
и 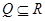 вытекает
вытекает 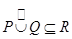 .
.
Доказательство теоремы 1.3.4. Из леммы 1.3.5


Из и
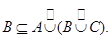
Из леммы 1.3.5
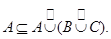
Из , , леммы 1.3.5 и того, что любое отношение вида  транзитивно,
транзитивно,
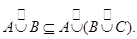
Подобно тому как доказывается , доказывается

Подобно тому как мы из и вывели , из и выводится
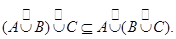
Из и аналогично доказываемого "обратного" включения вытекает . Теорема доказана.
Нетрудно убедиться, что для любой эквивалентности 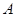

где 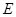 – диагональное отношение.
– диагональное отношение.
Покажем теперь, что операция 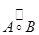 не дает ничего нового:
не дает ничего нового:
Если  и
и 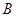 – эквивалентности, то
– эквивалентности, то

Доказательство. Заметим сначала, что, учитывая лемму 1.3.4, 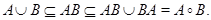 Применяя транзитивное замыкание к обеим частям, ввиду свойства монотонности транзитивного замыкания имеем
Применяя транзитивное замыкание к обеим частям, ввиду свойства монотонности транзитивного замыкания имеем

Далее, применяя распределительный закон получим
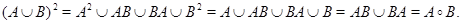
Мы использовали здесь тот факт, что для рефлексивного 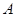 выполнено включение
выполнено включение  , а следовательно,
, а следовательно,  . Запишем теперь выражение для транзитивного замыкания, используя :
. Запишем теперь выражение для транзитивного замыкания, используя :
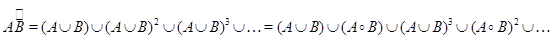
Отсюда ясно, что  , т.е.
, т.е.

Сравнивая включения и получим искомое соотношение .
Отсюда вытекает следующий результат, также принадлежащий Шику:
Теорема
Если  и
и 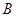 – эквивалентности и
– эквивалентности и 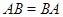 , то
, то

В самом деле, по теореме 1.3.3 произведение  является эквивалентностью, а стало быть отношение
является эквивалентностью, а стало быть отношение 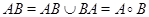 совпадает со своим транзитивным замыканием
совпадает со своим транзитивным замыканием  . Но тогда из теоремы 1.3.5 следует .
. Но тогда из теоремы 1.3.5 следует .
Дата: 2019-07-30, просмотров: 311.