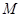Пусть задано отношение  на множестве . В случае, когда  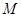– числовая прямая, отношение  отождествляется с некоторым подмножеством числовой плоскости, т.е. прямого произведения 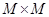. В этом параграфе будут рассмотрены геометрические свойства множества  на плоскости в случае, когда отношение 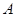 есть эквивалентность.

Согласно определению 1.2.1 отношение  называется эквивалентностью, если оно рефлексивно, симметрично и транзитивно. Каждое из этих свойств порождает некоторое геометрическое свойство множества . Координаты точки на плоскости будем обозначать .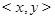

1. Рефлексивность. Из того, что 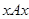 для всех 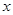, следует, что множество  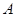содержит главную диагональ (свойство ).

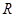2. Симметричность. Симметричность означает, что если 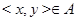, то и 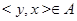, т.е. что множество  симметрично относительно главной диагонали (свойство ).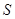

3. Транзитивность. Транзитивность означает, что есл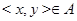и  и 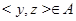, то и 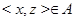. Точка  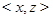является четвертой вершиной прямоугольника, три вершины которого находятся в точках  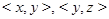и 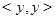. Заметим, что вершина  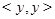лежит на биссектрисе координатного угла – главной диагонали координатной плоскости. Поэтому геометрически свойство транзитивности можно сформулировать следующим образом:

Множество  на плоскости определяет транзитивное отношение тогда и только тогда, когда для любого прямоугольника, одна вершина которого  лежит на главной диагонали, а две соседние с 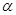 вершины принадлежат 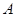, вершина 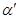, противоположная 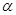, также принадлежит  (свойство ).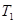

Замечание. Если отношение  является симметричным, то геометрическая формулировка транзитивности несколько упрощается. А именно:

Множество  на плоскости, симметричное относительно главной диагонали, определяет транзитивное отношение тогда и только тогда, когда для любого прямоугольника, одна вершина которого лежит на главной диагонали, а две другие принадлежат , четвертая вершина также принадлежит 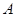 (свойство ).

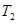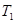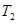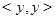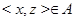Разница с предыдущим утверждением состоит в том, что вершины, принадлежащие , не обязаны быть соседними с вершиной, лежащей на диагонали. Покажем, что для симметричного  свойство , влечет . Пусть, например, вершина, лежащая на диагонали, имеет координаты  и  и 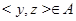; покажем, что 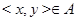. В самом деле, в силу симметрии, вместе с  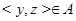имеем 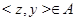. Если в качестве вершины на диагонали взять теперь 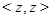, а в качестве соседних с ней вершин, принадлежащих ,  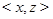и 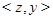, то, в силу свойства  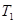получаем .

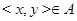Заметим, что класс эквивалентности, содержащий точку 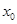, есть проекция пересечения множества  и прямой 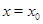 на ось ординат.

Сейчас мы приведем некоторые примеры множеств на плоскости, определяющих отношение эквивалентности.

1 Пример. (тривиальный). Множество  вся плоскость. Выполнение свойств 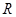, , 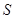 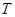очевидно. Все точки исходной прямой  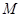отождествляются, т.е. входят в один класс эквивалентности.

Замечание. Для любого 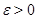, если множество , определяющее отношение эквивалентности, содержит полосу 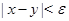, то оно совпадает со всей плоскостью. В самом деле, вместе с любой точкой  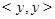множество  содержит все внутренние точки квадрата с вершинами , , 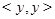, , 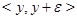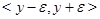т.е. полосу 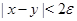. Ясно, что таким образом свойство "принадлежать 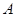" распространяется на все точки плоскости.

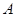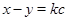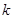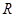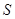2 Пример. (периодичность). Возьмем которое число. Пусть множество  состоит из прямых , где  – произвольное целое число. Выполнение свойств  и  очевидно, и если 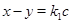, , 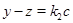то .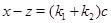

3 Пример. "Все константы равны единице, кроме нуля". (Такое утверждение высказал И.М. Гельфанд на одной из своих лекций.) В этом примере множество 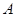 есть вся плоскость с выброшенными осями координат и добавленным началом координат. Иначе говоря,  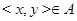всегда, кроме случая 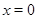,  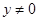и ему симметричного. Если точки ,  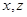принадлежат , то либо 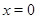, и тогда 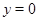, , либо , и тогда  и 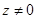. В обоих случаях .

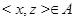4 Пример. (Все целые числа равны друг другу.) Множество 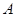 состоит из главной диагонали и всех точек с целыми координатами.

Очевидно, можно рассматривать и конечные варианты такой эквивалентности типа

5 Пример. (Все числа, не большие единицы по модулю, равны друг другу.) Множество  состоит из диагонали и замкнутого единичного квадрата. Очевидно, множество, состоящее из открытого (или полузамкнутого: 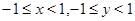) квадрата, также дает эквивалентность.

Отношение толерантности

2.1 Определения, примеры, свойства

Определение

Отношение  на множестве  называется толерантностью или отношением толерантности, если оно рефлексивно и симметрично.

Пример. Множество 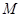 состоит из четырехбуквенных русских слов – нарицательных существительных в именительном падеже. Будем называть такие слова сходными, если они отличаются не более чем на одну букву. Известная задача "Превращение мухи в слона" в точных терминах формулируется так:

Найти такую последовательность слов, начинающуюся словом "муха" и кончающуюся словом "слон", любые два соседних слова в которой сходны (в смысле только что данного определения).

Приведем решение этой задачи: Муха – мура – тура – тара – кара – каре – кафе – кафр – каюр – каюк – крюк – крок – срок – сток – стон – слон.

Пример

Пусть 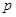 – натуральное число. Обозначим через  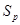– совокупность всех непустых подмножеств множества 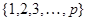. Два таких подмножества объявим толерантными, если у них есть хотя бы один общий элемент. Законность такого определения очевидна: рефлексивность и симметричность отношения легко проверяются.

Множество 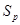 называется 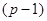-мерным симплексом. Это понятие обобщает понятия отрезка, треугольника и тетраэдра на многомерный случай. Числа  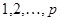интерпретируются как вершины симплекса. Двухэлементные подмножества – как ребра, трехэлементные как плоские грани, -элементные подмножества – как 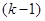-мерные грани. Толерантность граней симплекса  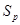означает их геометрическую инцидентность – наличие общих вершин. Число всех элементов из  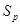равно .

Множество  с заданным на нем отношением толерантности 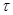 называется пространством толерантности. Таким образом, пространство толерантности есть пара .

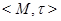Пример

Пусть 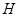 – произвольное множество. Обозначим через  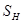совокупность всех непустых подмножеств множества 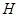. Толерантность  на 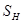 задается условием: , если .

Пространство 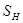 играет роль "универсального" пространства толерантности.

Пример

Возьмем произвольное множество 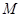 (для наглядности можно представить отрезок на прямой). Пространство толерантности  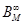состоит из всех числовых функций, определенных на этом множестве, т.е. функций, которые каждому элементу из  сопоставляют некоторое число. Две функции будут толерантными, если хотя бы на одном элементе из 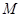 эти функции принимают одно и тоже значение (если, другими словами, графики этих функций пересекаются).

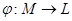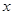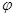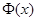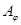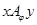Существует еще один способ задания отношений толерантности. Рассмотрим соответствие . Множество всех образов элемента  при соответствии  мы обозначим . Отношение  на множестве  задается условием: , если у элементов  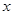и 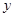 существует образ, т.е. если .

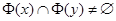Установим основные свойства отношения :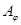

Отношение 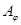 всегда симметрично.

Это следует из того, что .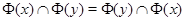

Отношение 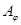 рефлексивно тогда и только тогда, когда соответствие  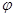определено на всем .

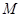В самом деле, в этом и только в этом случае множество .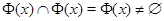

Если на элементе 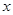 отношение  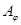не рефлексивно (не выполняется  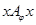или 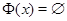), то соотношение  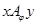не выполнено ни для какого 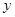, так как .

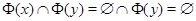Если соответствие  является функцией, т.е.  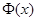состоит не более чем из одного элемента (в этом случае  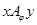равносильно 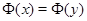), то отношение  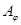транзитивно.

Действительно, пусть  и 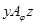. Это значит, что  и 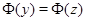. Следовательно, 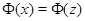, т.е. .

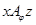Из свойств следует, что всюду определенное соответствие  определяет на 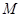 симметричное и рефлексивное отношение 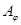, т.е. толерантность.