Рассмотрим множество 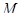 и его покрытие
и его покрытие 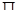 . Пару
. Пару 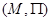 мы будем далее называть картой.
мы будем далее называть картой.
Произвольная карта 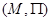 позволяет ввести на множестве
позволяет ввести на множестве 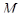 отношение толерантности
отношение толерантности 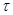 , определенное условием:
, определенное условием:  , если существует такое
, если существует такое 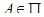 , что одновременно
, что одновременно 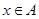 и
и 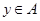 . Так определенную толерантность
. Так определенную толерантность 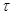 мы назовем толерантностью, порожденную картон
мы назовем толерантностью, порожденную картон 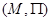 . Очевидно, каждое
. Очевидно, каждое 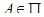 является предклассом порожденной толерантности
является предклассом порожденной толерантности 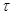 .
.
Если 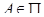 – пространство толерантности и
– пространство толерантности и 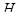 – множество всех классов толерантности в этом пространстве, то, в силу леммы 2.3.3 толерантность, порожденная картой
– множество всех классов толерантности в этом пространстве, то, в силу леммы 2.3.3 толерантность, порожденная картой 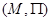 , совпадает с исходной толерантностью
, совпадает с исходной толерантностью 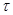 . Аналогичное утверждение справедливо и для произвольного базиса
. Аналогичное утверждение справедливо и для произвольного базиса 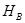 в пространстве
в пространстве 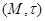 .
.
Карта 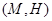 называется канонической, если каждый элемент
называется канонической, если каждый элемент 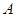 покрытия
покрытия 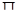 оказывается классом толерантности, порожденной исходной картон
оказывается классом толерантности, порожденной исходной картон 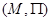 . Легко видеть, что если карта
. Легко видеть, что если карта 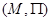 является канонической, то
является канонической, то 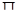 содержит некоторый базис
содержит некоторый базис 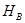 , порожденный толерантности:
, порожденный толерантности: 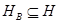 .
.
На рис. 1 изображена некоторая карта 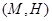 , а справа система классов порожденной толерантности (впрочем, в данном случае эта система состоит из одного класса). Этот пример показывает, в частности, существование неканонических карт.
, а справа система классов порожденной толерантности (впрочем, в данном случае эта система состоит из одного класса). Этот пример показывает, в частности, существование неканонических карт.
Каждая карта 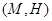 естественным образом приводит к всюду определенному соответствию
естественным образом приводит к всюду определенному соответствию

которое каждому элементу 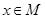 сопоставляет все те
сопоставляет все те 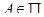 , для которых
, для которых 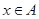 . Наоборот, если дано некоторое всюду определенное соответствие
. Наоборот, если дано некоторое всюду определенное соответствие 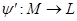 , то оно порождает покрытие
, то оно порождает покрытие  множества
множества 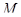 , состоящее из прообразов элементов из
, состоящее из прообразов элементов из 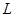 при соответствии
при соответствии  . Таким образом,
. Таким образом, 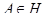 тогда и только тогда, когда существует такое
тогда и только тогда, когда существует такое 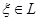 , что
, что 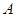 есть множество элементов из
есть множество элементов из 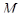 , которым соответствие
, которым соответствие 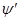 сопоставляет
сопоставляет 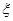 . Обозначим для дальнейшего прообраз элемента
. Обозначим для дальнейшего прообраз элемента 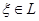 при соответствии
при соответствии 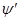 через
через 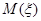 .
.
По соответствию можно построить отображение,

которое каждому элементу 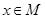 сопоставляет непустое множество элементов
сопоставляет непустое множество элементов  , для которых
, для которых 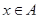 . С помощью отображении толерантность
. С помощью отображении толерантность 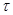 , порожденная исходной картой
, порожденная исходной картой 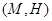 , выражается условием
, выражается условием  , если
, если 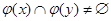 . Можно ввести еще и отношение
. Можно ввести еще и отношение 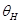 , определяемое условием:
, определяемое условием: 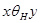 , если
, если 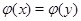 .
. 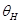 , очевидно, является эквивалентностью.
, очевидно, является эквивалентностью.
Посмотрим на примерах, как канонические признаки выражаются через исходные признаки карты. В примере на рис. 1 Имеем 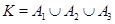 .
.
В примере на рис. 2а, изображено соответствие: 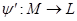 , где
, где  ,
, 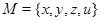 . Нa рис. 2б изображены классы порожденной толерантности. Легко проверить, что
. Нa рис. 2б изображены классы порожденной толерантности. Легко проверить, что  ,
, 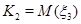 .
.
На рис 3 исходная карта уже является канонической. Но если взять каноническую карту 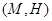 с полным набором классов толерантности, то получим, что
с полным набором классов толерантности, то получим, что 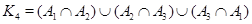 . Посмотрим далее, каким образом и всегда ли канонические признаки могут быть выражены через исходные.
. Посмотрим далее, каким образом и всегда ли канонические признаки могут быть выражены через исходные.
Теорема
Для произвольной карты 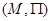 любой класс порожденной толерантности
любой класс порожденной толерантности 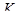 всегда может быть выражен через элементы покрытия
всегда может быть выражен через элементы покрытия 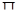 с помощью операций пересечения и объединения.
с помощью операций пересечения и объединения.
Доказательство. Рассмотрим некоторый класс толерантности 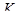 . Пусть
. Пусть 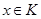 . По определению класса, для всякого
. По определению класса, для всякого 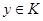 ,
, 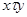 , а по определению толераптности существует признак
, а по определению толераптности существует признак 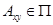 такой, что
такой, что 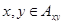 . Тогда 1)
. Тогда 1) 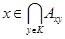 ; 2)
; 2) 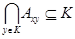 . Действительно, 1) следует из того, что
. Действительно, 1) следует из того, что 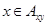 для всех признаков
для всех признаков 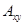 , a 2) следует из того, что всякий
, a 2) следует из того, что всякий  , принадленжащий
, принадленжащий 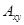 , толерантен к
, толерантен к  . Поскольку
. Поскольку 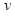 – произвольный элемент из
– произвольный элемент из 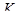 , по свойству максимальности класса
, по свойству максимальности класса 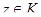 . Отсюда вытекает, что
. Отсюда вытекает, что 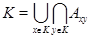 , что доказывает теорему.
, что доказывает теорему.
Подчеркнем, что канонические признаки оправляются через исходные без перехода к дополнениям. О связи между исходными и каноническими признаками говорит также.
Теорема
Существует такой базис классов порожденной толерантности, что каждый из классов этого базиса содержит некоторое множество 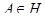 .
.
Доказательство. По определению толерантности в 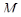 для всякого
для всякого  любая пара
любая пара 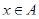 и
и 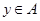 толерантна. Значит,
толерантна. Значит, 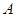 есть предкласс. Тогда по лемме 2.3.2 получается существует класс
есть предкласс. Тогда по лемме 2.3.2 получается существует класс 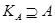 . Выберем для каждого
. Выберем для каждого 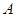 один из классов
один из классов 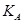 . Очевидно, выбранная совокупность классов удовлетворяет условию 1) из определения 1.4.1. Значит, она содержит некоторый базис
. Очевидно, выбранная совокупность классов удовлетворяет условию 1) из определения 1.4.1. Значит, она содержит некоторый базис 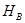 .
.
Следствие. Когда 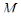 конечно, то существует базис классов толерантности, число классов в котором не превышает количества исходных признаков.
конечно, то существует базис классов толерантности, число классов в котором не превышает количества исходных признаков.
Рассмотрим исходную карту 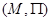 и полученную из нее каноническую карту
и полученную из нее каноническую карту 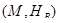 , где
, где 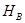 – базис. Как уже было отмечено, отношения толерантности, издаваемые на множестве обьектов
– базис. Как уже было отмечено, отношения толерантности, издаваемые на множестве обьектов 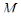 обеими картами, совпадают.
обеими картами, совпадают.
Несколько иначе обстоит дело с отношением эквивалентности 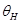 , задаваемым на
, задаваемым на 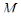 с помощью определения, приведенного в начале параграфа. Пусть
с помощью определения, приведенного в начале параграфа. Пусть 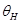 – отношение эквивалентности, заданное исходным множеством признаков
– отношение эквивалентности, заданное исходным множеством признаков 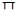 , а
, а 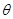 – отношение эквивалентности, заданное по . Как показывает пример на рис. 1, отношения
– отношение эквивалентности, заданное по . Как показывает пример на рис. 1, отношения 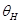 и
и 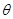 могут и не совпадать. В общем, случае справедлива
могут и не совпадать. В общем, случае справедлива
Теорема
Если выполнено соотношение: 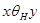 , то выполнено и соотношение
, то выполнено и соотношение 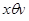 , т.е.
, т.е. 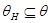 .
.
Доказательство. Если 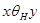 , то совокупности исходных признаков
, то совокупности исходных признаков 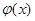 и
и 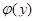 , выполненных для
, выполненных для 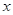 и
и  , совпадают. Из теоремы 2.6.1 вытекает, что для каждого класса толерантности
, совпадают. Из теоремы 2.6.1 вытекает, что для каждого класса толерантности 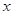 и
и  одновременно содержатся или не содержатся в нем. Таким образом,
одновременно содержатся или не содержатся в нем. Таким образом, 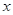 и
и 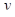 имеют одинаковые наборы канонических признаков, т.е.
имеют одинаковые наборы канонических признаков, т.е. 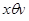 . Теорема доказана.
. Теорема доказана.
Следующая теорема, принадлежащая С.М. Якубович, дает условия того, что некоторое множество является классом толерантности, т.е. того, что некоторый признак является каноническим.
Теорема
Пусть имеется карта 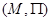 . Для, того чтобы элемент покрытия
. Для, того чтобы элемент покрытия 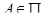 являлся классом порожденной толерантности
являлся классом порожденной толерантности 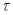 , необходимо и достаточно, чтобы для любого подмножества
, необходимо и достаточно, чтобы для любого подмножества 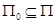 , из
, из 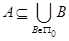 следоаало бы
следоаало бы  .
.
Доказательство. Сначала предположим, что множество 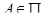 не является классом толерантности. Так как
не является классом толерантности. Так как 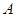 является предклассом, то единственная причина, по которой
является предклассом, то единственная причина, по которой 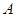 может не быть классом, состоит в том, что существует
может не быть классом, состоит в том, что существует 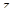 , не входящий в
, не входящий в 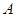 и толерантный ко всем элементам
и толерантный ко всем элементам 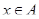 . Значит, для всякого
. Значит, для всякого 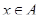 существует множество
существует множество 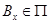 , содержащее
, содержащее 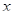 и
и 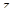 . Таким образом, множества
. Таким образом, множества 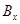 образуют покрытие множества
образуют покрытие множества 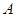 . Но все
. Но все 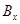 содержат элемент
содержат элемент 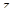 , не входящий в
, не входящий в 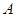 . Следовательно, пересечение
. Следовательно, пересечение 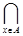 не содержится в
не содержится в 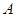 . Итак, мы доказали достаточность условия, указанною в теореме 2.6.4. Докажем теперь необходимость. Пусть существует такое подмножество
. Итак, мы доказали достаточность условия, указанною в теореме 2.6.4. Докажем теперь необходимость. Пусть существует такое подмножество 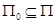 , что
, что 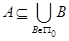 , но
, но 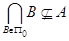 . Значит, существует элемент
. Значит, существует элемент  , не входящий в
, не входящий в 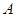 , но входящий во все
, но входящий во все 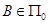 . Этот элемент толерантен ко всем
. Этот элемент толерантен ко всем 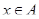 . Значит,
. Значит, 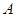 не является максимальным предклассом, т.е. не является классом толерантности. Теорема доказана.
не является максимальным предклассом, т.е. не является классом толерантности. Теорема доказана.
Рассмотрим еще так называемые сопряженные и производные пространства толерантности.
Пусть 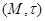 – произвольное пространство толерантности, и пусть
– произвольное пространство толерантности, и пусть  – некоторая совокупность классов толерантности. Множество
– некоторая совокупность классов толерантности. Множество  естественным образом превращается в пространство толерантности
естественным образом превращается в пространство толерантности 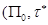 при помощи следующего определения:
при помощи следующего определения: 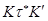 , если
, если 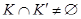 .
.
Определение. Если  совпадает с множеством
совпадает с множеством 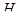 всех классов, то пространство
всех классов, то пространство 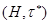 называется сопряженным к
называется сопряженным к 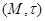 и обозначается
и обозначается 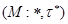 (таким образом,
(таким образом, 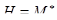 ).
).
Рассмотрим несколько примеров.
В пространстве  элемент
элемент 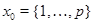 , содержащий все числа, толерантен ко всем элементам и, стало быть, входит во все классы толерантности. Значит, в пространствe
, содержащий все числа, толерантен ко всем элементам и, стало быть, входит во все классы толерантности. Значит, в пространствe 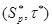
 – полное отношение.
– полное отношение.
На рис. 4 изображен циклический граф из 7 вершин. Классами толерантности являются "ребра", а толерантны классы, соответствующие смежным ребрам. Ясно, что для линейного графа из  вершин сопряженным является линейный граф из
вершин сопряженным является линейный граф из 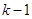 вершин.
вершин.
На рис. 5 изображен циклический граф. Сопряженным к нему будет циклический граф из того же числа верин (если количество вершин исходного графа было больше трех).
На рис. 6 изображено пространство толерантности 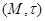 , состоящее из двух циклов, зацепленных в одной точке. Сопряженное пространство
, состоящее из двух циклов, зацепленных в одной точке. Сопряженное пространство 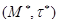 состоит из таких же циклов с более сложным зацеплением. Но сопряженное к последнему пространство
состоит из таких же циклов с более сложным зацеплением. Но сопряженное к последнему пространство 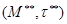 по существу совпадает с исходным пространством
по существу совпадает с исходным пространством 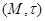 .
.
Определение. Пусть 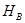 – базис. Тогда пространство
– базис. Тогда пространство 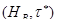 называется сопряженным к
называется сопряженным к 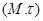 , относительно данного базиса
, относительно данного базиса 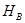 .
.
Определение. Второе сопряженное пространство относительно некоторого базиса 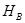 в
в 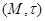 и базиса
и базиса 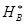 в
в 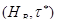 называется производным от исходного пространства толерантности
называется производным от исходного пространства толерантности 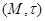 .
.
Итак, производное пространство толерантности определяется не однозначно, а с точностью до выбора базисов. Этот произвол исключается, когда 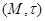 и
и 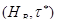 имеют по единственному базису.
имеют по единственному базису.
Рассмотрим несколько примеров.
1. Для линейного графа с  вершинами
вершинами 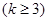 производное пространство также есть линейный граф, но с
производное пространство также есть линейный граф, но с 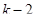 вершинами (см. рис. 4)
вершинами (см. рис. 4)
2. Для циклического графа с  вершинами
вершинами 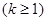 производное пространство "совпадает" с исходным пространством (см. рис. 5).
производное пространство "совпадает" с исходным пространством (см. рис. 5).
3. Та же ситуация для зацепленных циклических графов (см. рис. 6).
4. Для пространства  производное пространство
производное пространство 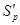 состоит из одного элемента.
состоит из одного элемента.
Теорема
Если 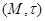 – произвольное пространство толерантности, а
– произвольное пространство толерантности, а 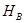 – произвольный базис в нем, то существует такой базис
– произвольный базис в нем, то существует такой базис 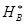 в сопряженном пространстве
в сопряженном пространстве 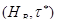 и такое инъективное отображение
и такое инъективное отображение 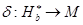 , что при
, что при 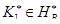 и
и 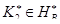 из
из 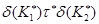 следует
следует 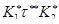 .
.
Доказательство. Обозначим через 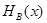 множество классов из базиса
множество классов из базиса 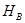 , содержащих
, содержащих  . Для любых классов
. Для любых классов 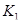 и
и  из
из 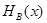 имеем
имеем 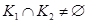 , т.е.
, т.е. 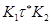 . Итак, множества
. Итак, множества 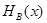 суть предклассы в
суть предклассы в 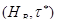 . Значит, для всякого
. Значит, для всякого 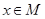 существует класс в
существует класс в 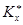 , для которого
, для которого 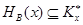 . Зафиксируем для каждого
. Зафиксируем для каждого 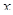 некоторый класс
некоторый класс 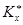 и множество этих классов обозначим через
и множество этих классов обозначим через  . Мы имеем сюръекцию
. Мы имеем сюръекцию 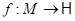 , которое каждому
, которое каждому 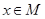 сопоставляет класс
сопоставляет класс 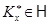 . Покажем, что
. Покажем, что  содержит некоторый базис
содержит некоторый базис 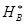 . Действительно, если
. Действительно, если 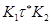 , то существует
, то существует 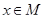 , содержащийся в
, содержащийся в 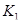 и
и  . Тогда
. Тогда 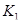 и
и  содержаться в
содержаться в 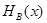 , а значит,
, а значит,  и
и 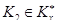 . Теперь для каждого
. Теперь для каждого 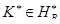 выберем ровно один элемент
выберем ровно один элемент 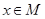 , для которого
, для которого  . Множество таких элементов обозначим через
. Множество таких элементов обозначим через  . Ясно, что
. Ясно, что 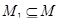 и возникающая при этом сюръекция
и возникающая при этом сюръекция  на
на 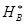 инъективно. Тогда обратное к нему отображение
инъективно. Тогда обратное к нему отображение 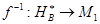 инъективно отображает
инъективно отображает 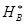 на подмножество
на подмножество  множества
множества 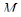 . Поэтому его можно рассматривать как инъективное (но уже в общем случае не сюръективное) отображение. Пусть теперь
. Поэтому его можно рассматривать как инъективное (но уже в общем случае не сюръективное) отображение. Пусть теперь 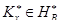 и,
и, 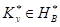 где
где 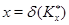 и
и 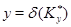 и
и 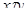 . Тогда существует класс
. Тогда существует класс 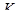 , содержащий
, содержащий 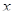 и
и 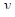 . Значит,
. Значит, 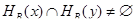 . Но из
. Но из 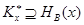 и
и  следует, что
следует, что 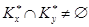 , т.е.
, т.е. 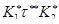 . Теорема доказана.
. Теорема доказана.
Приложение понятий эквивалентности и толерантности в различных областях знаний и практики человека
Дата: 2019-07-30, просмотров: 279.