Алгебраические свойства операций над толерантностями сравнительно просты.
Лемма
Если  – толерантность,
– толерантность, 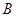 – эквивалентность и
– эквивалентность и 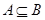 , то
, то 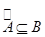 .
.
Доказательство получается применением транзитивного замыкания к обеим частям включения 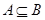 .
.
Смысл этой леммы в том, что транзитивное замыкание  отношения толерантности
отношения толерантности  есть минимальная эквивалентность, включающая эту толерантность.
есть минимальная эквивалентность, включающая эту толерантность.
Теорема. Для того, чтобы произведение  отношений толерантности
отношений толерантности 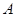 и
и 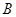 было толерантностью, необходимо и достаточно, чтобы
было толерантностью, необходимо и достаточно, чтобы 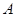 и
и 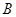 коммутировали. В этом случае
коммутировали. В этом случае 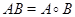 .
.
Доказательство. Симметрическое произведение  толерантностей
толерантностей 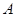 и
и 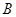 всегда будет толерантностью. Симметричность симметризованного произведения
всегда будет толерантностью. Симметричность симметризованного произведения 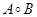 следует из того, что:
следует из того, что: 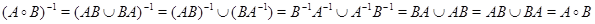 .
.
Можно ввести еще один вариант симметризованного произведения: 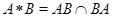 . Легко показать, что
. Легко показать, что 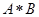 будет толерантностью, если
будет толерантностью, если 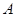 и
и 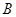 – толерантности.
– толерантности.
Полезно заметить, что для любого рефлексивного отношения 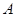 отношения
отношения  будут толерантностями.
будут толерантностями.
Классы толерантности
Изучим структуру пространств толерантности и попробуем различными способами представить, как устроены произвольные пространства толерантности. Общий результат состоит в том, что любое отношение толерантности может быть задано набором признаков так, что толерантные элементы – это те, которые имеют общие признаки.
Охарактеризуем некоторую совокупность объектов признаками. Возьмем множество 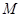 всех этих объектов и множество
всех этих объектов и множество  всех возможных признаков. Установим теперь соответствие
всех возможных признаков. Установим теперь соответствие 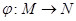 , сопоставляющее каждому объекту из
, сопоставляющее каждому объекту из 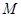 все те признаки, которыми он обладает. Наоборот, любое соответствие
все те признаки, которыми он обладает. Наоборот, любое соответствие 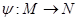 можно интерпретировать как присвоение некоторым объектам (элементам множества
можно интерпретировать как присвоение некоторым объектам (элементам множества 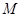 ) некоторых признаков (элементов из
) некоторых признаков (элементов из 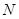 ).
).
Строгое понятие "соответствие" позволяет придать точный смысл обиходному выражению "иметь признаки". В 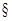 1 мы показали, что всякое всюду определенное на
1 мы показали, что всякое всюду определенное на 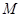 соответствие
соответствие  задает на множестве
задает на множестве 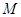 отношение толерантности
отношение толерантности 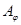 , определяемое как совпадение хотя бы одного признака (наличие общего признака).
, определяемое как совпадение хотя бы одного признака (наличие общего признака).
Покажем, что любое отношение толерантности можно задать таким образом. Более того, существует некоторая каноническая совокупность признаков, которая строится по данному отношению толерантности независимо от способа его конкретного задания.
Отношение толерантности 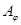 на множестве
на множестве 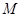 может быть определено на языке покрытий. (Система множеств
может быть определено на языке покрытий. (Система множеств 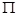 называется покрытием множества
называется покрытием множества 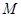 , если
, если 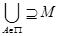 .)
.)
Пусть 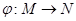 – всюду определенное соответствие. Сопоставим каждому "признаку"
– всюду определенное соответствие. Сопоставим каждому "признаку" 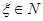 множество
множество 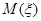 всех элементов из
всех элементов из 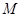 , обладающих признаком
, обладающих признаком 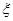 , т.е. множество
, т.е. множество 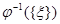 . Система всех множеств
. Система всех множеств 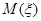 образует покрытие множества
образует покрытие множества 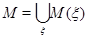 , поскольку любой элемент
, поскольку любой элемент 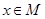 входит в некоторое
входит в некоторое 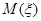 . Легко видеть, что
. Легко видеть, что 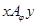 тогда и только тогда, когда существует такой признак
тогда и только тогда, когда существует такой признак 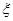 , что
, что 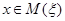 и
и 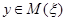 . Таким образом, толерантность
. Таким образом, толерантность 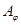 может быть задана так:
может быть задана так: 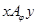 , если
, если  и
и 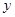 принадлежат некоторому общему классу покрытия
принадлежат некоторому общему классу покрытия 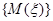 .
.
Перейдем к формальным построениям. Пусть задано пространство толерантности 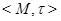 .
.
Определение
Множество  называется предклассом в
называется предклассом в 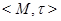 , если любые два его элемента
, если любые два его элемента 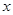 и
и 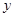 толерантны, т.е. для них выполнено соотношение:
толерантны, т.е. для них выполнено соотношение: 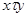 .
.
Лемма. Для того, чтобы два элемента 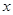 и
и 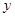 были толерантны, необходимо и достаточно, существовал предкласс
были толерантны, необходимо и достаточно, существовал предкласс 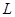 , содержащий оба этих элемента.
, содержащий оба этих элемента.
Доказательство. Если 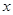 и
и 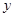 лежат в предклассе
лежат в предклассе 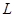 , то по определению 2.3.1 предкласса выполнено соотношение
, то по определению 2.3.1 предкласса выполнено соотношение 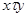 . Если
. Если 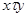 , то множество
, то множество 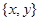 само образует предкласс, так как, кроме исходного соотношения, выполнены также соотношения
само образует предкласс, так как, кроме исходного соотношения, выполнены также соотношения 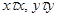 и
и 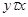 .
.
Определение
Множество 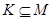 называется классом толерантности в
называется классом толерантности в 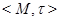 , если
, если 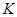 есть максимальный предкласс.
есть максимальный предкласс.
Это значит, что любое множество 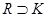 уже не является предклассом. Или, иначе,
уже не является предклассом. Или, иначе, 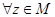 , не входящего в
, не входящего в 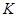 , существует элемент
, существует элемент 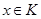 , не толерантный к
, не толерантный к 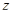 .
.
Лемма. Всякий предкласс содержится хотя бы в одном классе 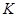 .
.
Доказательство. Проведем его лишь для случая, когда само множество 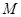 конечно. Пусть
конечно. Пусть 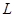 – предкласс. Если
– предкласс. Если 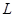 – есть класс, то лемма доказана. Если
– есть класс, то лемма доказана. Если 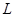 – не класс, то в множестве
– не класс, то в множестве 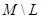 существует элемент
существует элемент 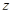 , толерантный ко всякому элементу из
, толерантный ко всякому элементу из 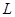 . Добавим такой элемент
. Добавим такой элемент  к
к 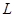 , т.е. рассмотрим множество
, т.е. рассмотрим множество 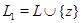 . Тогда
. Тогда 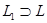 и
и 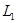 снова является предклассом. Либо
снова является предклассом. Либо  – класс, либо мы продолжаем дальше этот процесс расширения предкласса до класса. Поскольку множество
– класс, либо мы продолжаем дальше этот процесс расширения предкласса до класса. Поскольку множество 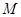 конечно, то через конечное число шагов наше построение класса закончится.
конечно, то через конечное число шагов наше построение класса закончится.
Следствие. Всякий элемент 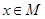 содержится в некотором классе, т.е. система классов толерантности образует покрытие множества
содержится в некотором классе, т.е. система классов толерантности образует покрытие множества 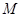 .
.
Действительно, в силу рефлексивности,  и множество
и множество 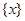 , состоящее из одного элемента
, состоящее из одного элемента 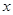 , образует предкласс.
, образует предкласс.
Лемма
Для того, чтобы два элемента 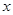 и
и 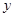 были толерантны, необходимо и достаточно, чтобы существовал класс, содержащий оба этих элемента.
были толерантны, необходимо и достаточно, чтобы существовал класс, содержащий оба этих элемента.
Все подготовлено к тому, чтобы сформулировать и доказать основную классификационную теорему.
Теорема. Пусть 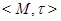 – произвольное пространство толерантности, а
– произвольное пространство толерантности, а 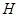 – множество всех его классов толерантности. Тогда существует отображение
– множество всех его классов толерантности. Тогда существует отображение 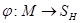 такое, что элементы из
такое, что элементы из 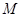 толерантны в том и только в том случае, когда толерантны их образы в
толерантны в том и только в том случае, когда толерантны их образы в 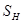 .
.
Доказательство. Выберем в качестве  отображение, которое каждому элементу
отображение, которое каждому элементу 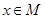 сопоставляет множество
сопоставляет множество 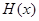 , состоящее из всех содержащих его классов. По следствию из леммы 2.3.2
, состоящее из всех содержащих его классов. По следствию из леммы 2.3.2 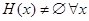 . По лемме 2.3.3 отношение
. По лемме 2.3.3 отношение  выполнено в том и только в том случае, когда
выполнено в том и только в том случае, когда 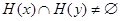 , т.е.
, т.е. 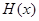 и
и  содержат общий класс.
содержат общий класс.
Если  – конечно, то количество всех его подмножеств конечно и поэтому конечно пространство
– конечно, то количество всех его подмножеств конечно и поэтому конечно пространство 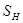 . Поэтому вместо отображения
. Поэтому вместо отображения 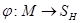 можно взять отображение
можно взять отображение 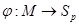 , где
, где 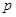 – число классов толерантности в
– число классов толерантности в 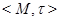 , которое каждому элементу
, которое каждому элементу 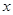 сопоставляет множество номеров, содержащих его классов:
сопоставляет множество номеров, содержащих его классов:  (здесь
(здесь  ).
).
Толерантность элементов 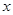 и
и 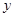 означает, что среди номеров, сопоставленных элементам
означает, что среди номеров, сопоставленных элементам 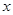 и
и 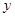 согласно
согласно  , есть хотя бы один общий. Т.е.
, есть хотя бы один общий. Т.е.  и
и 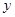 имеют общий числовой признак. Рассмотрим всюду определенное соответствие
имеют общий числовой признак. Рассмотрим всюду определенное соответствие  , которое каждому
, которое каждому 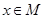 сопоставляет все классы, в которые он входит. Из леммы 2.3.3 следует, что
сопоставляет все классы, в которые он входит. Из леммы 2.3.3 следует, что 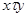 равносильно тому, что у
равносильно тому, что у 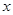 и y
и y 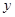 имеется общий образ в
имеется общий образ в  .
.
(Л. Кальмар – С. Якубович) Теорема. Произвольное отношение толерантности 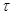 на множестве
на множестве  можно задать как отношение
можно задать как отношение 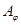 с помощью некоторого всюду определенного соответствия
с помощью некоторого всюду определенного соответствия 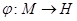 .
.
Дата: 2019-07-30, просмотров: 294.