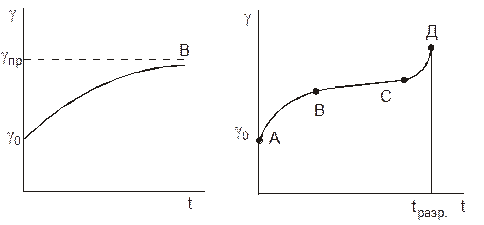
Прежде всего отметим, что ползучесть может протекать как с уменьшающейся, так и с возрастающей скоростью. В первом случае её называют затухающей, а во втором – незатухающей. В обоих случаях деформация складывается из двух слагаемых: мгновенной деформации  g _o , возникающей в теле сразу после приложения нагрузки t = const, и деформации, развивающейся во времени: g = g _o + g ( t ).

Слагаемое g( t ) при развитии затухающей ползучести стремится к некоторому предельному значению g_пр (рис. 14 а).

Незатухающая ползучесть (рис. 14 б) включает в себя три стадии: стадия затухающей неустановившейся ползучести (участок АВ, d g / dt  ® 0), стадия установившегося течения (участок ВС, g » const), стадия прогрессирующего течения (участок СД). Развитие третьей стадии отличается ростом скорости деформации и приводит к хрупкому или вязкому разрушению (точка Д на графике).

Развитие сдвиговых деформаций при выполнении условия t = const в различных горных породах протекает по-разному. Основные типы горных пород по виду кривой ползучести делят на два типа (рис.15). Для горных пород первого (I) типа увеличение γ имеет ограниченный характер: деформация ползучести растет по экспоненциальному закону и стремится к определенному пределу (глинистые и песчанистые сланцы, песчаник и пр.). Особенностью развития деформации ползучести у горных пород второго (II) типа является то, что на кривых ползучести не прослеживается предельной деформации: увеличение γ происходит неограниченно (галит, карналлит, уголь и пр.). Скорость деформации горных пород второго типа пропорциональна приложенному напряжению.

Реологические свойства го-рных пород первого типа отображает модель Пойнтинга–Томсона. Модель Максвелла достаточно близка для описания реологического поведения горных пород второго типа: развитие ползучести в горных породах второго типа отличается от развития ползучести в теле Максвелла наличием экспоненциального участка в первые моменты деформирования.

С явлением ползучести тесно связана продолжительность «жизни» тела под нагрузкой (длительная прочность, статическая усталость). В этом случае развитие разрушения тела (горной породы) происходит при действии напряжений, величина которых меньше значения прочности, наблюдаемой при кратковременном нагружении.

Оба процесса, рассмотренных при знакомстве с деформационными особенностями тела Максвелла (ползучесть и релаксация напряжений) развиваются и в горных породах, слагаюших стенку скважины. Как известно, на стенке скважины наибольшего значения достигает тангенциальное напряжение σ_θ, а минимального – величина радиального сжатия σ_r. Величина геостатического напряжения σ_z принимает промежуточное значение. Другими словами, имеем следующие условия:

σ_θ  = σ₁ , σ₂ = σ_z,  σ_r = σ₃ .

Величина наиболее опасного для возникновения сдвигового разрушения главного касательного напряжения определится равенством

τ₂ = (σ_θ – σ_r) / 2.

Для различных глубин величина касательного напряжения τ₂ различна, но является постоянной величиной для каждого конкретного значения глубины, т.е. выполняется условие развития ползучести              τ₂ = const. Величина напряжения τ₂ определит то или иное развитие ползучести: если касательные напряжения сопоставимы с величиной прочности горной породы на сдвиг, то развитие сдвиговой деформации в горных пород стенки скважины может привести к возникновению осложнений как при бурении скважины, так и позже - на стадии ее эксплуатации.

Спуск в скважину обсадной колонны и ее цементирование приводит к фиксированию величины угловой деформации в горных породах стенки скважины: γ = const. В этих условиях происходит релаксация напряжений: величина механических напряжений в горных породах стенки скважины с течением времени снижается. Физические процессы, приводящие к снижению напряжений, связаны с растрескиванием горной породы стенки скважины.