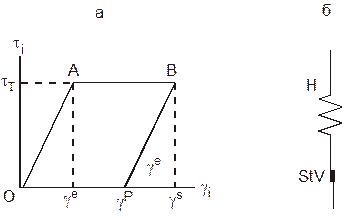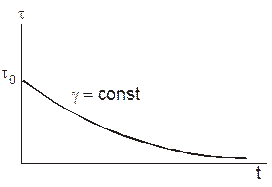В горных породах, не являющихся примером идеального тела, при деформировании развиваются все перечисленные виды деформаций одновременно: упругие, пластические, вязкие. По этой причине для описания их деформирования необходимо использовать более сложные механические модели.
Реологические свойства реальных тел можно моделировать с помощью различных сочетаний идеальных моделей. Существует параллельное и последовательное соединение идеальных моделей между собой. Параллельное соединение элементов обозначается знаком (½), а последовательное знаком (―) . Построение сложных реологических моделей происходит в соответствии с требованиями третьей аксиомы реологии.
Третья аксиома реологии: Существует иерархия реологических тел, согласно которой тело, низшее по иерархии, должно получаться из тела, высшего по иерархии, если в последнем приравнять нулю некоторые реологические параметры.
Третья аксиома реологии «ограничивает» построение новых реологических моделей: если при приравнивании к нулю реологических параметров модель нового реологического тела (высшего по иерархии) не обеспечивает возврат к уже известной модели, отражающей реологическое поведение тела, низшего по иерархии, то построение реологической модели нового тела было сделано неверно. Этот вывод относится и к дифференциальным уравнениям, описывающим поведение тел.
Сложные реологические тела
При последовательном соединении элементов полная нагрузка t приходится на каждый элемент, входящий в сложное тело:
t = t1 = ... = tn,
а полная деформация, возникающая в теле, складывается из деформаций, возникающих в отдельных составляющих сложное тело элементах:
g = g1 + ... + gn.
При параллельном соединении элементов деформации одинаковы для всех элементов:
g = g1 = ... = gn,
а полная нагрузка t складывается из нагрузок на отдельных элементах:
t = t1 + ... + tn.
Рассмотрим некоторые примеры построения сложных тел.
3.2.1. Упруго-пластическое тело Прандтля. Структурная формула тела Прандтля имеет вид Р = Н — StV. Реологическая диаграмма и механическая модель этого тела приведены на рис. 9. Данное тело при напряжениях, ниже предела текучести ti < tт, деформируется упруго по закону Гука ti = G.gI , а при ti = tт деформируется пластически. У этого тела деформация при разгрузке восстанавливается лишь частично. Общая деформация сдвига gs слагается из упругой ge и пластической частей:
|
Рис. 9. Деформационная кривая тела Прандтля: ge – упругая деформация, gp – пластическая деформация |
gs = ge + gp.
Упругопластическое тело Прандтля представляет собой тело, у которого отсутствует деформационное упрочнение. Для поддержания развития пластической деформации не требуется повышения напряжений ti до значений, превышающих предел текучести tт: достаточно поддерживать напряжения, равные пределу текучести.
|
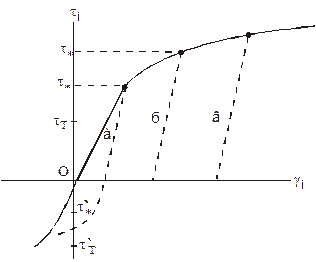
Рис. 10. Деформирование упругопластического тела, обладающего упрочнением
|
На рис.10 приведена зависимость интенсивности касательных напряжений ti от интенсивности сдвиговой деформации gi для упругопластического материала, обладающего деформационным упрочнением. При деформировании такого материала за начальной величиной предела текучести tт в материале начинает накапливаться остаточная деформация gp. Уменьшению напряжений ti на этом участке деформирования соответствует процесс разгрузки, происходящий по упругому закону (пунктирные линии а, б, в, на рис. 10). Новое повышение напряжений ti приводит к увеличению предела текучести до значения t* > tт. Это и есть упрочнение, связанное с развитием пластической деформации.
В таком материале наблюдается и эффект Баушингера: величина обратного (при растяжении материала) предела текучести (упругости) снижается t*' < tт' (рис. 10).
3.2.2. Вязкоупругое тело Максвелла, ползучесть и релаксация напряжений. Структурная формула тела Максвелла М = H — N (рис. 11 а). Реологическое уравнение, соответствующее этой структурной формуле, представляется следующим образом
gM = gH + gN,
где gH, gN – деформация элемента модели тела Гука, Ньютона. Аналогичный вид имеет и формула для скорости сдвиговой деформации в теле Максвелла:
(dgi/dt)M = (dg/dt)H + (dg/dt)N,
где (dg/dt)H, (dg/dt)N - скорость сдвига в телах Гука и Ньютона.
|
Рис. 11. Модели тела Максвелла (а) и тела Пойнтинга–Томсона (б)
|
Подставляя в выражение для скорости сдвиговой деформации тела Максвелла значения скоростей деформаций тел Гука (dg/dt = dt/dt / G) и Ньютона (см. первое уравнение в (8)), получим дифференциальное реологическое уравнение тела Максвелла:
t + Т dτ/dt = h dg/dt (9)
где T = h/ G – время релаксации, dim T = с. Время релаксации T является важным реологическим параметром.
При постоянном напряжении dτ/dt = 0 и тело Максвелла превращается в тело Ньютона, т.е. тело ведет себя как вязкая жидкость. Рост деформации в теле Максвелла с течением времени t происходит по линейному закону
g = tt/h + gо,
|
Рис. 12. Развитие деформации ползучести в теле Максвелла
|
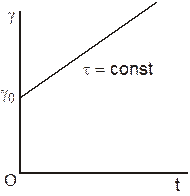
где g о – величина деформации в момент времени t = 0. Этот процесс называется ползучестью (рис. 12).
При постоянной деформации (g = const) решение уравнения (9) имеет следующий вид:
t = tоe–t/T ,
где tо есть начальное напряжение сдвига, t – время действия нагрузки.
|
Рис. 13. Релаксация напряжений в теле Максвелла
|
В соответствии с последним уравнением напряжение в теле Максвелла релаксирует (уменьшаются) практически до нуля (рис. 13).
Скорость развития релаксации напряжений определяется величиной времени релаксации: чем меньше Т, тем в большей степени материал проявляет жидкостные свойства и наоборот, чем больше Т, тем более твердообразным является материал.
Тело Максвелла следует рассматривать, как упруговязкое тело (вязкая жидкость, обладающая упругими свойствами). Проявление твердообразных и вязких свойств тела Максвелла зависит от соотношения времени t действия нагрузки и времени релаксации: если t << T , то в теле возникает, главным образом, упругая деформация и тело ведет себя как тело Гука. Если же справедливо неравенство t >> T, то в теле в большей степени проявляются свойства ньютоновской жидкости и доминирует вязкая деформация.
3.2.3. Тело Пойнтинга–Томсона: РТ = М│H1 (рис.11 б). Структурная формула тела показывает, что в отличие от тела Максвелла в данном случае существует предел деформации, который определяется пружиной H1.
Дата: 2019-07-30, просмотров: 359.