Под понятием «сплошная среда» понимается модель такого тела, которое, хотя и состоит из отдельных атомов, молекул, частиц, но занимает пространство непрерывным, сплошным образом, без разрыва сплошности. Горная порода, строго говоря, является дискретной системой. Поэтому лучшей моделью горной породы являлась бы модель, статистически описывающая взаимодействие различных частиц, входящих в её состав, с учетом физического типа взаимодействия между этими частицами. Такая модель горной породы в настоящее время не построена.
Поскольку размеры структурных элементов, входящих в горную породу (минералы, поры), много меньше любого рассматриваемого массива горной породы, то для описания закономерностей изменения напряженно-деформированного состояния используются методы механики сплошной среды: рассматриваются напряжения и деформации в бесконечно малой области и, используя аппарат дифференциального и интегрального исчислений, переходят к рассмотрению напряжений и деформаций в теле большого объема.
2.1. Напряженно-деформированное состояние горных пород
2.1.1. Напряженное состояние в «точке». Прежде всего поясним, что под «точкой» мы понимаем физически бесконечно малый объём горной породы. В дальнейшем этот объём мы часто будем представлять в виде куба, параллелепипеда.
При действии на горную породу механических усилий, в ней возникает напряженное состояние, которое характеризуется вектором напряжений  . Численное значение напряжения определяется отношением F / S , где S – площадка внутри тела, на которую действует сила F. Под площадкой S понимается величина макроскопическая, но физически бесконечно малая.
. Численное значение напряжения определяется отношением F / S , где S – площадка внутри тела, на которую действует сила F. Под площадкой S понимается величина макроскопическая, но физически бесконечно малая.
Напряженное состояние в «точке» считается определенным, т.е. известным, если известна величина модуля вектора напряжений и направление его действия.
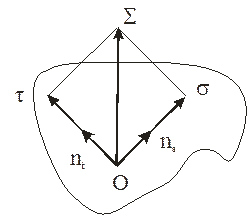
Для более детального описания напряженного состояния в «точке» в механике сплошной среды вводится понятие нормального σ и касательного τ напряжений. Из рис. 1 легко уяснить себе, что они представляют собой в двумерном случае, т.е. на плоскости.
|
Рис.1. Физический смысл нормального и касательного напряжений
|
Определяя нормальное напряжение σ , следует помнить, что в этом случае направление действия силы F совпадает с направлением единичного нормального вектора ns к площадке S; при определении касательного напряжения τ сила F действует в плоскости площадки S, т.е. действует по направлению единичного вектора nt, лежащего в плоскости площадки S (перпендикулярно нормали).
Суммарное действие нормального и касательного напряжений определяет направление действия вектора напряжений и его модуль S:
S = ns.s + nt·t,
S = (s2 + t2)0,5.
Напряженное состояние в «точке» 0 на площадке S определено, если известен вектор напряжения Σ или известны составляющие напряжения, т.е. напряжения σ и τ.
В трехмерном пространстве связь между составляющими напряжениями и компонентами вектора напряжений (проекции вектора напряжений S x , S y , S z на оси координат X , Y , Z ) имеет следующий вид:
Sx = nx.sx + ny.txy + nz.txz;
Sy = nx.tyx + ny.sy + nz.tyz;
Sz = nx.tzx + ny.tzy + nz.sz.
Здесь nx, ny, nz есть единичные вектора, направленные вдоль соответствующих осей координат, sx, sy, sz – нормальные напряжения, txy, tyz, tyz, tzx, tzy – касательные напряжения.
|
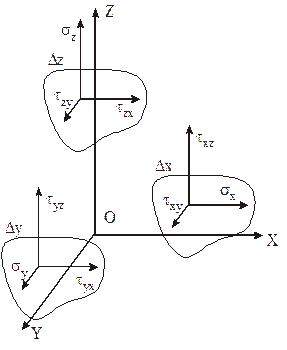
Рис. 2. Физический смысл компонент тензора напряжений
|
Из рис. 2 можно выяснить направление действия составляющих напряжений и порядок формирования нижних индексов: sx, sy , sz – нормальные напряжения, действующие на площадках Δx, Δy, Δz, перпендикулярных соответствующим координатным осям. Первый индекс в обозначении касательного напряжения указывает на принадлежность к соответствующей площадке, а второй - направление действия напряжения. Например, напряжение tzy действует на площадке Δz и направлено параллельно оси Y.
Суммарное действие составляющих напряжений Sx, Sy, Sz определяет величину модуля вектора напряжений и направление его действия
S = (Sx2 + Sy2 + Sz2)0.5;
S = nx.Sx + ny.Sy + nz.Sz.
Девять составляющих напряжений определяет тензор напряжений Tн, который имеет вид матрицы
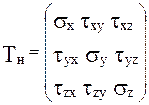 .
.
Между касательными напряжениями выполняются следующие равенства:
txy = tyx ; tzx = txz ; tyz = tzy .
Нормальные составляющие напряжения стремятся сократить (при сжатии), либо увеличить (при растяжении) линейные размеры деформируемого тела (стремятся изменить объем «точки», всего тела), касательные же составляющие напряжения стремятся сместить одну часть тела относительно другой (стремятся вызвать изменение формы «точки», тела), произвести сдвиговое разрушение тела.
Дата: 2019-07-30, просмотров: 380.