Прежде всего дадим геометрическую интерпретацию напряженного состояния изотропного тела, отобразив это состояние в трехмерном пространстве главных нормальных напряжений s₁, s₂, s₃ (рис. 4).

Начало координат соответствует отсутствию напряжений в теле. На осях координат лежат точки, отображающие простое растяжение или сжатие вдоль этих осей. На координатных плоскостях s₁s₂, s₂s₃, s₁s₃ расположены точки, отображающие плоское напряженное состояние.

Прямая, наклоненная под одинаковыми углами a (cos a = 3^-0,5) ко всем трем координатным осям, называется пространственной диагональю или гидростатической осью. Она определяет положение точек, соответствующих гидростатическому состоянию:

 s₁ = s₂ = s₃ = P.

Единичный вектор h, направленный вдоль гидростатической оси, определяется выражением

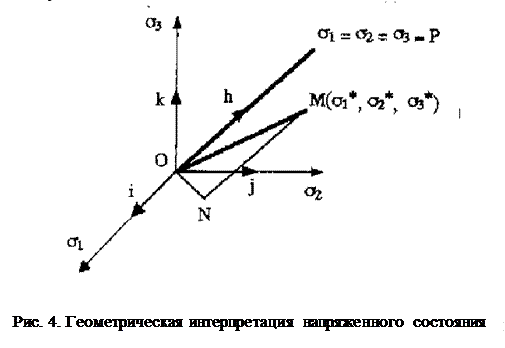
h = 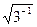(i + j + k),

где i, j, k – единичные вектора по направлению осей s₁, s₂, s₃ (рис. 4). Плоскость, проходящая через начало координат (т.О) и перпендикулярная вектору h, называется девиаторной плоскостью.

Так как направление нормали к девиаторной плоскости задается проекциями вектора h на оси координат, то из общего уравнения плоскости, проходящей через рассматриваемую точку с координатами (s₁^*, s₂^*, s₃^*),

A(s₁ – s₁^*) + B(s₂ – s₂^*) + C(s₃  – s₃^*) = 0,

где A = i, B = j, C = k, следует, что уравнение такой плоскости имеет вид

s₁ + s₂ + s₃ = 0.

Любая точка M трехмерного пространства s₁, s₂, s₃, имеющая координаты s₁^*, s₂^*, s₃^*, изображает некоторое напряженное состояние, характеризуемое главными напряжениями s₁, s₂, s₃ (Рис. 4).

Дадим геометрическую интерпретацию величинам s_ср и t_i. В качестве образа напряженного состояния мы будем рассматривать не точку М, а вектор ОМ, соединяющий начало координат О с точкой М(s₁, s₂, s₃):

ОМ = s₁^*i + s₂^* j + s₃^* k.

Если мы разложим вектор OM, характеризующий напряженное состояние, на составляющие MN и ON, параллельную и перпендикулярную гидростатической оси, соответственно, то составляющая MN определится выражением MN = ( OM ^h ) h , где

OM·h = (s₁^*i + s₂^*j + s₃^*k)· 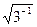(i + j + k) =

= (s₁^* + s₂^* + s₃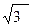^*)/ = s_ср× .

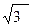Следовательно

                               MN = s_ср× 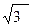h = s_ср(i + j + k),

т.е. проекция вектора напряжений OM на гидростатическую ось пропорциональна величине среднего напряжения s_ср.

Учитывая выражения для векторов MN и OM, можно записать

ON = OM – MN = (s₁^*i + s₂^*j + s₃^*k) – s_ср(i + j + k) =

= (s₁ – s_ср)i + (s₂ – s_ср)j + (s₃ – s_ср) k.

В последнем выражении величины, находящиеся в круглых скобках, представляют собой главные нормальные девиаторные напряжения

s₁ = (s₁ – s_ср),  s₂ = (s₂ – s_ср),  s₃ = (s₃ – s_ср).

Так как вектор ON по определению перпендикулярен гидростатической оси, то он должен лежать в девиаторной плоскости. Иначе говоря, проекции вектора напряжений OM (s₁^*, s₂^*, s₃^*) на девиаторную плоскость равна «вектору девиаторных напряжений» s₁ , s₂ , s₃. Иначе это можно выразить и так: точка N –  проекция точки M на девиаторную плоскость – изображает девиаторные напряжения, отвечающие точ-ке M . Любой вектор, принадлежащий девиаторной плоскости, характеризует девиатор напряжений какого-либо напряженного состояния M(s₁^*, s₂^*, s₃^*).

Радиальное расстояние между любой точкой, находящейся на гидростатической оси, и точкой M, расположенной на плоскости, параллельной девиаторной плоскости (в частности, расстояние между точкой O (начало координат) и точкой N, расположенной на девиаторной плоскости, проходящей через начало координат), найдем по известной (раздел курса математики «Аналитическая геометрия в пространстве») формуле

ON = 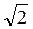·[(s₁^* – s₂^*)² + (s₂^* – s₃^*)² + (s₁^* – s₃^*)²] / 6 ]^0.5 = 2^0.5·t_i.

Иначе говоря, радиальное расстояние от гидростатической оси линейно зависит от интенсивности касательных напряжений t_i.

Появление вектора ON связано с неравнокомпонентностью напряженного состояния. Совершенно очевидно, что когда рассматриваемая точка M находится на гидростатической оси, то вектор главных девиаторных напряжений ON отсутствует в силу того, что s₁ = 0, s₂ = 0, s₃ = 0.

Так как увеличение радиального расстояния ON означает увеличение интенсивности касательных напряжений t_i , то для каждой точки M вектор ON определяет величину девиаторного напряжения, которое вызывает появление сдвигов, т.е. вектор ON определяет условие текучести для данного напряженного состояния.

Так как точка N является проекцией на девиаторную плоскость и любой другой точки, лежащей на прямой MN, то вектор главных нормальных девиаторных напряжений ON = s₁i  +  s₂j + s₃k является общим для всех точек любой прямой, перпендикулярной девиаторной плоскости. По этой причине если условие текучести выполняется для точки N , то оно будет выполняться и для всех точек бесконечной прямой NM. Все комбинации s₁, s₂, s₃, для которых выполняется данное условие текучести, образуют на девиаторной плоскости кривую текучести. Кривая текучести в девиаторной плоскости является направляющей цилиндра, образующие которого параллельны гидростатической оси. В пространстве главных нормальных напряжений возникает цилиндр текучести.

РЕОЛОГИЯ ГОРНЫХ ПОРОД

Фундаментом реологии являются несколько аксиом. Содержащиеся в них утверждения получены экспериментально. При изучении реологии мы будем использовать не сами тензоры напряжений и деформаций, а их инварианты, которые являются суммарной характеристикой изменения объёма и формы деформируемых тел.

Представим, что в нашем распоряжении имеются три шара, сделанные из трех различных материалов: стальной, пластилиновый и водяной. С этими тремя шарами мы проделаем несколько мысленных опытов, ставя перед собой основную задачу: определить вид механического воздействия на шары, способный распознать материалы, из которых сделаны шары.

Сначала рассмотрим падение этих шаров с некоторой высоты на поверхность стола. Еще до проведения такого опыта мы уверенно скажем, что различие в материалах, из которых сделаны шары, никак себя не проявит при падении шаров. Лишь при соприкосновении шаров с поверхностью стола мы обнаружим, что шары сделаны из разных материалов: стальной шар отскочит от поверхности стола, пластилиновый - прилипнет к столу, капля воды растечется по поверхности стола. Соприкосновение шаров с поверхностью стола обнаруживает различное деформирование шаров.

Если внимательно осмотрим шар из пластилина, то легко обнаружим на его поверхности плоскую площадку - результат смятия пластилина при контакте с поверхностью стола. В этом случае говорят, что в пластилиновом шаре возникла остаточная пластическая деформация. На поверхности стального шара такой плоской поверхности не видно, но есть все же основания предполагать её наличие в момент контакта шара с поверхностью стола: после окончания контакта шара со столом сферическая форма стального шара была восстановлена и это явилось причиной отскока шара от поверхности стола. Стальной шар – носитель восстанавливающейся упругой деформации. Поведение водного шара также резко отличается от поведения стального и пластилинового шаров: течение водяного шара по поверхности стола означает наличие у него необратимой вязкой деформации.

Подведём промежуточный итог: действие напряжений, возникающих в шарах при соприкосновении с поверхностью стола, вызывает в них появление деформаций различной природы: в стальном шаре возникает упругая деформация, в пластилиновом шаре - пластическая деформация, а в водяном шаре возникает течение, или, по другому, вязкая деформация.

Обнаружив значительное отличие в поведении трех шаров при проведении простого опыта, мы все же не приблизились к пониманию главного: действие какого напряжения способно отличить материал одного шара от материала другого?

Рассмотрим теперь поведение трех шаров при гидростатическом давлении. Эксперименты показывают, что результатом действия небольшого гидростатического давления s_ср будет увеличение плотности и уменьшение объёма V шаров в соответствии с уравнением s_ср = K.e_ср на величину DV = 3s_срV/K, где K - коэффициент объёмного деформирования (модуль объёмного сжатия). Форма шаров останется неизменной. При снятии давления прежние объём и плотность полностью восстанавливаются. Этот экспериментальный факт лег в основу первой аксиомы реологии.