Переход к двухосному, а затем и трехосному нагружению образцов горных пород приводит к дальнейшему росту их прочности и увеличению энергоёмкости разрушения.

Учет трения, возникающего между сторонами развивающейся сдвиговой трещины, является сутью механических теорий прочности Кулона, Кулона–Навье, Мора. Знакомство с двумя первыми теориями прочности позволит лучше понять роль трения в увеличении прочности горных пород.                   

Механическая теория прочности Кулона

Разрушение образца горной породы, находящегося в сложном напряженном состоянии сжатия, происходит в результате развития в нем сдвиговой трещины. Происходит это тогда, когда предельного значения t_о достигнут главные касательные напряжения t₁, t₂, t₃ :

│ t₁ │ ³ t_о ,│ t₂ │ ³ t_о , │ t₃ │ ³ t_о ,

где t_о – прочность образца на сдвиг при растяжении и сжатии. Эту величину часто называют когезионной прочностью, сцеплением горной породы, так как она определяется не только энергией связей в структуре породы, характеризующих её адгезионную и когезионную прочность, но и с зацеплением частиц друг за друга при сдвиге, с затратой усилий на вращение, перемещение минеральных частиц в плоскости сдвига.

Так как среди главных касательных напряжений наибольшим является t₂, то условие разрушения, выраженное через главные нормальные напряжения, принимает вид

( s₁ – s₃) / 2 ³ t_о.

При выполнении записанного условия горная порода разрушается с образованием плоскости (поверхности) скольжения. Плоскость, по которой происходит сдвиговое разрушение, делит пополам угол между направлением действия напряжений s₁ и s₃, т.е. плоскость сдвига должна быть наклонена под углом 45⁰ к направлению действия осевой нагрузки. Экспериментально этот вывод не подтверждается: в экспериментах на сжатие плоскость сдвига составляет с направлением наибольшего нормального напряжения угол, меньший 45⁰.

Если же приведенное выше условие разрушения не выполняется, но нагрузка t₂  действует длительное время, то в зависимости от величины t₂ образец горной породы может разрушиться спустя какое-то время в результате развития в образце незатухающей ползучести (если t₂ велико), но если величина нагрузки мала, то развитие затухающей ползучести обеспечивает стабилизацию деформации образца во времени и разрушения не произойдет.

Серьезным недостатком теории Кулона является содержащееся в ней предположение о том, что материал обладает одинаковым сопротивлением растяжению и сжатию.

Механическая теория прочности Кулона–Навье

Уже Кулон предполагал, что на процесс разрушения при сжатии тела оказывает влияние не только сцепление t_о, но и «внутреннее трение», появление которого связано с трением противоположных сторон сдвиговой трещины.

Основное положение теории Кулона–Навье: нормальное напряжение s, действующее в плоскости сдвигового разрушения, повышает сопротивление тела сдвигу на величину, пропорциональную величине этого нормального напряжения. Разрушение твердого тела в этом случае произойдет тогда, когда касательное напряжение, действующее в плоскости сдвига, достигнет величины

                                                      t = t_о + m·s,                                       (12)

где m.s – напряжение трения, m – постоянная материала, именуемая как «коэффициент внутреннего трения». Внутреннее трение можно рассматривать как дополнительные силы сцепления в горной породе, возникающие между поверхностями сдвиговой трещины под действием среднего нормального напряжения.

Из формулы (12) следует, что величина напряжения сдвига  t линейно зависит от нормального давления, действующего в этой же плоскости. На основании этого предположения Кулон нашел, что угол b  между осью нагружения и плоскостью разрушения определяется выражением

b = 45^о –  j / 2,

где tg j = m.

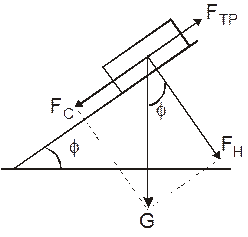
Рис. 16. Силы, действующие на груз, находящийся на наклонной плоскости

Слагаемое m.s в выражении (12) для t по форме записи аналогично выражению для силы трения на наклонной плоскости, вызванной нормальной реакцией, и по этой причине коэффициент m назван коэффициентом внутреннего трения. Поясним это с помощью рис.16, на котором изображен груз весом G, находящийся на наклоненной под углом j  к горизонту плоскости.

При малых значениях угла j груз не в состоянии скользить по плоскости из-за наличия силы трения F_тр между грузом и плоскостью. В этом случае сила трения F_тр превосходит величину силы скольжения F_с.

По определению имеем F_тр = m.F_н, где F_н – нормальная компонента силы G или прижимающая сила, m – коэффициент трения. Движение груза по наклонной плоскости начнется при увеличении угла j и достижении силой скольжения величины силы трения F_с = F_тр .

Величина сил F_н и F_с легко находится через вес груза: F_н = G cosj  и F_с = m.F_н. Из равенства  m.G ·cos j = G·sin j  определим коэффициент внутреннего трения   m   через угол j :

                                                  m = tg j.

Термин «внутреннее трение» следует понимать как способность горной породы повышать сопротивление разрушению под влиянием среднего нормального напряжения сжатия s_ср, действующего в образце (на плоскости сдвига увеличиваются силы адгезионного взаимодействия между минеральными частицами, растет сила трения).

К физической особенности развития трещин сдвига в горных породах следует отнести образование на плоскости сдвига порошкообразного материала, обладающего высокой дисперсностью.

Наличие жидкости в горной породе изменяет развитие разрушения, т.к. внешняя нагрузка воспринимается уже не только твердым скелетом породы, но и жидкостью, находящейся в порах. Если геометрия порового пространства горной породы обеспечивает дренируемость жидкости, то под действием напора Р_n / g_ж, где Р_n – давление жидкости в поре, g_ж – удельный вес жидкости, произойдет фильтрация жидкости из образца, из очага разрушения. Это вызовет уплотнение породы, при этом все меньшая часть внешней нагрузки будет восприниматься жидкостью. При полном удалении жидкости из образца критерий разрушения будет иметь вид (12), но с несколько иными числовыми значениями слагаемых.

Критерий Кулона–Навье для пористых горных пород, насыщенных недренируемой жидкостью, глин имеет иной вид

                                        t = t_о + (s_ср – Р_n)· tg j.                                             (13)

Из уравнения (13) следует, что поровое давление Р_n не уменьшает прочность сцепления породы t_о, а снижает величину слагаемого, связанного с действием нормального напряжения. Это означает, что рост порового давления создает условия для преждевременного наступления формоизменения, стимулирует сдвиговую неустойчивость горной породы: снижает суммарное сопротивление сдвигу. Подчеркнем, что рассмотренные явления не оказывают влияния на изменение величины коэффициента трения: жидкость, находящаяся в порах под высоким давлением, в развивающихся сколах не служит смазкой. Поровая жидкость является смазкой только в случае проникновения её на адгезионную границу. Заметим, что появление на адгезионных границах жидкости (воды) может происходить вследствие дегидратации минералов, входящих в состав горных пород.

Величина

s_ср – Р_n = s_эфф,

входящая в состав второго слагаемого формулы (13), называется эффективным напряжением. Увеличение порового давления обеспечивает снижение напряжения s_ср, действующего между твердой компонентой горной породы, приводит к снижению эффективного нормального напряжения. Появление эффективного нормального напряжения препятствует закономерному уплотнению горной породы с увеличением глубины залегания пород. Появление аномального уплотнения свойственно горным породам, имеющим большую пористость. В первую очередь, это отличает глинистые горные породы, которые не только имеют большую пористость, но и обладают способностью к образованию связанной воды. Последнее препятствует отжиму воды при сжатии глинистой горной породы. По этой причине критерий Кулона–Навье для глинистых горных пород имеет вид (13).