Дедуктивные умозаключения, как наиболее показательный вид данной формы мышления, – такие, у которых между посылками и выводом или заключением имеется отношение логического следования.
Типичным примером дедуктивного умозаключения является простой категорический силлогизм (греч. sillogismos – выведение следствия), являющий собой форму дедуктивного опосредованного умозаключения, в котором из двух истинных категорических суждений, связанных средним термином, при соблюдении правил вывода следует вывод или заключение. Категорические суждения – такие, в которых мысль утверждается или отрицается вполне определенно, без всяких условий, и которые имеют субъектно-предикатную структуру.
Например (простой категорический силлогизм):
все кенгуру (М) – сумчатые млекопитающие (Р), – большая посылка;
это животное (S) – кенгуру (М), – меньшая посылка;
это животное (S) – сумчатое млекопитающее (Р), – вывод/заключение.
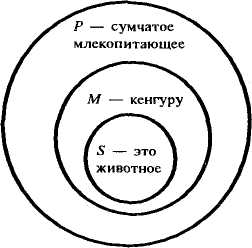
Входящие в состав силлогизма понятия называются терминами силлогизма. В представленном примере терминами являются: Р («сумчатое млекопитающее») – больший термин, предикат заключения; М («кенгуру») – средний термин; S («это животное») – меньший термин, субъект заключения.
М служит в посылках для связывания S и Р, и отсутствует в заключении.
Посылка, содержащая предикат заключения (больший термин), называется большей посылкой. Посылка, содержащая субъект заключения, т.е. меньший термин, называется меньшей посылкой.
Три понятия, входящие в силлогизм, называются: Р – больший термин (с большим объемом), М – средний термин, S – меньший термин (с меньшим объемом). Средний термин (М) – это термин, повторяющийся в обеих посылках, посредством которого они связываются в единое умозаключение.
Например:
все люди (М) – смертны (Р);
Сократ (S) – человек (М);
Сократ (S) – смертен (Р).
Простой категорический силлогизм имеет четыре фигуры, т.е. формы, которые различаются по положению среднего термина (М) в посылках:
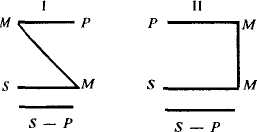
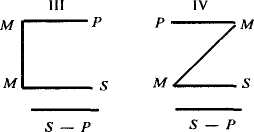
Примеры фигур простого категорического силлогизма:
Первая фигура силлогизма (Ι), по которой можно получить выводы всех остальных видов суждения:
все цветы (М) – растения (Р);
роза (S) – цветок (М);
роза (S) – растение (Р).
Вторая фигура силлогизма (ΙΙ), по которой можно получить только отрицательный вывод:
все кошки (Р) – млекопитающие (М);
это животное (S) не является млекопитающим (М);
это животное (S) не является кошкой (Р).
Третья фигура силлогизма (ΙΙΙ), вывод по которой – частное суждение:
все киты (М) – млекопитающие (Р);
все киты (М) – водные животные (S);
некоторые водные животные – млекопитающие.
Четвертая фигура силлогизма (ΙV) не дает вывода или вывод имеет слишком ограниченное познавательное значение:
все киты (Р) – млекопитающие (М);
ни одно млекопитающее (М) не является рыбой (S);
ни одна рыба (S) не является китом (Р).
Или:
депортация мирного населения (Р) – преступление против человечности (М);
преступление против человечности (М) – общественно опасное деяние (S);
некоторые общественно опасные деяния (S) являются депортацией мирного населения (Р).
Ход рассуждения по четвертой фигуре для процесса рассуждения не типичен, а познавательная ценность вывода/заключения невелика.
Существуют правила фигур простого категорического силлогизма.
Правила по первой фигуре: большая посылка должна быть общей, меньшая посылка должна быть утвердительной.
Правила по второй фигуре: большая посылка должна быть общей, одна из посылок должна быть отрицательной.
Правила по третьей фигуре: меньшая посылка должна быть утвердительной, вывод должен быть частным.
Правила по четвертой фигуре (общеутвердительных выводов не дает): если большая посылка утвердительная, то меньшая должна быть общей;
если одна из посылок отрицательная, то большая посылка должна быть общей;
если меньшая посылка утвердительная, то вывод частный.
Простые категорические силлогизмы, соответствующие этим правилам, являются правильными, не соответствующие – неправильными.
Существуют модусы фигур категорического силлогизма (лат. modus – мера, образ, способ), т.е. такие разновидности силлогизма, которые отличаются друг от друга качественной и количественной характеристикой входящих в них посылок и заключения. Имеется 19 правильных, т.е. дающих правильный вывод, модусов (качественно-количественных характеристик) простого категорического силлогизма в четырех фигурах.
По первой фигуре (буквы обозначают последовательно количество и качество большей посылки, меньшей и вывода/заключения): ААА, ЕАЕ, АII, ЕIО; представленный пример первой фигуры иллюстрирует модус ААА.
По второй фигуре: АЕЕ, АОО, ЕАЕ, ЕIО; представленный пример иллюстрирует модус АЕЕ.
По третьей фигуре: ААI, ЕАО, IАI, ОАО, АII, ЕIО; представленный пример иллюстрирует модус ААI.
По четвертой фигуре: ААI, АЕЕ, IАI, ЕАО, ЕIО; представленный 1-й пример иллюстрирует модус АЕЕ.
Категорические силлогизмы, являясь наиболее часто употребляемым умозаключением, встречаются в мышлении очень часто. Для того чтобы получить истинный вывод/заключение, необходимо брать истинные посылки и соблюдать правила категорического силлогизма.
Логическое основание всякого силлогического вывода называется аксиомой силлогизма. Она выражается так: все, что утверждается или отрицается про класс предметов в целом, распространяется на каждый элемент этого класса. Другими словами, что истинно относительно рода, то истинно относительно всех элементов или видов этого рода. И наоборот, что не присуще роду, то не присуще видам и элементам, в него входящим.
Структура силлогизма подчинена определенным логическим правилам, без соблюдения которых правильное его построение и получение вывода невозможно. Среди них выделяются правила терминов и правила посылок.
Правила терминов простого категорического силлогизма:
1) В каждом силлогизме должно быть только три термина (S, М, Р). Ошибку, называемую учетверением терминов, демонстрирует следующий пример:
движение вечно;
утренняя пробежка – движение;
утренняя пробежка вечна.
Здесь «движение» понимается в разном смысле – философском и обыденном. Или, например, из того, что: «собака бегает по двору», а «кошка сидит на дереве» нельзя сделать какого-либо правильного вывода, поскольку здесь – четыре разных термина (два субъекта и два предиката), а средний термин, который мог бы связать эти два суждения в единое рассуждение – отсутствует.
2) Средний термин должен быть распределен, по крайней мере, в одной из посылок, например:
некоторые грибы (М) ядовиты (Р);
шампиньоны (S) – грибы (М);
шампиньоны (S) – ядовиты (Р).
В данном примере средний термин – «грибы» не распределен ни в одной из посылок, т.е. взят не в полном объеме, и поэтому вывод ложный.
3) Термин распределен в выводе/заключении, только тогда, когда он распределен в посылках (термин, не распределенный в посылке, не может быть распределен и в выводе). Иначе в терминах вывода утверждалось бы больше, чем в терминах посылок, например:
все углы треугольника (M) равны в своей сумме 180° (P);
рассматриваемые углы (S) – углы треугольника (M);
рассматриваемые углы (S) в своей сумме составят 180° (P).
Вывод здесь не является истинным, поскольку могут быть рассмотрены не три, а два угла треугольника, сумма которых будет меньше 180°. Ошибочный вывод основывается на нарушении распределенности термина во второй посылке; предикат вывода в заключении распределен, а во второй посылке – нет, следовательно, произошло расширение большего термина (P вывода).
Правила посылок простого категорического силлогизма:
1) Из двух отрицательных посылок нельзя сделать никакого вывода. В этом случае все термины исключают друг друга, устраняя всякую объемную связь между ними, например:
киты не рыбы, а млекопитающие;
щуки не являются китами; (?)
2) Если одна из посылок отрицательная, то и вывод будет отрицательным, например:
всякое целенаправленное действие связано с полаганием цели;
ураган не связан с полаганием цели;
ураган не является целенаправленным действием.
3) Из двух частных посылок невозможно сделать вывод. В этом случае нельзя установить объемные отношения между терминами силлогизма, поэтому определенный вывод не получится, например:
некоторые животные – травоядные;
некоторые организмы – животные; (?)
4) Если одна из посылок частная, то и вывод будет частным, например:
некоторые пенсионеры – работают;
все работающие выполняют трудовые обязанности;
некоторые из тех, кто выполняют трудовые обязанности – пенсионеры.
Без соблюдения этих общих правил нельзя сделать правильный вывод.
3. Сокращенный, сложный и сложносокращенный силлогизмы
В мышлении и речи зачастую используется такой вид дедуктивного умозаключения как сокращенный категорический силлогизм или энтимема (греч. in tymes – в уме). Энтимемой называется сокращенный силлогизм, в котором пропущена одна из посылок или вывод. Здесь в явной форме не выражается какая-либо посылка или вывод, однако пропущенный элемент рассуждения подразумевается; т.е. некоторые посылки либо вывод здесь не формулируются в явной форме. Например: «Петров совершил мужественный моральный поступок, поэтому должен быть горд собой». Здесь пропущена большая посылка: «каждый человек, который совершает мужественный моральный поступок, может гордиться собой», представляющая собой общеизвестное, понятное положение, формулировать которое необязательно.
Поскольку энтимема – силлогизм, в котором в явной форме может быть не выражена какая-либо его часть, а не только большая посылка, необходимы следующие примеры энтимемы:
1) «свинец является металлом, поэтому свинец пластичен» (здесь пропущена большая посылка «все металлы – пластичны»);
2) «всякий порок заслуживает порицания, поэтому жадность должна порицаться» (здесь пропущена меньшая посылка «жадность есть порок»);
3) «все люди способны к логическому мышлению, а он – человек» (здесь пропущен вывод «потому он способен к логическому мышлению»).
Основанием для опускания посылок или вывода в силлогистических умозаключениях, осуществляемых в повседневных рассуждениях, является простота подразумевания этих (не выражаемых) элементов. Одно суждение еще не образует умозаключения, но суждение с выраженными в нем двумя частями силлогизма может представлять собой сокращенное умозаключение.
Энтимемами в мышлении и речи пользуются чаще, чем полными категорическими силлогизмами. При восстановлении энтимемы надо, во-первых, определить, какое суждение является посылкой, а какое – выводом. Посылка обычно стоит после союзов «так как», «потому что», «ибо» и т.п., а вывод стоит после слов «следовательно», «поэтому», «потому» и т.д.
В мышлении также встречаются не только полные или сокращенные силлогизмы, но и сложные силлогизмы, состоящие из двух, трех или большего числа простых силлогизмов, определенным образом связанных между собой. Эти цепочки силлогизмов называются полисиллогизмами. Итак, полисиллогизмом или сложным силлогизмом называются два или несколько простых категорических силлогизмов, связанных друг с другом таким образом, что вывод/заключение одного из них становится посылкой другого.
Например:
все растения – живые организмы;
все цветы – растения;
все цветы – живые организмы (вывод 1). — полисиллогизм
Роза – цветок;
роза – живой организм (вывод 2).
В логике различают прогрессивные и регрессивные полисиллогизмы. В прогрессивном (поступательном) полисиллогизме вывод предшествующего полисиллогизма (просиллогизма) становится большей посылкой последующего силлогизма (эписиллогизма). Пример прогрессивного полисиллогизма, представляющего собой цепочку из двух силлогизмов:
спорт (a) укрепляет здоровье (b);
гимнастика (c) – вид спорта (a);
гимнастика (c) укрепляет здоровье (b).
Аэробика (d) – разновидность гимнастики (c);
аэробика (d) укрепляет здоровье (b).
Схема прогрессивного/поступательного полисиллогизма:
все a суть b;
все b суть a;
все c суть b.
Все d суть c;
все d суть b.
В регрессивном (обратном) полисиллогизме вывод предшествующего полисиллогизма (просиллогизма) становится меньшей посылкой последующего силлогизма (эписиллогизма).
Например:
Все планеты (a) – космические тела (b);
Марс (c) – планета (a);
Марс (c) – космическое тело (b).
Или:
Все космические тела (b) имеют форму (d);
Марс (c) – космическое тело (b);
Марс (c) имеет форму (d).
Соединив их вместе и не повторяя дважды суждение «все c суть b», получаем схему регрессивного полисиллогизма для общеутвердительных посылок «все a суть b»:
все c суть a (все c суть b);
все b суть d;
все c суть b;
все c суть d.
Прогрессивный и регрессивный полисиллогизмы в мышлении и речи часто применяются в сокращенной форме – в форме соритов, умозаключений, состоящих из сокращенных силлогизмов. Сорит – это сложносокращенный силлогизм, в котором не высказываются, а только имеются в виду большие или меньшие посылки и все выводы, кроме последнего.
Существует два вида соритов: прогрессивный и регрессивный. Прогрессивный сорит – прогрессивный полисиллогизм, в котором пропущены все большие посылки, кроме первой, и все выводы, кроме последнего.
Например:
животное – субстанция;
четырехногое существо – животное;
конь – четырехногое существо.
Буцефал – конь;
Буцефал – субстанция.
Если восстановить пропущенные элементы, то получится:
животное – субстанция;
четырехногое существо – животное;
четырехногое существо – субстанция.
(Четырехногое существо – субстанция);
конь – четырехногое существо;
конь – субстанция.
(Конь – субстанция);
Буцефал – конь;
Буцефал – субстанция.
Прогрессивный сорит получается из прогрессивного полисиллогизма путем отбрасывания выводов предшествующих силлогизмов и больших посылок последующих. Он начинается с посылки, содержащей предикат вывода, и заканчивается посылкой, содержащей субъект вывода.
Например:
все продукты, содержащие витамины (a) – полезны для организма (b);
фрукты (c) – продукты, содержащие витамины (a);
яблоки (d) – фрукты (c);
яблоки (d) – полезны для организма (b).
Схема прогрессивного сорита:
все a суть b;
все c суть a;
все d суть c;
все d суть b.
Регрессивный сорит – регрессивный полисиллогизм, в котором пропущены все меньшие посылки, кроме первой, и все выводы, кроме последнего.
Например:
Буцефал (a) – конь (b);
конь (b) – четырехногое существо (c);
четырехногое существо (c) – животное (d).
Животное (d) – субстанция (e);
Буцефал (a) – субстанция (e).
Восстановление пропущенных элементов полисиллогизма аналогично предыдущему случаю.
Регрессивный сорит получается из регрессивного полисиллогизма путем отбрасывания вывода/заключения просиллогизмов и меньших посылок эписиллогизмов. В просиллогизме меняются местами посылки. Регрессивный сорит начинается с посылки, содержащей субъект вывода/заключения, и завершается посылкой, содержащей предикат вывода/заключения.
Пример регрессивного сорита:
все розы (a) – цветы (b);
все цветы (b) – растения (c);
все растения (c) имеют корни (d);
все розы (a) имеют корни (d).
Схема регрессивного сорита:
все a суть b;
все b суть c;
все c суть d;
все a суть d.
Сориты в мышлении и речи применяются чаще, чем полисиллогизмы, так как являются сокращенной формой полисиллогизмов.
В дедукции особенно ярко проявляется активность человеческой мысли.
Вопросы для самоконтроля знаний
1. Дайте определение умозаключения как сложной формы мышления.
2. Что такое рассуждение?
3. Что представляет собой логическая структура умозаключения?
4. Охарактеризуйте непосредственное и опосредованное умозаключение.
5. Назовите основные виды опосредованного умозаключения.
6. Дайте определение простого категорического силлогизма.
7. Охарактеризуйте структуру простого категорического силлогизма.
8. Что представляют собой фигуры простого категорического силлогизма?
9. Что представляют собой модусы простого категорического силлогизма?
10. Можно ли говорить об аксиоме простого категорического силлогизма?
11. Что представляет собой энтимема?
12. Что представляет собой полисиллогизм?
13. Охарактеризуйте прогрессивный и регрессивный полисиллогизм.
14. Что представляет собой сорит?
Литература
1. Богдановський І.В. Логіка: Опорний конспект лекцій / І.В. Богдановський, О.Г. Льовкіна. – К.: МАУП, 2004. – С. 61-73.
2. Войшвилло Е.К. Логика: Учебник для студентов высших учебных заведений / Е.К. Войшвилло, М.Г. Дегтярев – М.: Изд-во ВЛАДОС-ПРЕСС, 2001. – С. 333-387.
3. Гетманова А.Д. Логика: Для педагогических учебных заведений / А.Д. Гетманова. – М.: Новая школа, 1995. – С. 121-138.
4. Кириллов В.И. Логика: учебник для юридических вузов / В.И. Кириллов, А.А. Старченко. – М.: ТК Велби, Изд-во Проспект, 2008. – С. 119-143.
5. Логика: Учебное пособие для самостоятельного изучения дисциплины. – Харьков: ИД «ИНЖЭК», 2004. – С. 158-182.
6. Навчально-методичний посібник з дисципліни «Логіка» (для студентів всіх форм навчання за спеціальністю «Правознавство»). Укладач: Н.Г.Діденко. – Донецьк: ДонДУУ, 2004. – С. 37-48.
7. Подольска Є.А. Кредитно-модульний курс з філософії: філософія, логіка, етика, естетика, релігієзнавство. Навчальний посібник / Є.А. Подольска. – К.: Центр навчальної літератури, Інкос, 2006. – С. 403-405.
8. Разетдінов В.М. Логіка: навчально-методічний посібник (Кредитно-модульний курс) / В.М. Разетдінов. – Донецьк: ДонНУЕТ, 2010. – С. 105-117.
Дополнительная литература
1. Разетдинов В.М. Философия мышления / Основы философии. Учебник / Л.Н. Никитин, Л.А. Алексеева, Т.А. Андреева и др.; Под ред. д.филос.н., проф. Л.Н. Никитина. – Донецк: ДонНУЭТ, 2010. – С. 264-266.
2. Горский Д.П. Краткий словарь по логике / Д.П. Горский, А.А. Ивин, А.Л. Никифоров; Под ред. Д.П. Горского. – М.: Просвещение, 1991. – С. 36-38, 188-189.
3. Ивин А.А. Словарь по логике / А.А. Ивин, А.Л. Никифоров. – М.: ВЛАДОС, 1997. – С. 71-75, 344-345.
Тема 6. Индуктивное и традуктивное умозаключение
Вопросы
1. Индуктивное умозаключение, его логическая природа и основные виды.
2. Научная индукция.
3. Традуктивное умозаключение как умозаключение по аналогии.
1. Индуктивное умозаключение, его логическая природа
И основные виды
В дедуктивных умозаключениях осуществляется логический переход от общего знания к частному или от знания большей степени общности к знанию меньшей степени общности. Однако общее проявляется в конкретных единичных предметах. Познание общего предполагает изучение единичного, т.е. движение мысли от единичного, частного к общему, что и есть индукция.
В традиционной логике индукцией называется умозаключение от знания меньшей степени общности к знанию большей степени общности или логический переход от отдельных частных случаев к общему суждению.
В математической логике, индукцией называется такое умозаключение, которое дает вероятностное суждение.
Пример индуктивного умозаключения:
Енисей, Лена, Обь и Иртыш текут с юга на север;
Енисей , Лена, Обь, Иртыш – крупные реки Сибири;
все крупные реки Сибири текут с юга на север.
Итак, индуктивные умозаключения – такие, в которых из единичных или частных суждений выводятся в качестве вывода общие суждения. Это умозаключение представляет собой процесс логического вывода на основе перехода от частного положения к общему, т.е. на основе обобщения. Оно, как правило, дает не достоверные, а только правдоподобные выводы.
Например:
железо, медь, олово, свинец – тяжелее воды;
железо, медь, олово, свинец принадлежат к классу металлов;
все металлы – тяжелее воды.
Этот вывод был истинным до тех пор, пока не открыли калий.
В зависимости от избранного основания выделяют полную и неполную индукцию. Полной индукцией называется такое умозаключение, в котором общий вывод обо всех элементах класса делается на основе рассмотрения каждого элемента этого класса. В полной индукции изучаются все предметы данного класса, а посылками служат единичные суждения, например:
Земля вращается вокруг Солнца по эллиптической орбите;
Марс вращается вокруг Солнца по эллиптической орбите;
Юпитер вращается вокруг Солнца по эллиптической орбите;
Сатурн вращается вокруг Солнца по эллиптической орбите;
Плутон вращается вокруг Солнца по эллиптической орбите;
Венера вращается вокруг Солнца по эллиптической орбите;
Уран вращается вокруг Солнца по эллиптической орбите;
Нептун вращается вокруг Солнца по эллиптической орбите;
Меркурий вращается вокруг Солнца по эллиптической орбите;
Земля, Марс, Юпитер, Сатурн, Плутон, Венера, Уран, Нептун, Меркурий – планеты Солнечной системы;
все планеты Солнечной системы вращаются вокруг Солнца по эллиптической орбите (индуктивный вывод).
Посылками в полной индукции могут быть и общие суждения, например:
все моржи – водные млекопитающие;
все ушастые тюлени – водные млекопитающие;
все настоящие тюлени – водные млекопитающие;
моржи, ушастые тюлени, настоящие тюлени представляют семейство ластоногих;
все ластоногие – водные млекопитающие.
Полная индукция дает достоверный вывод, поэтому она часто применяется в математических и в других строгих доказательствах. Чтобы использовать полную индукцию, надо выполнить следующие условия:
1) точно знать число предметов или явлений, подлежащих рассмотрению;
2) убедиться, что признак принадлежит каждому элементу этого класса;
3) число элементов рассматриваемого класса должно быть невелико.
Разновидностью индуктивных выводов/умозаключений является математическая индукция, которая представляет собой важнейший метод доказательства в математике, основанный на принципе математической индукции. Он используется для доказательства истинности некоторого утверждения для всех натуральных чисел. Например, пусть: 1) свойство a имеет место при n = 1 (1 – обладает некоторым свойством – a); 2) из предположения о том, что свойством a обладает какое-либо натуральное число n, следует, что этим свойством a обладает и следующее за ним число n + 1 (индукционный шаг). Делается вывод, что свойством a обладает любое натуральное число (так называемая наследуемость свойства a в натуральном ряду чисел 1, 2, 3, ... n, n + 1). Математическая индукция как метод доказательства для последовательности натуральных чисел либо объектов, однозначно занумерованных натуральными числами, используется при выведении ряда формул: арифметической и геометрической прогрессий и др.
В свою очередь неполная индукция имеет место в тех случаях, когда, во-первых, невозможно рассмотреть все элементы интересующего класса явлений; во-вторых, если число предметов либо бесконечно, либо достаточно велико; в-третьих, когда рассмотрение упраздняет предмет, например: «все деревья имеют корни». Тогда рассматриваются не все случаи изучаемого предмета или явления, а вывод делается для всех. Например, при нагревании наблюдается расширение кислорода, водорода, азота и делается индуктивный вывод, что все газы при нагревании расширяются.
Итак, неполной индукцией называется такое умозаключение, в котором общий вывод о признаках всего класса предметов делается на основании исследования только лишь части предметов данного класса. По способам обоснования вывода она делится на три вида:
1) индукция через простое перечисление или популярная, где на основании повторяемости одного и того же признака у ряда однородных предметов и отсутствия противоречащего случая делается общий вывод, что все предметы этого класса обладают этим признаком. Например, на основе этой индукции считали, что все лебеди белые – до тех пор, пока в Австралии не обнаружили черных лебедей. Эта индукция дает вероятностный, а не достоверный вывод. На основе этой индукции народ вывел много примет: ласточки низко летают – быть дождю; если закат солнца красный, завтра будет ветреный день и др.;
2) индукция через анализ и отбор фактов, где исключается случайность обобщений, и изучаются специально отобранные, типичные предметы. Так вычисляют среднюю урожайность поля, судят о всхожести семян, о составе полезных ископаемых, о качестве больших партий товара. Например, при целенаправленном изучении свойств серебра, было обнаружено, что оно активирует кислород, уничтожающий бактерии, поэтому с помощью серебра очищают питьевую воду, применяют его при лечении ряда заболеваний;
3) научная индукция, в которой на основании познания существенных и необходимых признаков и связей части предметов определенного класса, делается общий вывод обо всех предметах класса. Здесь обобщение строится путем отбора необходимых и исключения случайных обстоятельств.
Научная индукция
Научная индукция – наиболее совершенный вид индукции. Вывод о признаках класса предметов делается в ней на основании исследования внутренней их обусловленности у части предметов данного класса. Научная индукция, в которой делается общий вывод обо всех предметах класса, имеет большое значение, поскольку позволяет формулировать общие суждения.
Научная индукция может давать достоверный вывод, хотя она и не охватывает все предметы изучаемого класса, а только их часть. Это объясняется тем, что здесь учитывается причинно-следственная связь. Так, с помощью научной индукции делается вывод: «всем людям необходима влага для их жизнедеятельности». Причиной излечивания от некоторых болезней при лечебном голодании является внутренняя саморегуляция организма, когда происходит общебиологическая перестройка организма человека.
Применение научной индукции позволило сформулировать многие научные законы. Так, например, закон Архимеда (являющийся одним из главных законов гидростатики) описывает свойство жидкости оказывать давление снизу вверх на погруженное в нее тело. С применением научной индукции получены и связанные с социологией законы развития общества.
Научная индукция опирается не столько на большое число исследованных фактов, сколько на всесторонность их анализа и установление причинной зависимости, выделение необходимых признаков и связей предметов. Поэтому научная индукция дает достоверный вывод. В ее основе – фиксация объективной причинно-следственной связи.
Причина – это явление или совокупность явлений, которые порождают другое явление как свое следствие. Причинная связь – это необходимая связь между явлениями, при которой за одним из них всякий раз следует другое. Первое явление называется причиной, второе – действием или следствием.
Причинная связь имеет необходимый характер, поскольку при наличии причины соответствующее ему действие/следствие обязательно происходит. Например, молния ударяет в дерево, оно раскалывается и обугливается. Идет дождь, и на земле образуются лужи. Начинает извергаться вулкан, и пепел засыпает город. Во всех этих случаях одно явление – причина – производит другое явление – свое закономерное следствие. При этом сама причинная связь еще не дана в опыте, она устанавливается посредством рассуждения.
В логике разработаны определенные методы таких индуктивных рассуждений, которые получили название методов индукции. Формулировка этих методов была дана в XVΙI веке английским философом Ф.Бэконом. Систематически они были исследованы в XIX веке английским философом и логиком Д.С.Миллем. Отсюда их наименование – «методы Бэкона – Милля».
Методы индукции опираются на следующие свойства причинной связи:
1) причина всегда предшествует следствию во времени;
2) причинная связь необходима: всякий раз, когда есть причина, неизбежно наступает и следствие;
3) причина порождает и обуславливает собой следствие. Без генетического понятия «порождение» нельзя отличить причину от повода, т.е. события, непосредственно предшествующего данному событию, делающему его возможным, но не порождающему и не определяющему его. Например, на веревке подвешен груз, веревка перерезается, груз падает. Перерезание веревки – только повод, а причина – земное притяжение. Если груз лежал бы на земле или находился в состоянии невесомости, он, лишившись подвески, не упал бы. Понятие порождения необходимо и для отличения причинной связи от постоянного следования явлений друг за другом, которое не есть причинно-следственная связь. Например, день наступает после ночи, но ночь не порождает день и не является его определяющей причиной;
4) с изменением интенсивности или силы действия причины соответствующим образом меняется интенсивность следствия;
5) причинность всеобща: не существует беспричинных явлений, в мире все возникает только в результате действия определенных причин.
Логические связи суждений о причинной связи изучает логика причинности. В логике разработаны каноны индукции (греч. canon – предписание), представляющие собой методы установления причинных связей между явлениями. Это было сделано Д.С.Миллем («каноны Милля»), который опирался на «таблицы открытий» Ф.Бэкона. В логике используются следующие индуктивные методы установления причинных связей:
1) метод единственного сходства заключается в том, что, если два и более случая исследуемого явления сходны только в одном обстоятельстве, то существует вероятность, что именно это обстоятельство и есть причина или часть причины данного явления. Так, если предшествующие обстоятельства АВС вызывают явление abc, а обстоятельства АDЕ – явление аde, то делается вывод, что А – причина а или что явления А и а причинно связаны. Например, желая установить, почему изучаемые маятники имеют одинаковый период колебания при различии материалов, различии их форм и других характеристик, обнаруживается единственное сходство между ними: все они имеют одинаковую длину. Отсюда делается вывод, что одинаковая длина маятников является причиной равенства периодов их колебаний. Этот метод можно квалифицировать как метод нахождения общего в различном;
2) метод единственного различия: если имеется случай, в котором исследуемое явление возникает, и случай, в котором оно не возникает, отличаются только одним обстоятельством, то оно, вероятно, и есть причина (часть причины) этого явления. Так, если предшествующие обстоятельства АВС вызывают явление abc, а обстоятельства ВС (явление А устраняется в ходе эксперимента) вызывают явление bc, то делается вывод, что А есть причина явления а. Основанием такого вывода служит исчезновение – а при устранении – А. Например, в спектре вещества, содержащего натрий, наблюдается желтая линия. При устранении натрия из этого вещества желтая линия исчезает. Отсюда вывод, что присутствие натрия в данном веществе есть причина желтой линии в наблюдаемом спектре; или в обычных условиях ускорение падения тел зависит от их удельного веса, а в безвоздушной среде те же тела будут падать с одинаковым ускорением. При организации этого эксперимента можно обеспечить полное сходство во всем, кроме одного обстоятельства – наличия либо отсутствия воздуха. Сопротивление воздушной среды есть причина падения тел с различным ускорением. Этот метод можно квалифицировать методом нахождения различного в сходном;
3) объединенный метод сходства и различия: если два или большее число случаев, когда наступает данное явление, сходны в одном обстоятельстве, в то время как два или более случаев, когда этого явления нет, различаются только тем, что данное обстоятельство отсутствует, то это обстоятельство и есть, вероятно, причина исследуемого явления. Этот метод представляет собой комбинацию двух первых методов, когда посредством анализа ряда случаев выявляется как сходное в различном, так и различное в сходном;
4) метод сопутствующих изменений: если с изменением одного – предшествующего явления (А) изменяется и другое – наблюдаемое явление (а), а остальные обстоятельства остаются неизменными, то между данными явлениями существует, вероятно, причинная связь, т.е. А есть причина а. Например, поскольку по мере увеличения температуры газа увеличивается его объем, можно сделать вывод, что между температурой и объемом есть причинная связь. Этим методом была установлена причинная зависимость величины морских приливов от сил притяжения луны и солнца. Другими словами, если изменение одного обстоятельства всегда вызывает изменение другого, то первое обстоятельство есть причина второго. Так, например, трение есть причина нагревания тела;
5) метод остатков: если сложная причина производит сложный результат – явление и известно, что часть причины вызывает определенную часть этого результата/явления, то остающаяся часть причины производит, вероятно, остальную часть результата/явления. Так, если из сложного явления (авс), вызываемого комплексом обстоятельств (АВС), исключить изученную часть, зависящую от уже известных обстоятельств, то остаток этого явления будет следствием оставшихся из комплекса АВС обстоятельств. Схема метода такова: явление авс вызывается обстоятельствами АВС; часть в явления авс вызывается обстоятельством В; часть с явления авс вызывается обстоятельством С; вероятно, часть а явления авс находится в причинной связи с обстоятельством А. Например, спектральным анализом установлено, что каждому химическому элементу в спектре соответствует определенная линия. В солнечном спектре была обнаружена линия ярко-желтого цвета, которую нельзя приписать ни одному известному на земле элементу. Этот элемент был назван гелием. Позднее был выделен газ, в спектре которого была обнаружена желтая линия, совпавшая с той, что была найдена в спектре солнца. Это открытие стало доказательством того, что выделенный газ есть гелий; или, например, такое рассуждение: увеличение населения страны зависит от двух основных факторов: естественного прироста населения (т.е. разности между рождаемостью и смертностью) и социального движения населения (т.е. разности между эмиграцией и иммиграцией). Если известна интенсивность общего роста и естественного прироста, то можно посредством вычитания из общего прироста населения получить результаты воздействия естественного прироста населения и таким образом получить величину социального прироста населения страны.
Нельзя отождествлять простую последовательность событий во времени с их причинной связью. В данном случае допускается логическая ошибка, которая называется «после этого, следовательно, по причине этого». Она является причиной многих суеверий. Например, солнечное затмение рассматривалось как причина ряда народных бедствий на том основании, что когда-то оно предшествовало войне, разгулу стихии, неурожайному году и т.п.
Основным условием истинности индуктивного умозаключения/вывода, как собственно и дедуктивного, является истинность посылок. Нарушение этого необходимого условия ведет к ошибкам в рассуждениях.
3. Традуктивное умозаключение как умозаключение по аналогии
Важнейшим видом опосредованных умозаключений является также традукция, представляющая собой аналогию. Традукция (лат. traductio – перемещение) или традуктивное умозаключение – это умозаключение от выясненного частного сходства между предметами к более глубокому и разностороннему сходству между ними; это умозаключение/рассуждение о принадлежности предмету определенного признака, свойства, отношения на основе его сходства в существенных признаках с другим предметом; это приписывание предмету свойства или перенос на него отношений, присущих другому предмету. Традуктивное умозаключение строится по принципу аналогии (греч. analogia – соответствие), т.е. установления сходства между предметами; согласно этой логике рассуждения: предметы, сходные в других свойствах, вероятно сходны и в данном свойстве. Другими словами такое – традуктивное рассуждение представляет собой умозаключение по аналогии.
Аналогия – это недедуктивное умозаключение, в котором вывод о принадлежности определенного признака предмету выводится на основании установления его сходства с другим предметом. Аналогия представляет собой переход к знанию той же степени общности, т.е. от единичных суждений – к единичным, от частных – к частным, от общих – к общим.
Аналогия неотъемлема от самой природы логического понимания фактической действительности, поскольку новое, неизведанное может быть осмыслено и понято через понятия и образы уже известного, познанного. Тем самым аналогия связывает нити известного с неизвестным и неизведанным.
Познавательное значение аналогии характеризуется рядом примеров научных открытий. Так, аналогия с насосом привела к идее непрерывной циркуляции крови; обнаруженные при изучении света явления интерференции и дифракции позволили сделать вывод о его волновой природе, поскольку ранее эти же свойства были выявлены у звука, волновой характер которого был уже установлен. Большую роль в открытии закона всемирного тяготения Ньютоном сыграла аналогия между падением яблока с дерева на землю и падением малых небесных тел. В процессе научного познания аналогия используется как умозаключение и метод познания: природа звука устанавливается по аналогии с морской волной, природа света – по аналогии со звуком, природа электричества – по аналогии со светом и т.д.
Аналогия может служить средством выдвижения новых идей и гипотез, быть методом решения задач путем сведения их к ранее решенным задачам.
Посредством аналогии происходит перенос информации с одного предмета (модели) на другой (прототип). Схема умозаключения по аналогии:
предмет А имеет признаки abcd;
предмет В имеет признаки abc;
вероятно, что предмет В имеет также и признак d.
При этом традуктивные выводы по аналогии, в результате которых достигается знание о признаках одного предмета на основании знания о том, что он имеет сходство с другими предметами – это выводы, как правило, вероятные, проблематические, которые, конечно, не являются единственным источником знания о мире как объективной действительности. Даже если посылки рассуждения по аналогии истинны, это еще не означает, что и его вывод будет истинным. Данные аналогии нуждаются в поверке на практике.
В зависимости от характера признака, переносимого с одного предмета на другой, различают аналогию свойств и аналогию отношений.
В аналогии свойств рассматриваются два предмета или два класса однородных предметов, а переносимыми свойствами выступают свойства самих этих предметов. Например: аналогия между Марсом и Землей, аналогия в симптомах протекания болезни у двух людей и др.
В аналогии отношений признаками, переносимыми с одного предмета (модели) или класса предметов на другой предмет (прототип) или класс предметов являются отношения, а не свойства; т.е. здесь фиксируются отношения между предметами или классами однородных предметов. Примером аналогии отношений является предложенная английским физиком Э.Резерфордом планетарная модель строения атома, которая построена на основе сходства отношений между солнцем и планетами и между ядром атома и вращающимися вокруг него по замкнутым орбитам электронами. На основе этой аналогии бионика занимается изучением объектов и процессов живой природы с целью использования таких знаний в новейшей технике.
По степени вероятности и достоверности выводов/заключений аналогия подразделяется на строгую, нестрогую и ложную.
Аналогия, которая дает достоверное или высоковероятное знание, считается строгой. Эта аналогия основывается на необходимой связи переносимого признака с признаками сходства. Научные аналогии обычно являются строгими. Так, формулировка признаков подобия треугольников базируется на строгой аналогии: «если три угла одного треугольника равны трем углам другого треугольника, то эти треугольники подобны» (подобие – вид аналогии). На умозаключении по строгой аналогии строится теория подобия, изучающая условия вероятности вывода по аналогии и лежащая в основе используемого наукой метода моделирования.
Моделирование – такая разновидность научной аналогии, при которой один из предметов (модель) подвергается исследованию в качестве имитации другого предмета (прототип/оригинал) и полученные знания о модели служат необходимыми посылками вывода по аналогии об оригинале.
При этом умозаключения по аналогии, нередкие в повседневной жизни, как правило, не очень строги, а то и просто поверхностны.
Аналогия, дающая только вероятное знание, считается нестрогой. Это такое уподобление, когда зависимость между сходными и переносимыми признаками мыслится лишь с большей или меньшей степенью вероятности.
Наиболее часто нестрогая аналогия применяется в общественно-исторических исследованиях, при характеристике политических ситуаций, когда крайне сложно установить необходимые связи между признаками сложных, противоречивых, развивающихся социальных явлений. От аналогий, имеющих место в художественной литературе, точность не требуется вообще, они оцениваются по силе художественного воздействия.
Повышение вероятности истинности выводов, полученных по аналогии, можно обеспечить, выполняя следующие требования:
1) число общих для образца (прототипа) и модели аналогии признаков должно быть как можно большим;
2) признаки, служащие основанием аналогии, должны быть существенными для сравниваемых предметов;
3) общие признаки должны охватывать различные стороны сравниваемых предметов;
4) переносимый признак должен принадлежать к тому же типу, что и признаки, составляющие основание аналогии, и быть связанным с ними;
5) наряду со сходством предметов необходимо учитывать и их различие.
Ложная аналогия возможна тогда, когда у сравниваемых предметов обнаружено малое количество сходных признаков, когда связь между сходными и переносимыми признаками установлена в слабой, поверхностной форме. Ложные аналогии могут делаться умышленно, используясь как софистический прием с целью ввести в заблуждение. Аналогии могут быть и внешними, надуманными, подменяющими действительные взаимосвязи вещей. На них опираются различные гадания, прорицания и суеверия.
В общем, характерная особенность умозаключений состоит в движении мысли от одних понятий и суждений к другим, от одного содержания знания – к другому. Сам логический акт умозаключения состоит не только в анализе уже имеющегося знания, но и в синтезе нового содержания (опыта, знания), в движении от известного и познанного к неизвестному и непознанному.
Вопросы для самоконтроля знаний
1. Дайте определение индуктивного умозаключения.
2. В чем заключается основное условие истинности индуктивного и дедуктивного умозаключений?
3. Что представляет собой полная индукция?
4. Что представляет собой неполная индукция?
5. Охарактеризуйте основные виды неполной индукции, их особенности.
6. Что представляет собой научная индукция?
7. Почему научная индукция может давать достоверный вывод?
8. На какие свойства причинной связи опираются методы индукции?
9. Что представляют собой каноны индукции?
10. Назовите методы установления причинных связей, которые используются в логике.
11. Дайте определение традуктивного умозаключения.
12. Что представляет собой аналогия как умозаключение?
13. Охарактеризуйте аналогию свойств и аналогию отношений, приведите соответствующие примеры.
14. Охарактеризуйте строгую и нестрогую аналогию, приведите соответствующие примеры.
15. Охарактеризуйте моделирование как разновидность научной аналогии.
Литература
1. Богдановський І.В. Логіка: Опорний конспект лекцій / І.В. Богдановський, О.Г. Льовкіна. – К.: МАУП, 2004. – С. 79-84.
2. Войшвилло Е.К. Логика: Учебник для студентов высших учебных заведений / Е.К. Войшвилло, М.Г. Дегтярев – М.: Изд-во ВЛАДОС-ПРЕСС, 2001. – С. 387-416.
3. Гетманова А.Д. Логика: Для педагогических учебных заведений / А.Д. Гетманова. – М.: Новая школа, 1995. – С. 161-172, 214-220.
4. Кириллов В.И. Логика: учебник для юридических вузов / В.И. Кириллов, А.А. Старченко. – М.: ТК Велби, Изд-во Проспект, 2008. – С. 161-194.
5. Логика: Учебное пособие для самостоятельного изучения дисциплины. – Харьков: ИД «ИНЖЭК», 2004. – С. 182-186.
6. Навчально-методичний посібник з дисципліни «Логіка» (для студентів всіх форм навчання за спеціальністю «Правознавство»). Укладач: Н.Г.Діденко. – Донецьк: ДонДУУ, 2004. – С. 48-52.
7. Подольска Є.А. Кредитно-модульний курс з філософії: філософія, логіка, етика, естетика, релігієзнавство. Навчальний посібник / Є.А. Подольска. – К.: Центр навчальної літератури, Інкос, 2006. – С. 405-406.
8. Разетдінов В.М. Логіка: навчально-методічний посібник (Кредитно-модульний курс) / В.М. Разетдінов. – Донецьк: ДонНУЕТ, 2010. – С. 117-124.
Дополнительная литература
1. Разетдинов В.М. Философия мышления / Основы философии. Учебник / Л.Н. Никитин, Л.А. Алексеева, Т.А. Андреева и др.; Под ред. д.филос.н., проф. Л.Н. Никитина. – Донецк: ДонНУЭТ, 2010. – С. 266-268.
2. Горский Д.П. Краткий словарь по логике / Д.П. Горский, А.А. Ивин, А.Л. Никифоров; Под ред. Д.П. Горского. – М.: Просвещение, 1991. – С. 13-14, 65-67.
3. Ивин А.А. Словарь по логике / А.А. Ивин, А.Л. Никифоров. – М.: ВЛАДОС, 1997. – С. 15-18, 124-128.
Дата: 2019-07-24, просмотров: 364.