При выводе основного уравнения молекулярно-кинетической теории молекулам задавали различные скорости. В результате многократных соударений скорость каждой молекулы изменяется по модулю и направлению. Однако из-за хаотического движения молекул все направления движения являются равновероятными, т. е. в любом направлении в среднем движется одинаковое число молекул.

По молекулярно-кинетической теории, как бы ни изменялись скорости молекул при столкновениях, средняя квадратичная скорость молекул массой m_о в газе, находящемся в состоянии равновесия при Т=const, остается постоянной и равной 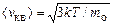. Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически выведен Дж. Максвеллом.Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Предполагалось также, что силовые поля на газ не действуют.

Закон Максвелла описывается некоторой функцией f(v), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные dv,то на каждый интервал скорости будет приходиться некоторое число молекул dN(v),имеющих скорость, заключенную в этом интервале. Функция f(v) определяет относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv,т. е. , откуда

.

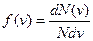Применяя методы теории вероятностей, Максвелл нашел функцию f(v) -закон для распределения молекул идеального газа по скоростям:

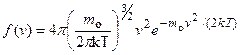
Из формулы видно, что конкретный вид функции зависит от рода газа (от массы молекулы) и от параметра состояния (от температуры Т).

График функции f(v) приведен на рис.65.

Так как при возрастании v множитель 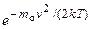уменьшается быстрее, чем растет множитель v²,то функция f(v), начинаясь от нуля, достигает максимума при и_в и затем асимптотически стремится к нулю. Кривая несимметрична относительно v_в.

Относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, находится как площадь более светлой полоски на рис.65. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Это означает, что функция f(v)удовлетворяет условию нормировки

.

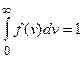Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью.Значение наиболее вероятной скорости можно найти, продифференцировав формулу Максвелла (постоянные множители опускаем) по аргументу v,приравняв результат нулю и используя условие для максимума выражения f(v):

.

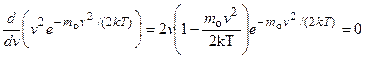Значения v=0и 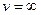соответствуют минимумам формулы, а значение v,при котором выражение в скобках становится равным нулю, и есть искомая наиболее вероятная скорость v_в:

.

Из полученной формулы следует, что при повышении температуры максимум функции распределения молекул по скоростям (рис.66) сместится вправо (значение наиболее вероятной скорости становится больше). Однако площадь, ограниченная кривой, остается неизменной, поэтому при повышении температуры кривая распределения молекул по скоростям будет растягиваться и понижаться.

Средняя скорость молекулы 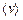(средняя арифметическая скорость)определяется по формуле

.

Подставляя сюда f(v)и интегрируя, получим

.

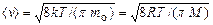Скорости, характеризующие состояние газа: 1) наиболее вероятная ;2)средняя 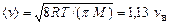; З) средняя квадратичная (рис.65).

Исходя из распределения молекул по скоростям

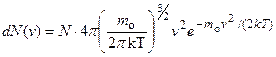
можно найти распределение молекул газа по значениям кинетической энергии Ɛ. Для этого перейдем от переменной v к переменной . Подстави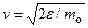в) в 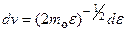, получим

,

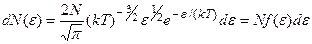где 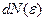- число молекул, имеющих кинетическую энергию поступательного движения, заключенную в интервале отƐдоƐ+dƐ.

Таким образом, функция распределения молекул по энергиям теплового движения

.

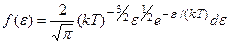Средняя кинетическая энергия 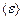молекулы идеального газа

,

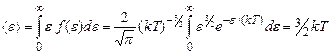т.е. получили результат, совпадающий с ранее выведенными формулами.

В состоянии термодинамического равновесия частицы физической системы движутся в основном со скоростями, близкими к скорости их теплового движения. Все частицы перемещаются с хаотически различными скоростями, движение каждой из которых подчиняется законам классической физики. Но для рассмотрения движения очень большого числа частиц используются статистические (вероятностные) законы физики.

Найдем функцию вероятности распределения молекул идеального газа по скоростям.

Задача заключается в том, чтобы найти вероятность dW(v) обнаружения частицы, значение скорости которой заключено в интервале (v; v+dv).

Мерой интервала является малый объем dV= dv_x dv_y dv_z в пространстве скоростей (v - пространство), в котором по координатным осям откладываются проекции скорости v_x, v_y, v_z. Следовательно,

где f(v) - плотность вероятности, или функция вероятности распределения молекул по скоростям.

В связи с тем, что в данный момент времени любая молекула имеет вполне определенное значение скорости, то должно выполняться условие нормировки, т.е. .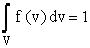

Если обозначим dN число молекул скорости которых лежат в интервале от v до v+dv, то вероятность dW(v) обнаружения частицы, значение скорости которой заключено в этом интервале равна dN/N. Отсюда получаем

Функция вероятности распределения молекул по скоростям

,

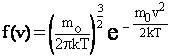(2.2)

где k - постоянная Больцмана, m₀ - масса одной молекулы; е - основание натуральных логарифмов (е=2,72).

Полученный результат справедлив не только для газа, но и любого тела, находящего в состоянии термодинамического равновесия, если движение его частиц подчиняется классическим законам, т.е. вид распределения не зависит от того, как взаимодействуют частицы между собой. Определяющим фактором здесь является способность частиц обмениваться энергией при переходе к равновесному состоянию.

Следовательно, вероятность обнаружить частицу с некоторой скоростью в пределах интервала (v; v+dv), c учетом (2.1), описывается функцией

.

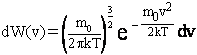(2.3)

Формула (2.3) выражает распределение Максвелла для скоростей молекул.

Его справедливость ограничена областью применения законов классической физики для теплового движения. Согласно (2.2), функция вероятности распределения зависит только от величины скорости. В рассматриваемой системе координат (v-пространство) интервал (v; v + dv) можно изобразить в виде сферического слоя (внутренний радиус - v, внешний - dv).

По предположению, толщина слоя интервала (v; v + dv) - мала.

Поэтому при суммировании вероятностей dW(v) в пределах сферического слоя функция распределения остается неизменной. Тогда суммарный объем всех элементарных объемов сферического слоя V=4v²dv.

Вывод: для тел, находящихся в состоянии термодинамического равновесия, вероятность dW(v) обнаружить частицу этого тела со скоростью движения, абсолютное значение которой заключено в интервале (v; v + dv),

.

(2.4)

Полученную формулу называют распределением Максвелла по абсолютным значениям скоростей, плотность вероятности которой

(v) = 4v²f(v)=dn/n₀dv

имеет вид

,

(2.5)

где dW(v) = (v)dv =dn/n₀ - вероятность того, что модуль скорости молекулы заключен в интервале (v; v+dv).

График зависимости (v) приведен на рис. 2.1. Справа представлена компьютерная модель распределения Максвелла.

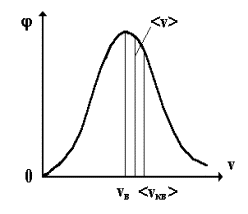Рис. 2.1

Компьютерная модель "Распределение Максвелла"

В сосуде, содержащем большое число молекул, устанавливается статистическое распределение молекул по скоростям, зависящее от абсолютной температуры – распределение Максвелла. Компьютерная модель предназначена для изучения равновесного распределения молекул по скоростям. На экран выводится кривая распределения при заданной температуре и вычисляются среднеквадратичная 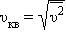и наиболее вероятная υ_в скорости. Можно изменять температуру газа T и наблюдать смещение максимума кривой распределения. Все молекулы, скорости которых попали в выделенный интервал, окрашиваются в зеленый цвет. Среднюю скорость молекул, попавших в выделенный интервал, можно изменять, перемещая интервал по оси скоростей. Можно качественно наблюдать за количеством и скоростью движения окрашенных молекул. Обратите внимание, что количество зеленых молекул максимально, когда выделенный интервал скоростей располагается вблизи максимума кривой распределения. Скорость таких молекул близка с наиболее вероятной скорости υ_в.

Величину скорости, при которой функция (v) максимальна, называют наиболее вероятной скоростью v_в.

Дифференцируя выражение (2.5) по аргументу v² и приравняв его нулю, получим

.

Из последнего выражения следует, что наиболее вероятная скорость

.

(2.6)

Максимум кривой на рис. 2.1 соответствует значению наиболее вероятной скорости v_в.

Из формулы (2.6) следует, что при увеличении температуры идеального газа (или уменьшении массы молекулы) максимум кривой смещается вправо и становится ниже при неизменной площади под кривой, а доля молекул, имеющие малые скорости, уменьшается, напротив - доля молекул с большими скоростями увеличивается. Это же можно пронаблюдать и на компьютерной модели "Распределение Максвелла". Для этого нажмите кнопку "Сброс" и меняя температуру Т наблюдайте смещение и изменение максимума кривой распределения(v).

Средняя арифметическая скорость молекул

или

.

Интегрируя последнее выражение с учетом (2.5), получаем

.

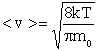(2.7)

Средняя квадратичная скорость - квадратный корень из среднего значения квадрата тепловой скорости поступательного движения молекулы

<v_кв> = ,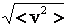

где .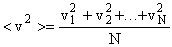

Давление, производимое молекулами при их тепловом хаотическом движении на стенки сосуда, в котором они находятся, рассчитывается по формуле:

.

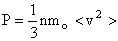Отсюда получаем

,

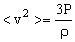где  =nm_o.

При постоянной температуре газа, применяя уравнение состояния идеального газа в виде 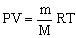или 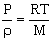, получаем

<vкв> = .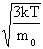

(2.8)

Средняя квадратичная скорость не имеет смысла для одной молекулы, а характеризует движение всей совокупности молекул.

При t=0⁰C средняя квадратичная скорость для азота - <v_кв> =493 м/c; для водорода - <v_кв>=1838 м/c; для кислорода -<v_кв> = 461 м/c.

Замечание: средняя квадратичная скорость такого же порядка, что и скорость звука в газе, так как передача возмущений в звуковой волне осуществляется молекулами, движущимися с тепловыми скоростями. Это же относится и к скорости истечения газа в вакуум.

Таким образом, все три скорости <v>, <v_кв> и v_в характеризуют тепловое движение молекул газа и различаются только числовыми коэффициентами

,

,

.

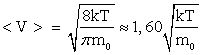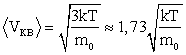Изучение вероятности распределения теплового движения молекул по скоростям (распределение Максвелла) осуществлялось различными экспериментальными методами (опыты Штерна, Ламмерта и др.).