Динамика материальной точки. Законы Ньютона. Понятие об инерциальной системе отсчета. Понятие о силе и массе. Взаимодействие в классической механике. Границы применимости классической механики.
Динамика изучает законы движения тел и причины, которые вызывают или изменяют это движение.
Как говорилось, динамикаизучает причины, которые вызывают именно такой характер движения, а не иной.
Динамика опирается на три закона Ньютона.
Законы Ньютона
Первый закон Ньютона. Если на тело не действуют силы или их действие скомпенсировано, то данное тело находится в состоянии покоя или равномерного прямолинейного движения.
Свойство тел сохранять свою скорость при отсутствии действия на него других тел называется инерцией.
Масса тела – количественная мера его инертности. В СИ она измеряется в килограммах.
Системы отсчета, в которых выполняется первый закон Ньютона, называются инерциальными. Системы отсчета, движущиеся относительно инерциальных с ускорением, называются неинерциальными.
Сила – количественная мера взаимодействия тел. Сила – векторная величина и измеряется в ньютонах (Н). Сила, которая производит на тело такое же действие, как несколько одновременно действующих сил, называется равнодействующей этих сил.
Второй закон Ньютона. Ускорение тела прямо пропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе:
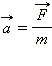 или или 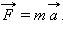
|
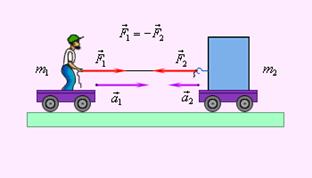
Если два тела взаимодействуют друг с другом, то ускорения этих тел обратно пропорциональны их массам.
|
| Рис. 1. Взаимодействие двух тел |
Третий закон Ньютона. Силы, с которыми тела взаимодействуют друг с другом, равны по модулю и направлены вдоль одной прямой в противоположные стороны.
ИНЕРЦИАЛЬНАЯ система ОТСЧЕТА - система отсчета, в которой справедлив закон инерции: материальная точка, на которую не действуют никакие силы, находится в состоянии покоя или равномерного прямолинейного движения.

Работа силы. Мощность. Кинетическая энергия. Теорема об изменении кинетической энергии. Примеры вычисления работы различных сил.
Работой, совершаемой постоянной силой F, называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла между векторами силы F и перемещения S:
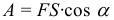
Работа является скалярной величиной. Она может быть как положительна (0° ≤ α < 90°), так и отрицательна (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 ньютон на перемещении 1 метр в направлении действия силы.
Если же сила изменяется с течением времени, то для нахождения работы строят график зависимости силы от перемещения и находят площадь фигуры под графиком – это и есть работа:
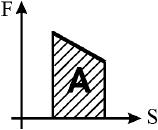
Примером силы, модуль которой зависит от координаты (перемещения), может служить сила упругости пружины, подчиняющаяся закону Гука (Fупр = kx).
Работа силы, совершаемая в единицу времени, называется мощностью. Мощность P (иногда обозначают буквой N) – физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:
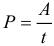
По этой формуле рассчитывается средняя мощность, т.е. мощность обобщенно характеризующая процесс. Итак, работу можно выражать и через мощность: A = Pt (если конечно известна мощность и время совершения работы). Единица мощности называется ватт (Вт) или 1 джоуль за 1 секунду. Если движение равномерное, то:
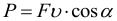
По этой формуле мы можем рассчитать мгновенную мощность (мощность в данный момент времени), если вместо скорости подставим в формулу значение мгновенной скорости. Как узнать, какую мощность считать? Если в задаче спрашивают мощность в момент времени или в какой-то точке пространства, то считается мгновенная. Если спрашивают про мощность за какой-то промежуток времени или участок пути, то ищите среднюю мощность.
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела (энергией движения):
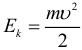
Физический смысл кинетической энергии: для того чтобы покоящееся тело массой m стало двигаться со скоростью v необходимо совершить работу равную полученному значению кинетической энергии. Если тело массой m движется со скоростью v, то для его остановки необходимо совершить работу равную его первоначальной кинетической энергии. При торможении кинетическая энергия в основном (кроме случаев соударения, когда энергия идет на деформации) «забирается» силой трения.
Теорема о кинетической энергии: работа равнодействующей силы равна изменению кинетической энергии тела:
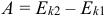
Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения. Применять данную теорему удобно в задачах на разгон и торможение тела.
Примеры, рассмотренные ниже, дают результаты, которыми можно пользоваться при решении задач.
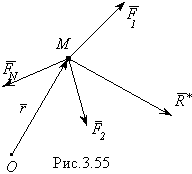 1. Работа равнодействующей силы. Теорема: Работа равнодействующей силы на некотором перемещении равна алгебраической сумме работ составляющих сил на том же перемещении.
1. Работа равнодействующей силы. Теорема: Работа равнодействующей силы на некотором перемещении равна алгебраической сумме работ составляющих сил на том же перемещении.
Допустим, что на точку действуют силы 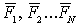 (рис.3.55)
(рис.3.55)
Равнодействующая этих сил 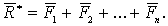
Если точка M получает элементарное перемещение 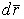 , то элементарная работа равнодействующей силы
, то элементарная работа равнодействующей силы 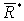 на этом перемещении
на этом перемещении
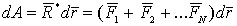 . Для вычисления работы равнодействующей силы на участке
. Для вычисления работы равнодействующей силы на участке 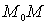 воспользуемся формулой (3.103)
воспользуемся формулой (3.103)
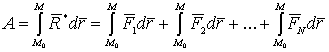 , или
, или
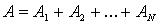 . (3.106)
. (3.106)
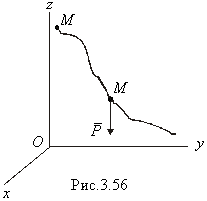 2. Работа силы тяжести. Найдем сначала работу силы тяжести для точки. Пусть точка, на которую действует сила тяжести
2. Работа силы тяжести. Найдем сначала работу силы тяжести для точки. Пусть точка, на которую действует сила тяжести 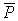 перемещается из положения
перемещается из положения 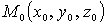 в положение
в положение 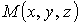 . Выберем оси координат так, чтобы ось z была направлена вертикально вверх (рис.3.56).
. Выберем оси координат так, чтобы ось z была направлена вертикально вверх (рис.3.56).
В этом случае 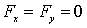 ,
, 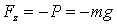 .
. 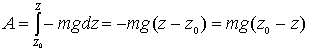 .
.
Обозначим 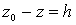 , где h - величина вертикального перемещения точки. Если точка
, где h - величина вертикального перемещения точки. Если точка 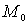 выше
выше 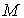 , то
, то 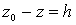 , если же точка
, если же точка 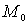 ниже
ниже 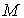 , то
, то 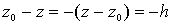 . Поэтому
. Поэтому
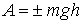 , (3.107)
, (3.107)
т.е. работа силы тяжести равна взятому со знаком плюс или минус произведению силы тяжести на вертикальное перемещение точки ее приложения. Работа положительна, если точка опускается, и отрицательна, если точка поднимается.
Для механической системы работа силы тяжести K-ой точки будет 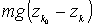 . Тогда сумма работ всех сил тяжести, действующих на систему:
. Тогда сумма работ всех сил тяжести, действующих на систему:
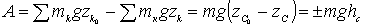 , (3.108)
, (3.108)
где mg - сила тяжести системы, 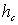 - вертикальное перемещение центра масс системы.
- вертикальное перемещение центра масс системы.
6. Консервативные и неконсервативные силы. Потенциальная энергия.
Силы, действующие на тело, могут быть консервативными и неконсервативными. Сила называется консервативной или потенциальной, если работа, совершаемая этой силой при перемещении материальной точки из одного положения в другое, не зависит от вида траектории (формы пути) и определяется только начальным и конечным положениями тела (рис.3.1): А1В2 = А1С2 = А12.
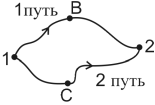
Рис.3.1
В случае, если тело движется в обратном направлении А12= –А21, т.е. изменение направления движения по траектории на противоположное вызывает изменение знака работы. Следовательно, при движении материальной точки по замкнутой траектории работа консервативной силы равна нулю (например, поднятие и опускание груза):
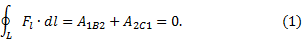
Консервативными силами являются силы гравитационного взаимодействия, силы упругости, электростатические силы. Силы, не удовлетворяющие условию (1), называются неконсервативными. К неконсервативным силам относят силы трения и сопротивления. Поле, в котором действуют консервативные силы, называется потенциальным.
Конечно, помимо консервативных сил есть неконсервативные. Это все остальные силы, чья работа вычисляется по пути.
Неконсервативные силы:
Сила трения
Сила трения возникает при движении одного тела по поверхности другого и равна:
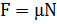
μ - коэффициент трения,
N - сила реакции опоры.
Коэффициент трения зависит от материала тел, состояния их поверхности и т. д., но он не зависит от площади трущихся тел.
Сила сопротивления воздуха
Сила сопротивления воздуха возникает, когда тело какой-то формы движется со скоростью V в воздухе. Для некоторого диапазона скоростей эта сила пропорциональна квадрату скорости:
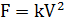
k - коэффициент пропорциональности, зависящий от формы движущегося тела и его прочих характеристик.
Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями (так называемые консервативные силы). Работа таких сил на замкнутой траектории равна нулю. Таким свойством обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.
Потенциальная энергия тела в поле силы тяжести Земли рассчитывается по формуле:
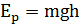
Физический смысл потенциальной энергии тела: потенциальная энергия равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень (h – расстояние от центра тяжести тела до нулевого уровня). Если тело обладает потенциальной энергией, значит оно способно совершить работу при падении этого тела с высоты h до нулевого уровня. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:
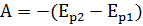
Рис.1
Если изобразить последнее колебание вектором длины 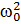 a, направленным вправо, то колебание изобразится вектором длины
a, направленным вправо, то колебание изобразится вектором длины 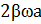 , повернутым относительно вектора
, повернутым относительно вектора 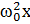 против часовой стрелки на угол
против часовой стрелки на угол  , а колебание (6) – вектором длины
, а колебание (6) – вектором длины 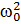 a, повернутым относительно вектора
a, повернутым относительно вектора 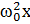 на угол
на угол 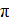 . Чтобы уравнение (2) было удовлетворено, векторная сумма перечисленных трех векторов должна совпадать с вектором, изображающим колебание
. Чтобы уравнение (2) было удовлетворено, векторная сумма перечисленных трех векторов должна совпадать с вектором, изображающим колебание  . Такое совпадение возможно лишь при значении амплитуды а, которое определяется условием рис 1. (а)
. Такое совпадение возможно лишь при значении амплитуды а, которое определяется условием рис 1. (а)
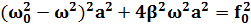
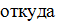
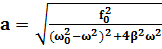 (7)
(7)
Рис1. (а) отвечает случаю 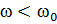 . Из рис.1.(б) соответствующего случаю
. Из рис.1.(б) соответствующего случаю  , получается такое же значение а.
, получается такое же значение а.
Рис1. Позволяет получить также и значение  , которое представляет собой величину отставания по фазе вынужденного колебания (4) от обусловившей его вынуждающей силы (1). Из рисунка следует, что
, которое представляет собой величину отставания по фазе вынужденного колебания (4) от обусловившей его вынуждающей силы (1). Из рисунка следует, что
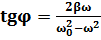 (8)
(8)
Подставив в (4) значение а и  , определяемые формулами (5) и (6), получим частное решение неоднородного уравнения (4) :
, определяемые формулами (5) и (6), получим частное решение неоднородного уравнения (4) :
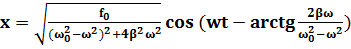 (9)
(9)
Функция (9) в сумме с (3) дает общее решение уравнения (2), описывающее поведение системы при вынужденных колебаниях. Функция (9) описывает установившиеся вынужденные колебания. Они представляют собой гармонические колебания с частотой, равной частоте вынуждающей силы. Амплитуда (7) вынужденных колебаний пропорциональна амплитуде вынуждающей силы. Для данной колебательной системы (определенных 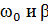 ) ампилтуда зависит от частоты вынуждающей силы. Вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания
) ампилтуда зависит от частоты вынуждающей силы. Вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания  также зависит от частоты вынуждающей силы.
также зависит от частоты вынуждающей силы.
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Колебательная система оказывается особенно отзывчивой на действие вынуждающей силы при этой частоте. Это явление называется резонансом, а соответствующая частота – резонансной частотой.
С явлением резонанса приходится считаться при конструировании машин и различного рода сооружений. Собственная частота колебаний этих устройств ни в коем случае не должна быть близка к частоте возможных внешних воздействий. Так, например, собственная частота вибраций корпуса корабля или крыльев самолета должна сильно отличаться от частоты колебаний, которые могут быть возбуждены вращением гребного винта или пропеллера. В противном случае возникают вибрации, которые могут вызвать катастрофу.
Основные положения молекулярно-кинетической теории строения вещества. Основное уравнение молекулярно-кинетической теории газов. Давление газов. Уравнение Менделеева – Клапейрона. Температура. Способы построения температурных шкал.
Молекулярно-кинетической теорией (МКТ) называют учение о строении и свойствах вещества на основе представления о существовании атомов и молекул как наименьших частиц химических веществ.
В основе молекулярно-кинетической теории лежат три основных положения:
1. Все вещества – жидкие, твердые и газообразные – образованы из мельчайших частиц – молекул, которые сами состоят из атомов («элементарных молекул»). Молекулы химического вещества могут быть простыми и сложными, т.е. состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы.
2. Атомы и молекулы находятся в непрерывном хаотическом движении. (доказательством является броуновское движение)
3. Частицы взаимодействуют друг с другом силами, имеющими электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало.
Температура.
Если несколько соприкасающихся тел находятся в состоянии теплового равновесия, т.е. не обмениваются энергией путем теплопередачи, то этим телам приписывается одинаковая температура. Если при установлении теплового контакта между телами одно из них передает энергию другому посредством теплопередачи, то первому телу приписывается большая температура, чем второму. Ряд свойств тел- объем, электрическое сопротивление и т.п. - зависит от температуры. Любое из этих свойств может быть использовано для количественного определения температуры.
Приведем тело, в тепловое равновесие с тающим льдом, припишем телу в этом случае температуру 0 и охарактеризуем количественно то свойство тела (температурный признак), которое мы намереваемся использовать для измерения температуры. Пусть в качестве такого признака выбран объем тела и значение его при 0 равно 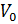 . Затем приведем то же тело в тепловое равновесие с кипящей под атмосферным давлением водой,припишем ему в этом состоянии значение температуры, равное
. Затем приведем то же тело в тепловое равновесие с кипящей под атмосферным давлением водой,припишем ему в этом состоянии значение температуры, равное 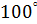 , и определим соответствующий объем
, и определим соответствующий объем 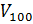 . Принимая, что выбранный нами температурный признак (объем) изменяется с температурой линейно, состоянию, в котором термометрическое тело имеет объем V, следует приписать температуру
. Принимая, что выбранный нами температурный признак (объем) изменяется с температурой линейно, состоянию, в котором термометрическое тело имеет объем V, следует приписать температуру
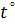 =
= 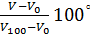
Установленная таким образом температурная шкала называется, как известно, шкалой Цельсия.
Температурные шкалы - способы деления на части интервалов температуры, измеряемых термометрами по изменению какого-либо удобного для измерений физического свойства объекта, при прочих равных условиях однозначно зависящего от температуры (объёма, давления, электрического сопротивления, ЭДС, интенсивности излучения, показателя преломления, скорости звука и др.) и называемого термометрическим свойством (см. Термометрия). Для построения шкалы температур приписывают её численные значения двум фиксированным точкам (реперным точкам температуры), например точке плавления льда и точке кипения воды. Деля разность температур реперных точек (основной температурный интервал) на выбранное произвольным образом число частей, получают единицу измерения температуры, а задавая, опять-таки произвольно, функциональную связь между выбранным термометрическим свойством и температурой, получают возможность вычислять температуру по данной температурной шкале[1].
Шкала Кельвина
В термодинамике используется шкала Кельвина, в которой температура отсчитывается от абсолютного нуля (состояние, соответствующее минимальной теоретически возможной внутренней энергии тела), а один кельвин равен 1/273.16 расстояния от абсолютного нуля до тройной точки воды (состояния, при котором лёд, вода и водяной пар находятся в равновесии). Для пересчета кельвинов в энергетические единицы служит постоянная Больцмана. Используются также производные единицы: килокельвин, мегакельвин, милликельвин и т.д.
Шкала Цельсия
В быту используется шкала Цельсия, в которой за 0 принимают точку замерзания воды, а за 100° точку кипения воды при атмосферном давлении. Поскольку температура замерзания и кипения воды недостаточно хорошо определена, в настоящее время шкалу Цельсия определяют через шкалу Кельвина: градус Цельсия равен кельвину, абсолютный ноль принимается за −273,15 °C. Шкала Цельсия практически очень удобна, поскольку вода очень распространена на нашей планете и на ней основана наша жизнь. Ноль Цельсия — особая точка для метеорологии, поскольку замерзание атмосферной воды существенно всё меняет.
Шкала Фаренгейта
В Англии и, в особенности, в США используется шкала Фаренгейта. В этой шкале на 100 градусов раздёлен интервал от температуры самой холодной зимы в городе, где жил Фаренгейт, до температуры человеческого тела. Ноль градусов Цельсия — это 32 градуса Фаренгейта, а градус Фаренгейта равен 5/9 градуса Цельсия.
В настоящее время принято следующее определение шкалы Фаренгейта: это температурная шкала, 1 градус которой (1 °F) равен 1/180 разности температур кипения воды и таяния льда при атмосферном давлении, а точка таяния льда имеет температуру +32 °F. Температура по шкале Фаренгейта связана с температурой по шкале Цельсия (t °С) соотношением t °С = 5/9 (t °F - 32), то есть изменение температуры на 1 °F соответствует изменению на 5/9 °С. Предложена Г. Фаренгейтом в 1724.
Шкала Реомюра
Предложенна в 1730 году Р. А. Реомюром, который описал изобретённый им спиртовой термометр.
Единица — градус Реомюра (°R), 1 °R равен 1/80 части температурного интервала между опорными точками — температурой таяния льда (0 °R) и кипения воды (80 °R)
1 °R = 1,25 °C.
В настоящее время шкала вышла из употребления, дольше всего она сохранялась во Франции, на родине автора.
Второй закон термодинамики.
Процессы в природе необратимы, а их направление подчиняется общей закономерности – более упорядоченные состояния замкнутых систем переходят в менее упорядоченные.
Тепловые машины . 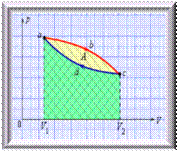
Реально существующие тепловые машины работают циклически. При расширении газ совершает положительную работу A1, равную площади под кривой abc, при сжатии газ совершает отрицательную работу A2, равную по модулю площади под кривой cda. Полная работа за цикл на диаграмме (p, V) равна площади фигуры, ограниченной графиками цикла.
Принцип работы тепловой машины. Тепловой машиной называется устройство, в котором внутренняя энергия превращается в механическую.
• 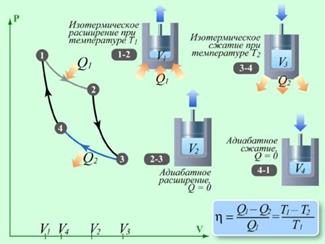
Сади Карно, анализируя идеальный круговой процесс (известный сейчас как цикл Карно), впервые пришёл к выводу о том, что полезная работа производится только при переходе тепла от нагретого тела к холодному. На участке (1–2) газ изотермически расширяется, совершая работу A12, при этом к газу подводится некоторое количество теплоты Q1 = A12. На участке (2–3) газ продолжает адиабатно расширяться в отсутствие теплообмена, совершая работу A23 > 0. Температура газа падает до T2. На участке (3–4) газ приводится в тепловой контакт с холодильником при температуре T2 < T1. Происходит процесс изотермического сжатия. Газ совершает работу A34 < 0 и отдает тепло Q2 < 0, Q2 = A34,холодильнику . Внутренняя энергия газа не изменяется. На участке (3-4) адиабатического сжатия температура газа повышается до T1, газ совершает работу A41 < 0. Полная работа A, совершаемая газом за цикл, равна сумме работ на отдельных участках:
• 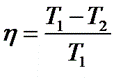 A = A12 + A23 + A34 + A41. На диаграмме (p, V) эта работа равна площади цикла.
A = A12 + A23 + A34 + A41. На диаграмме (p, V) эта работа равна площади цикла.
коэффициент полезного действия цикла Карно.
Рабочее тело, получая некоторое количество теплоты Q1от нагревателя, часть этого количества теплоты, по модулю равную |Q2|,отдает холодильнику. Поэтому совершаемая работа не может быть больше A = Q1 — |Q2|.
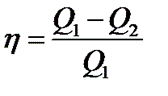
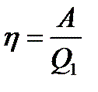 Отношение этой работы к количеству теплоты, полученному расширяющимся газом от нагревателя, называется коэффициентом полезного действия тепловой машины:
Отношение этой работы к количеству теплоты, полученному расширяющимся газом от нагревателя, называется коэффициентом полезного действия тепловой машины:
• Q1 > Q2 , A > 0; T1 > T2.
Второй закон термодинамики по Клаузиусу: невозможен круговой процесс, единственнымрезультатом которого является передача теплоты от менее нагретого тела к более нагретому. вечный двигатель второго рода;
• В циклически действующей тепловой машине невозможен круговой процесс, единственным
результатом которого было бы преобразование в механическую работу всего количества теплоты, полученного от единственного нагревателя ( невозможен вечный двигатель второго рода ). Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.
• Второе начало термодинамики гласит, что невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому.
• Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая невозможность перехода всей внутренней энергии системы в полезную работу.
• Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения.
• Примеры тепловых машин: двигатель внутреннего сгорания (ДВС): а)карбюраторный двигатель, б) дизельный двигатель, в) реактивный двигатель. Паровые и газовые турбины.
• КПД
• Карбюраторный двигатель 25%
• Дизельный двигатель 38%
Реактивный двигатель 30%
• Паровая турбина 25%
• Газовая турбина 55%
Формулировка Планка для третьего начала термодинамики
В 1911 году М. Планк сформулировал третье начало термодинамики, при котором энтропия всех тел обращается в ноль, когда температура стремиться к нулевому значению.
Это позволяет определять абсолютные значения энтропии и остальных термодинамических потенциалов. Формулировка Планка является соответствием определению энтропии в статистической физике с помощью термодинамической вероятности состояния системы:
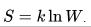
Рисунок 3. Формулировка Планка.
Система (при абсолютном нуле температуры) пребывает в базовом квантово-механическом состоянии. Если оно не вырождено, энтропия равна нулю и состояние реализуется единственно возможным микрораспределением.
На самом деле, стремление энтропии к нулю при всех измерениях начинает проявляться гораздо раньше, чем могут стать существенными воздействие квантового вырождения и дискретность квант-уровней макроскопической системы.
Согласно третьему началу термодинамики, достичь абсолютного нуля температуры нельзя ни в каком конечном процессе, имеющим отношение к изменению энтропии. К нему возможно приблизиться только асимптотически. По этой причине третье начало термодинамики иногда формулируются в виде принципа недостижимости абсолютного нуля температур.
Нарушения третьего начала термодинамики Из третьего начала термодинамики вытекают определенные термодинамические следствия: при
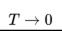
должны будут стремиться к нулевому значению теплоемкости (при постоянном давлении и объеме), а также коэффициенты теплового расширения и некоторые из аналогичных величин.
Некоторое время справедливость 3-го начала термодинамики подвергалась сомнению, однако позднее ученым удалось выяснить, что все изначально кажущиеся противоречия (ненулевое значение энтропии для ряда веществ) при
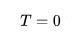
взаимосвязаны с метастабильными состояниями вещества, которые не считаются термодинамически равновесными).
Третье начало термодинамики зачастую нарушается в модельных системах. Так, при
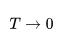
энтропия у классического идеального газа будет стремиться к минус бесконечности. Это означает, что уравнение Менделеева-Клапейрона при низких температурах некорректно описывает поведение реальных газов.
Третье начало термодинамики, таким образом, демонстрирует недостаточность статистики и классической механики и служит макроскопическим проявлением квантовых качеств в отношении реальных систем.
В модельных системах (в квантовой механике) третье начало может быть нарушено. Это могут быть случаи применения распределения Гиббса.
В то же время несоблюдение 3-го начала в модели не исключает, что в каком-то отдельном диапазоне изменения физических величин данная модель может быть вполне адекватной.
Закон Кулона
Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь. На основании многочисленных опытов Кулон установил следующий закон:
Силы взаимодействия неподвижных точечных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:
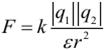
где: ε – диэлектрическая проницаемость среды – безразмерная физическая величина, показывающая, во сколько раз сила электростатического взаимодействия в данной среде будет меньше, чем в вакууме (то есть во сколько раз среда ослабляет взаимодействие). Здесь k – коэффициент в законе Кулона, величина, определяющая численное значение силы взаимодействия зарядов. В системе СИ его значение принимается равным:
k = 9∙109 м/Ф.
Силы взаимодействия точечных неподвижных зарядов подчиняются третьему закону Ньютона, и являются силами отталкивания друг от друга при одинаковых знаках зарядов и силами притяжения друг к другу при разных знаках. Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой.
Закон Кулона справедлив для точечных заряженных тел, равномерно заряженных сфер и шаров. В этом случае за расстояния r берут расстояние между центрами сфер или шаров. На практике закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними. Коэффициент k в системе СИ иногда записывают в виде:
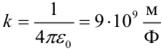
где: ε0 = 8,85∙10–12 Ф/м – электрическая постоянная.
Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции: если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.
Принцип суперпозиции
Если с помощью пробного заряда исследуется электрическое поле, создаваемое несколькими заряженными телами, то результирующая сила оказывается равной геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряжённостей электрических полей, создаваемых в той же точке зарядами в отдельности:

Это свойство электрического поля означает, что поле подчиняется принципу суперпозиции. В соответствии с законом Кулона, напряженность электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю:
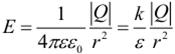
Это поле называется кулоновским. В кулоновском поле направление вектора напряженности зависит от знака заряда Q: если Q > 0, то вектор напряженности направлен от заряда, если Q < 0, то вектор напряженности направлен к заряду. Величина напряжённости зависит от величины заряда, среды, в которой находится заряд, и уменьшается с увеличением расстояния.
Напряженность электрического поля, которую создает заряженная плоскость вблизи своей поверхности:
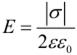
Итак, если в задаче требуется определить напряженность поля системы зарядов, то надо действовать по следующему алгоритму:
1. Нарисовать рисунок.
2. Изобразить напряженность поля каждого заряда по отдельности в нужной точке. Помните, что напряженность направлена к отрицательному заряду и от положительного заряда.
3. Вычислить каждую из напряжённостей по соответствующей формуле.
4. Сложить вектора напряжённостей геометрически (т.е. векторно).
17. Теорема Остроградского - Гаусса и ее применения для расчета напряженности электростатических полей (поле плоскости, нити, сферы, шара).
К.Ф. Гаусс (1777–1855) выдающийся немецкий математик, астроном и физик в 1839г. предложил теорему, которая устанавливает связь потока вектора напряженности электрического поля через  замкнутую поверхность со значением заряда q, находящегося внутри этой поверхности. Эта теорема выведена математически для векторного поля любой природы русским математиком М.В. Остроградским (1801-1862), а затем независимо от него применительно к электростатическому полю – К.Гауссом.
замкнутую поверхность со значением заряда q, находящегося внутри этой поверхности. Эта теорема выведена математически для векторного поля любой природы русским математиком М.В. Остроградским (1801-1862), а затем независимо от него применительно к электростатическому полю – К.Гауссом.
Теорема Остроградского – Гаусса (теорема Гаусса): поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на 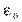 :
:
 .
.
Применение теоремы Гаусса к расчету электрических полей
Использование теоремы Гаусса для расчета полей эффективно в тех случаях, когда поле обладает специальной симметрией (чаще всего плоской, цилиндрической или сферической). Симметрия и конфигурация поля должны быть такими, чтобы, во-первых, заряженное тело можно было бы окружить достаточно простой замкнутой поверхностью и, во-вторых, вычисление потока вектора напряженности свести к простому умножению Е (или En) на площадь поверхности S или часть ее. Если этого сделать нельзя, то задачу необходимо решать другими методами.
Магнитное действие тока. Магнитостатика вакуума. Элемент тока. Закон Био-Савара–Лапласа и его применение для расчета напряженности магнитного поля прямого бесконечного проводника с током, кольца с током.
Магнитное действие электрического тока
При наличии электрического тока в любом проводнике (в твердом, жидком или газообразном) наблюдается магнитное поле вокруг проводника, то есть проводник с током приобретает магнитные свойства.
Так, если к проводнику, по которому течет ток, поднести магнит, например в виде магнитной стрелки компаса, то стрелка повернется перпендикулярно проводнику, а если намотать проводник на железный сердечник, и пропустить по проводнику постоянный ток, то сердечник станет электромагнитом.
В 1820 году Эрстед открыл магнитное действие тока на магнитную стрелку, а Ампер установил количественные закономерности магнитного взаимодействия проводников с током.
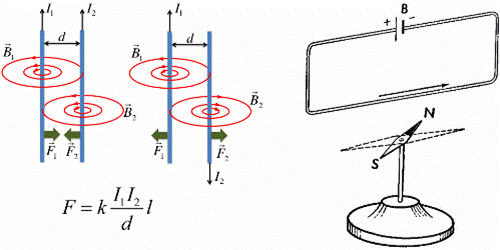
Магнитное поле всегда порождается током, то есть движущимися электрическими зарядами, в частности - заряженными частицами (электронами, ионами). Противоположно направленные токи взаимно отталкиваются, однонаправленные токи взаимно притягиваются.
Такое механическое взаимодействие происходит благодаря взаимодействию магнитных полей токов, то есть это, в первую очередь, - магнитное взаимодействие, а уж потом - механическое. Таким образом, магнитное взаимодействие токов первично.
Элемент (электрического) тока векторная величина, равная произведению электрического токапроводимости вдоль линейного проводника и бесконечно малого отрезка этого проводника
Закон Био–Савара. Теорема о циркуляции Магнитное поле постоянных токов различной конфигурации изучалось экспериментально французскими учеными Ж. Био и Ф. Саваром (1820 г.). ... Закон Био–Савара определяет вклад в магнитную индукцию результирующего магнитного поля, создаваемый малым участком Δl проводника с током
Закон Фарадея
 |
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из N витков, то ЭДС индукции:

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением R:

При движении проводника длиной l со скоростью v в постоянном однородном магнитном поле с индукцией B⃗ ЭДС электромагнитной индукции равна:
где α – угол между векторами B⃗ и v⃗ .
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
29. Переменный электрический ток. Получение переменного тока. Действующее значение тока и напряжения. Индуктивность и емкость в цепи переменного тока. Закон Ома для переменного тока.
Переменный электрический ток — ток имеющий форму гармонического синусоидального сигнала, основными характеристиками которого являются действующее напряжение и частота, с течением времени изменяется по направлению и величине
Переменный ток, как и постоянный, также является упорядоченным движением заряженных частиц. Но постоянный ток всегда имеет одно направление, от «+» к «-». А переменный ток своё направление постоянно меняет, то есть течёт то в одну, то в другую сторону. Поэтому одно из его направлений условно принимают за положительное, а направление, противоположное ему, считают отрицательным. В зависимости от этого в конкретный момент времени алгебраическая величина тока будет иметь знак «плюс» или знак «минус».
Чтобы ток был переменным, он должен быть подключен к источнику переменной ЭДС. Такими источниками являются генераторы переменного тока – электрические машины, которые преобразуют механическую энергию в электрическую энергию тока.
Второе уравнение Максвелла
Второе уравнение Максвелла представляет собой ни что иное, как закон Фарадея. Его вид:
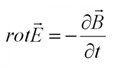
Ротор электрического поля (интеграл через замкнутую поверхность) равен скорости изменения магнитного потока, пронизывающего эту поверхность. Чтобы лучше понять, возьмем воду в ванной, которая сливается через отверстие. Вокруг отверстия образуется воронка. Ротор – это сумма (интеграл) векторов скоростей частиц воды, которые вращаются вокруг отверстия.
Как Вы помните, на основе закона Фарадея работают электродвигатели: вращающийся магнит порождает ток в катушке.
Третье уравнение Максвелла
третье уравнение Максвелла – это тоже закон Гаусса, только уже не для электрического поля, но для магнитного.
Оно имеет вид:
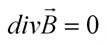
Что это значит? Поток магнитного поля через замкнутую поверхность равен нулю. Если электрические заряды (положительные и отрицательные) вполне могут существовать по отдельности, порождая вокруг себя электрическое поле, то магнитных зарядов в природе просто не существует.
Полное отражение
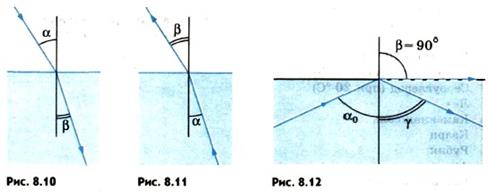
При прохождении света из оптически менее плотной среды в более плотную, например из воздуха в стекло или воду, υ1 > υ2 и, следовательно, согласно закону преломления показатель преломления n > 1. Поэтому α > β (рис. 8.10): в результате преломления луч приближается к нормали к границе раздела сред.
Если же направить луч света в обратном направлении — из оптически более плотной среды в оптически менее плотную вдоль ранее преломленного луча (рис. 8.11), то закон преломления можно записать так:

переломленный луч по выходе из оптически более плотной среды будет направлен по линии ранее падавшего луча, поэтому α < β, т. е. преломленный луч отклоняется на сей раз от нормали. По мере увеличения угла α угол преломления β также увеличивается, оставаясь все время больше угла α. Наконец, при некотором угле падения а значение угла преломления β приблизится к 90°, и преломленный луч будет направлен почти по границе раздела двух сред (рис. 8.12). Наибольшему возможному углу преломления β = 90° соответствует угол падения α0. При α > α0 преломление света невозможно. Значит, луч должен полностью отразиться. Это явление и называется полным отражением света.
Зеркало – это гладкая поверхность, которая отражает излучение. Оптические зеркала – это обычно полированные металлы или стекла, которые отражают почти весь видимый свет. Зеркала бывают трех видов – плоские, вогнуты и выпуклые.
Плоские зеркала отражают излучения без искажений и дают изображение, близкое к оригиналу (рис. 1).

Вогнутые – концентрируют энергию излучения (рис. 2).

Выпуклые – рассеивают (рис. 3).
ЛИНЗЫ
Линза — прозрачное тело, ограниченное двумя сферическими или сферической и плоской поверхностями, способное формировать оптическое изображение предмета.
Тонкая линза — линза, толщина которой пренебрежимо мала по сравнению с радиусами и Я2 кривизны поверхностей (рис. 6.8), ограничивающих линзу.
Разновидности тонких линз по форме (рис. 6.9): 1 —двояковыпуклая; 2 — плосковыпуклая; 3 — двояковогнутая; 4 — выпукловогнутая; 5 — вогнутовыпуклая; 6 — плосковогнутая. 1)рис
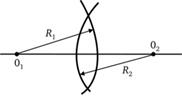
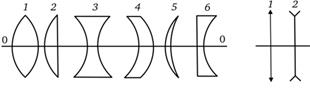 рис 6.9,6.10
рис 6.9,6.10
Линзы, преобразующие падающие на них параллельные лучи в сходящиеся, называются собирающими, а в расходящиеся — рассеивающими. На рис. 6.10 приведены условные обозначения линз: 1 — собирающая линза; 2 — рассеивающая линза.
Главная оптическая ось — прямая, проходящая через центры 0а и 02 кривизны обеих поверхностей линзы.
Главный оптический центр линзы — точка 0, лежащая на главной оптической оси, через которую лучи проходят, не изменяя своего направления (рис. 6.11).
Оптическая ось — любая прямая, проходящая через оптический центр линзы.
Побочная оптическая ось — любая прямая, проходящая через оптический центр линзы и не совпадающая с главной оптической осью.
Параксиальные (приосевые) лучи — лучи, составляющие небольшие углы с главной оптической осью.
Главный фокус линзы (F) — точка на главной оптической оси, в которой пересекаются лучи параксиального светового пучка, распространяющиеся параллельно главной оптической оси линзы. Линза имеет два главных фокуса, которые расположены по обе стороны от нее на фокусном расстоянии F от оптического центра линзы (рис. 6.11). Для собирающей линзы фокусы действительные, а рассеивающей — мнимые (рис. 6.11).
Фокальные плоскости — плоскости, проходящие через фокусы линзы перпендикулярно ее главной оптической оси.
Побочный фокус линзы (F') — точка пересечения побочной оптической оси с фокальными плоскостями линзы. В побочном фокусе сходятся все лучи, падающие на линзу параллельно любой оптической оси (рис. 6.12).
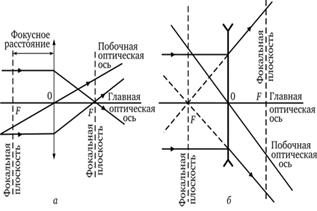
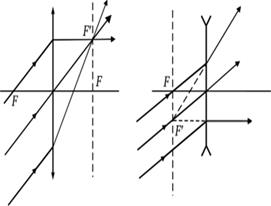
рис 6.11,6.12
Фокусное расстояние линзы — расстояние между оптическим центром линзы и ее фокусами.
Оптическая сила линзы — величина, обратная фокусному расстоянию:
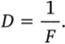
Единица оптической силы: диоптрий (1 дптр = 1м-1). Оптическая сила собирающей линзы положительна (?> > 0), рассеивающей— отрицательна (D < 0).
Оптическая сила линзы с радиусами поверхностей Ях и К2:
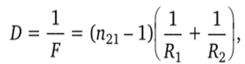 где n2i = п2/п2; пх и п2 — абсолютные показатели преломления материала линзы и окружающей среды.
где n2i = п2/п2; пх и п2 — абсолютные показатели преломления материала линзы и окружающей среды.
Правило расстановки знаков: если фокус, предмет и изображение являются действительными, то перед соответствующими членами ставится «плюс», если мнимые, то «минус». Если на линзу падает сходящийся пучок света, т. е. в случае мнимой светящейся точки, расстояние d берется со знаком «минус», а для действительной светящейся точки со знаком «плюс».
Оптическая сила системы линз равна сумме оптических сил линз, входящих в систему:
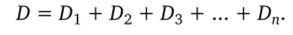
Закон Стефана-Больцмана.
Чтобы понять, как действует этот закон, представьте себе атом, излучающий свет в недрах Солнца. Свет тут же поглощается другим атомом, излучается им повторно — и таким образом передается по цепочке от атома к атому, благодаря чему вся система находится в состоянии энергетического равновесия. В равновесном состоянии свет строго определенной частоты поглощается одним атомом в одном месте одновременно с испусканием света той же частоты другим атомом в другом месте. В результате интенсивность света каждой длины волны спектра остается неизменной.
Температура внутри Солнца падает по мере удаления от его центра. Поэтому, по мере движения по направлению к поверхности, спектр светового излучения оказывается соответствующим более высоким температурам, чем температура окружающий среды. В результате, при повторном излучении, согласно закону Стефана—Больцмана, оно будет происходить на более низких энергиях и частотах, но при этом, в силу закона сохранения энергии, будет излучаться большее число фотонов. Таким образом, к моменту достижения им поверхности спектральное распределение будет соответствовать температуре поверхности Солнца (около 5 800 К), а не температуре в центре Солнца (около 15 000 000 К).
Энергия, поступившая к поверхности Солнца (или к поверхности любого горячего объекта), покидает его в виде излучения. Закон Стефана—Больцмана как раз и говорит нам, какова излученная энергия. Этот закон записывается так:
E = σT 4
где Т — температура (в кельвинах), а σ — постоянная Больцмана. Из формулы видно, что при повышении температуры светимость тела не просто возрастает — она возрастает в значительно большей степени. Увеличьте температуру вдвое, и светимость возрастет в 16 раз!
Первый закон излучения Вина
В 1893 году Вильгельм Вин, воспользовавшись, помимо классической термодинамики, электромагнитной теорией света, вывел следующую формулу:
· {\displaystyle u_{\nu }=\nu ^{3}f\left({\frac {\nu }{T}}\right),} 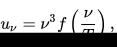
где uν — плотность энергии излучения, ν — частота излучения, T —температура излучающего тела, f — функция, зависящая только от отношения частоты к температуре.
Вид этой функции невозможно установить, исходя только из термодинамических соображений.
Первая формула Вина справедлива для всех частот. Любая более конкретная формула (например, закон Планка) должна удовлетворять первой формуле Вина.
Из первой формулы Вина можно вывести закон смещения Вина (закон максимума) и закон Стефана — Больцмана, но нельзя найти значения постоянных, входящих в эти законы.
Исторически именно первый закон Вина назывался законом смещения, но в настоящее время термином «закон смещения Вина» называют закон максимума.
Второй закон излучения Вина
В 1896 году Вин на основе дополнительных предположений вывел второй закон:
{\displaystyle u_{\nu }=C_{1}\nu ^{3}e^{-C_{2}{\frac {\nu }{T}}},} 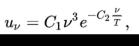
где C1, C2 — константы. Опыт показывает, что вторая формула Вина справедлива лишь в пределе высоких частот (малых длин волн). Она является частным конкретным случаем первого закона Вина.
Позже Макс Планк показал, что второй закон Вина следует из закона Планка для больших энергий квантов, а также нашёл постоянные C1 и C2. С учётом этого, второй закон Вина можно записать в виде:
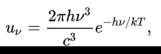 {\displaystyle u_{\nu }={\frac {2\pi h\nu ^{3}}{c^{3}}}e^{-h\nu /kT},}
{\displaystyle u_{\nu }={\frac {2\pi h\nu ^{3}}{c^{3}}}e^{-h\nu /kT},}
где h — постоянная Планка, k — постоянная Больцмана, c — скорость света в вакууме.
{\displaystyle R={\frac {U}{I}},}
Кинематика вращательного движения тела вокруг неподвижной оси. Связь линейных и угловых характеристик. Векторы угла поворота, угловой скорости и углового ускорения.
Движение твердого тела, при котором две его точки О и О' остаются неподвижными, называется вращательным движением вокруг неподвижной оси, а неподвижную прямую ОО' называют осью вращения.
Пусть абсолютно твердое тело вращается вокруг неподвижной оси ОО' (рис. 2.12).
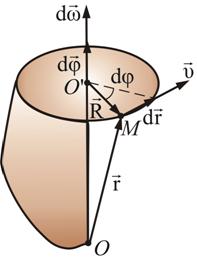
Проследим за некоторой точкой М этого твердого тела. За время dt точка М совершает элементарное перемещение dr.
При том же самом угле поворота dφ, другая точка, отстоящая от оси на большее или меньшее расстояние, совершает другое перемещение. Следовательно, ни само перемещение некоторой точки твердого тела, ни первая производная 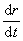 , ни вторая производная
, ни вторая производная 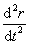 не могут служить характеристикой движения всего твердого тела.
не могут служить характеристикой движения всего твердого тела.
За это же время dt радиус-вектор 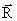 , проведенный из точки 0' в точку М, повернется на угол dφ. На такой же угол повернется радиус-вектор любой другой точки (т.к. тело абсолютно твердое, в противном случае расстояние между точками должно измениться).
, проведенный из точки 0' в точку М, повернется на угол dφ. На такой же угол повернется радиус-вектор любой другой точки (т.к. тело абсолютно твердое, в противном случае расстояние между точками должно измениться).
Угол поворота dφ характеризует перемещение всего тела за время dt.
Удобно ввести 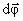 – вектор элементарного поворота тела, численно равный dφ и направленный вдоль оси вращения ОО' так, чтобы, глядя вдоль вектора, мы видели вращение по часовой стрелке (направление вектора
– вектор элементарного поворота тела, численно равный dφ и направленный вдоль оси вращения ОО' так, чтобы, глядя вдоль вектора, мы видели вращение по часовой стрелке (направление вектора 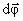 и направление вращения связаны «правилом буравчика»).
и направление вращения связаны «правилом буравчика»).
Элементарные повороты удовлетворяют обычному правилу сложения векторов:
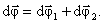
Угловой скоростью называется вектор 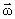 , численно равный первой производной от угла поворота по времени и направленный вдоль оси вращения в направлении
, численно равный первой производной от угла поворота по времени и направленный вдоль оси вращения в направлении 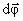 (
( 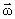 и
и 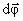 всегда направлены в одну сторону).
всегда направлены в одну сторону).
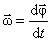 . .
| (2.4.1) |
Если ω – const, то имеет место равномерное вращение тела вокруг неподвижной оси.
Пусть v – линейная скорость точки М. За промежуток времени dt точка М проходит путь dr = vdt. В то же время dr = Rdφ (dφ - центральный угол). Тогда, можно получить связь линейной скорости и угловой:
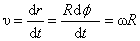 . .
| (2.4.2) |
В векторной форме 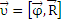 .
.
Вектор 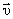 ортогонален к векторам
ортогонален к векторам 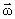 и
и 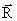 и направлен в ту же сторону, что и векторное произведение
и направлен в ту же сторону, что и векторное произведение 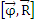 .
.
Наряду с угловой скоростью вращения используют понятия периода и частоты вращения.
Период Т – промежуток времени, в течение которого тело совершает полный оборот (т.е. поворот на угол φ = 2π).
Частота ν – число оборотов тела за 1 секунду.
При вращении с угловой скоростью ω имеем:
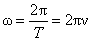 ,
, 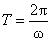 ,
, 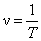 .
.
Введем вектор углового ускорения 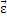 для характеристики неравномерного вращения тела:
для характеристики неравномерного вращения тела:
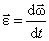 . .
| (2.4.3) |
Вектор 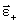 направлен в ту же сторону, что и
направлен в ту же сторону, что и 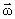 при ускоренном вращении
при ускоренном вращении 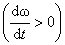 , а
, а 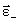 направлен в противоположную сторону при замедленном вращении
направлен в противоположную сторону при замедленном вращении 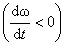 (рис. 2.13).
(рис. 2.13).
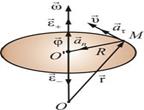
Рис. 2.13
Как и любая точка твердого тела, точка М имеет нормальную и тангенциальную составляющие ускорения. Выразим нормальное и тангенциальное ускорение точки М через угловую скорость и угловое ускорение:
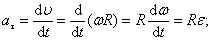
| |||
| aτ = Rε; | (2.4.4) | ||
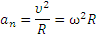
| |||
Дата: 2019-05-29, просмотров: 388.