Третье начало термодинамики связано с теоремой Нернста (тепловой теоремой). Третье начало представляет собой физический принцип, который является определяющим для поведения энтропии, когда температура приближается к абсолютному нулю. Третье начало термодинамики представляет собой один из постулатов, принятых на основании обобщения большого объема экспериментальных данных термодинамики гальванических элементов. Теорема была сформулирована В. Нерстом в 1906 г. Ее современная версия была предложена М. Планком. Следствием третьего начала считается невозможность охлаждения тела до абсолютного нуля, которую выражает принцип недостижимости. Иначе допускалась бы возможность существования вечного двигателя 2-го рода. Формулировка Нернста для третьего начала термодинамики Согласно утверждениям теоремы Нернста, всякий термодинамический процесс, который может протекать при фиксированной температуре (близкой к нулевой) не должен сопровождаться при этом изменением энтропии. Другими словами, изотерма будет совпадать с предельной адиабатой.

Существует несколько формулировок для теоремы Нернста, эквивалентных между собой: При абсолютном нулевом значении температуры энтропия любой системы представляет собой универсальную постоянную. Она не зависит от каких-либо переменных параметров (например, объема или давления). Энтропия (при приближении к абсолютному нулевому значению) будет стремиться к определенному конечному пределу, который не зависит от конечного состояния системы. Приращение энтропии (при приближении к абсолютному нулю) не будет зависеть от конкретных значений для термодинамических параметров состояния системы. Данный показатель стремится к определенному конечному пределу. При абсолютном нулевом значении все процессы, при которых система из одного равновесного состояния переходит в другое, осуществляются без изменения энтропии.

Математически можно это записать так:

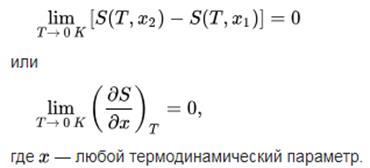
Рисунок 1. Формулировка Нернста.
Третье начало термодинамики имеет непосредственное отношение только к равновесным состояниям. Справедливость теоремы Нернста можно доказать только опытной проверкой ее следствий.
Третье начало термодинамики можно использовать для точного определения энтропии. При этом энтропия равновесной системы (при абсолютном нуле температур) считается равной нулю.

Третье начало термодинамики позволяет найти абсолютное значение энтропии, что невозможно осуществить в пределах классической термодинамики (на основе первого и второго начал). Энтропия в классической термодинамике может определяться только с точностью до произвольной аддитивной постоянной. Это, в свою очередь, не мешает проведению термодинамических исследований, поскольку становится возможным реальное измерение разности в различных состояниях:

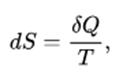
Рисунок 2. Формула.
Таким образом, понять суть теоремы Нернста можно на основании следующего примера. С уменьшением температуры газа начнется процесс его конденсации и убывания энтропии системы. Это объясняется более упорядоченным размещением молекул. С последующим уменьшением температуры начнется кристаллизация жидкости. Этот процесс будет сопровождаться еще большей упорядоченностью молекулярного расположения и еще более значительным убыванием энтропии.

При абсолютном нуле температуры будет прекращено любое тепловое движение, исчезнет неупорядоченность, уменьшится число возможных микросостояний до одного, а энтропия приблизится к нулю.

Формулировка Планка для третьего начала термодинамики

В 1911 году М. Планк сформулировал третье начало термодинамики, при котором энтропия всех тел обращается в ноль, когда температура стремиться к нулевому значению.

Это позволяет определять абсолютные значения энтропии и остальных термодинамических потенциалов. Формулировка Планка является соответствием определению энтропии в статистической физике с помощью термодинамической вероятности состояния системы:

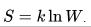
Рисунок 3. Формулировка Планка.
Система (при абсолютном нуле температуры) пребывает в базовом квантово-механическом состоянии. Если оно не вырождено, энтропия равна нулю и состояние реализуется единственно возможным микрораспределением.

 На самом деле, стремление энтропии к нулю при всех измерениях начинает проявляться гораздо раньше, чем могут стать существенными воздействие квантового вырождения и дискретность квант-уровней макроскопической системы.

Согласно третьему началу термодинамики, достичь абсолютного нуля температуры нельзя ни в каком конечном процессе, имеющим отношение к изменению энтропии. К нему возможно приблизиться только асимптотически. По этой причине третье начало термодинамики иногда формулируются в виде принципа недостижимости абсолютного нуля температур.
Нарушения третьего начала термодинамики Из третьего начала термодинамики вытекают определенные термодинамические следствия: при

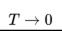
должны будут стремиться к нулевому значению теплоемкости (при постоянном давлении и объеме), а также коэффициенты теплового расширения и некоторые из аналогичных величин.

Некоторое время справедливость 3-го начала термодинамики подвергалась сомнению, однако позднее ученым удалось выяснить, что все изначально кажущиеся противоречия (ненулевое значение энтропии для ряда веществ) при

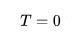
взаимосвязаны с метастабильными состояниями вещества, которые не считаются термодинамически равновесными).

Третье начало термодинамики зачастую нарушается в модельных системах. Так, при

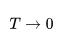
энтропия у классического идеального газа будет стремиться к минус бесконечности. Это означает, что уравнение Менделеева-Клапейрона при низких температурах некорректно описывает поведение реальных газов.

Третье начало термодинамики, таким образом, демонстрирует недостаточность статистики и классической механики и служит макроскопическим проявлением квантовых качеств в отношении реальных систем.

В модельных системах (в квантовой механике) третье начало может быть нарушено. Это могут быть случаи применения распределения Гиббса.

В то же время несоблюдение 3-го начала в модели не исключает, что в каком-то отдельном диапазоне изменения физических величин данная модель может быть вполне адекватной.