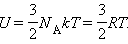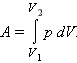Термодинамика – это наука о тепловых явлениях. В противоположность молекулярно-кинетической теории, которая делает выводы на основе представлений о молекулярном строении вещества, термодинамика исходит из наиболее общих закономерностей тепловых процессов и свойств макроскопических систем. Выводы термодинамики опираются на совокупность опытных фактов и не зависят от наших знаний о внутреннем устройстве вещества, хотя в целом ряде случаев термодинамика использует молекулярно-кинетические модели для иллюстрации своих выводов.
Термодинамика рассматривает изолированные системы тел, находящиеся в состоянии термодинамического равновесия. Это означает, что в таких системах прекратились все наблюдаемые макроскопические процессы. Важным свойством термодинамически равновесной системы является выравнивание температуры всех ее частей.
Если термодинамическая система была подвержена внешнему воздействию, то в конечном итоге она перейдет в другое равновесное состояние. Такой переход называется термодинамическим процессом. Если процесс протекает достаточно медленно (в пределе бесконечно медленно), то система в каждый момент времени оказывается близкой к равновесному состоянию. Процессы, состоящие из последовательности равновесных состояний, называются квазистатическими.
Одним из важнейших понятий термодинамики является внутренняя энергия тела. Все макроскопические тела обладают энергией, заключенной внутри самих тел. С точки зрения молекулярно-кинетической теории внутренняя энергия вещества складывается из кинетической энергии всех атомов и молекул и потенциальной энергии их взаимодействия друг с другом. В частности, внутренняя энергия идеального газа равна сумме кинетических энергий всех частиц газа, находящихся в непрерывном и беспорядочном тепловом движении. Отсюда вытекает закон Джоуля, подтверждаемый многочисленными экспериментами.
| Внутренняя энергия идеального газа зависит только от его температуры и не зависит от объема |
Молекулярно-кинетическая теория приводит к следующему выражению для внутренней энергии одного моля идеального одноатомного газа (гелий, неон и др.), молекулы которого совершают только поступательное движение:
|
Поскольку потенциальная энергия взаимодействия молекул зависит от расстояния между ними, в общем случае внутренняя энергия U тела зависит наряду с температурой Tтакже и от объема V:
| U = U (T, V). |
Таким образом, внутренняя энергия U тела однозначно определяется макроскопическими параметрами, характеризующими состояние тела. Она не зависит от того, каким путем было реализовано данное состояние. Принято говорить, что внутренняя энергия является функцией состояния.
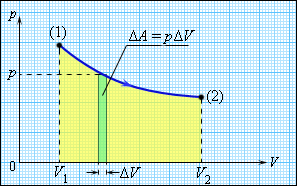
Внутренняя энергия тела может изменяться, если действующие на него внешние силы совершают работу (положительную или отрицательную). Например, если газ подвергается сжатию в цилиндре под поршнем, то внешние силы совершают над газом некоторую положительную работу A'. В то же время силы давления, действующие со стороны газа на поршень, совершают работу A = –A'. Если объем газа изменился на малую величину ΔV, то газ совершает работу pSΔx = pΔV, где p – давление газа, S – площадь поршня, Δx – его перемещение (рис. 3.8.1). При расширении работа, совершаемая газом, положительна, при сжатии – отрицательна. В общем случае при переходе из некоторого начального состояния (1) в конечное состояние (2) работа газа выражается формулой:
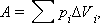
|
или в пределе при ΔVi → 0:
|
|
| Рисунок 3.8.1. Работа газа при расширении |
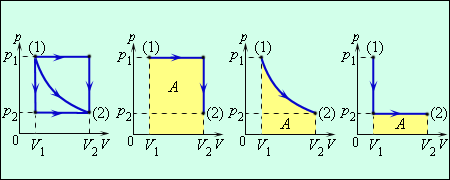
Работа численно равна площади под графиком процесса на диаграмме (p, V). Величина работы зависит от того, каким путем совершался переход из начального состояния в конечное. На рис. 3.8.2 изображены три различных процесса, переводящих газ из состояния (1) в состояние (2). Во всех трех случаях газ совершает различную работу.
|
| Рисунок 3.8.2. Три различных пути перехода из состояния (1) в состояние (2). Во всех трех случаях газ совершает разную работу, равную площади под графиком процесса |
Процессы, изображенные на рис. 3.8.2, можно провести и в обратном направлении; тогда работа A просто изменит знак на противоположный. Процессы такого рода, которые можно проводить в обоих направлениях, называются обратимыми (см. §3.12).
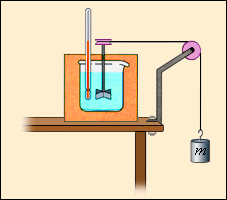
В отличие от газа, жидкости и твердые тела мало изменяют свой объем, так что во многих случаях работой, совершаемой при расширении или сжатии, можно пренебречь. Однако, внутренняя энергия жидких и твердых тел также может изменяться в результате совершения работы. При механической обработке деталей (например, при сверлении) они нагреваются. Это означает, что изменяется их внутренняя энергия. Другим примером может служить опыт Джоуля (1843 г.) по определению механического эквивалента теплоты (рис. 3.8.3). При вращении вертушки, погруженной в жидкость, внешние силы совершают положительную работу (A' > 0); при этом жидкость из-за наличия сил внутреннего трения нагревается, т. е. увеличивается ее внутренняя энергия. В этих двух примерах процессы не могут быть проведены в противоположном направлении. Такие процессы называются необратимыми.
|
| Рисунок 3.8.3. Упрощенная схема опыта Джоуля по определению механического эквивалента теплоты |
Внутренняя энергия тела может изменяться не только в результате совершаемой работы, но и вследствие теплообмена. При тепловом контакте тел внутренняя энергия одного из них может увеличиваться, а другого – уменьшаться. В этом случае говорят о тепловом потоке от одного тела к другому. Количеством теплоты Q, полученным телом, называют изменение внутренней энергии тела в результате теплообмена.

|
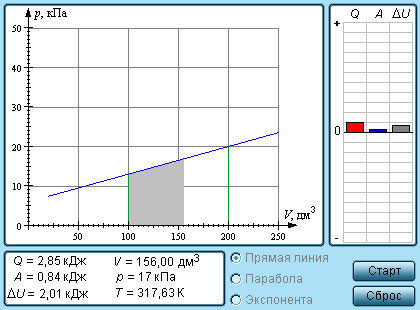
| Модель. Работа газа |
Передача энергии от одного тела другому в форме тепла может происходить только при наличии разности температур между ними.
Тепловой поток всегда направлен от горячего тела к холодному.
Количество теплоты Q является энергетической величиной. В СИ количество теплоты измеряется в единицах механической работы – джоулях (Дж).
Запишем первое начало термодинамики для различных изопроцессов и адиабатического.
Начнём рассмотрение с изобарного процесса.
1) P=const; m=const.
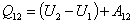
| (53.1) |
- интегральная запись первого начала термодинамики для изобарного процесса.
В изобарном процессе всё полученное системой количество теплоты идёт на приращение внутренней энергии и совершение работы против внешних сил.
Но для него также выполняется закон Гей-Люссака:
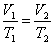
| (53.2) |
а работа в изобарном процессе равна:
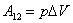
| (53.3) |
Приращение объёма найдем из закона Гей – Люссака:
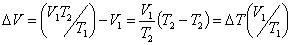
| (53.4) |
Теперь, подставим приращение объёма при постоянном давлении и ав формулу для расчёта работы (53.3), получим:
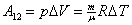
| (53.5) |
Из определения приращения внутренней энергии получаем:
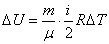
| (53.6) |
Теперь сравним соотношения для расчёта работы (53.5) и приращения внутренней энергии (53.6) в изобарном процессе и получим формулу связи между ними:
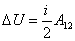
| (53.7) |
Или
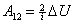
| (53.7) |
Теперь соотношение (53.1) можем представить ещё в двух формах записи:
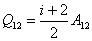
| (53.8) |
или
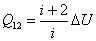
| (53.9) |
А если выразить количество теплоты, полученное системой в изобарном процессе через молярную теплоёмкость при постоянном давлении, то получим:
| Q12=(m/μ)Ср·ΔT | (53.10) |
Иногда приходится разбивать реальный процесс на элементарные процессы и тогда выражение для первого начала в дифференциальной форме будет иметь вид:
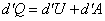
| (53.11) |
Соотношение (53.11) удобно использовать при решениях задач по разделу термодинамика.
2) Рассмотрим изохорный процесс.
V=const; m=const; A12=0; dA=0.
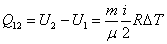
| (53.12) |
– интегральная форма записи первого начала термодинамики для изохорного процесса.
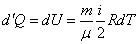
| (53.13) |
– дифференциальная форма записи первого начала термодинамики для изохорного процесса.
Таким образом, в изохорном процессе всё полученное системой количество теплоты идёт на приращение внутренней энергии.
3) Рассмотрим изотермический процесс:
Т=const; m=const; ΔU=0, A12≠0
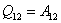
| (53.14) |
- интегральная запись первого начала термодинамики для изотермического процесса.
В изотермическом процессе всё полученное системой количество теплоты идёт на совершение работы против внешних сил.
4) Адиабатный процесс.
По определению - адиабатный процесс происходит без теплообмена с окружающей средой: Q12=0, тогда интегральная форма записи первого начала термодинамики для адиабатного процесса имеет вид:
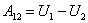
| (53.15) |
Из соотношения (53.15) следует:
в адиабатном процессе работа совершается только за счёт убыли внутренней энергии.
Представим соотношение (53.15) в другом виде, выразив в выражении для внутренней энергии число степеней свободы через показатель адиабаты:
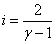
| (53.16) |
Теперь
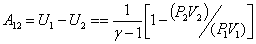
| (53.17) |
А в дифференциальной форме записи первое начало термодинамики для адиабатного процесса имеет вид:
dQ=0, тогда
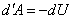
|
Адиабатный процесс — это процесс, происходящий без теплообмена системы с окружающей средой, т.е. Q = 0. Первый закон термодинамики имеет вид:
ΔU+A=0⇒A=−ΔU. ΔU+A=0⇒A=−ΔU.
Это значит, что при адиабатном процессе система может выполнять работу над внешними телами только за счет убыли своей внутренней энергии. Если А > 0, то ΔU = -A < 0, т.е. U2 < U1, а так как U=i2mMRT U=i2mMRT, то T2 < T1.
Как известно, газ совершает положительную работу, если ΔV > 0.
Таким образом, при адиабатном расширении газ совершает работу и сам охлаждается. Наоборот, при адиабатном сжатии А < 0 над газом совершается работа и газ нагревается.
При адиабатном процессе давление и объем связаны между собой уравнением
pVγ=const. pVγ=const.
где γ > 1 — показатель адиабаты (или коэффициент Пуассона). Это уравнение называется уравнением адиабаты или уравнением Пуассона.
Адиабатное изменение состояния газа можно выразить графически. График этого процесса называют адиабатой. При одних и тех же начальных условиях (p0, V0) при адиабатном расширении давление газа уменьшается быстрее, чем при изотермическом (рис. 1), так как падение давления вызвано не только увеличением объема (как при изотермическом расширении), но и понижением температуры. Поэтому адиабата идет ниже изотермы и газ при адиабатном расширении совершает меньшую работу, чем при изотермическом расширении.
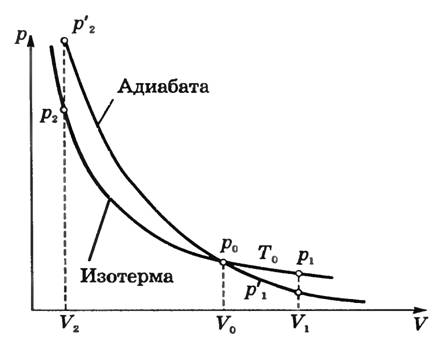
Рис. 1
При быстром сжатии (расширении) теплообмен произойти не успевает и процессы можно рассматривать как адиабатные (неравновесные). Поэтому любой газ при быстром сжатии нагревается (например, нагревание насоса при накачивании велосипедной шины). При сильном и быстром сжатии воздуха температура может повыситься настолько, что при наличии в воздухе паров бензина они воспламеняются. Это используется в дизельных двигателях для зажигания горючей смеси. Этим объясняется необходимость специального охлаждения мощных компрессоров.
Охлаждение воздуха при адиабатном расширении вызывает образование облаков.
Дата: 2019-05-29, просмотров: 475.