Изменение кинетической энергии материальной точки на некотором ее перемещении равняется алгебраической сумме робот всех действующих на точку сил на том же перемещении.
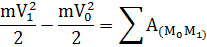
Теорема об изменении кинетической энергии механической системы
Изменение кинетической энергии механической системы на некотором перемещении равняется алгебраической сумме робот внутренних и внешних сил, действующих на материальные точки системы на том же перемещении.
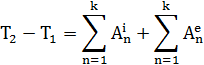
Теорема об изменении кинетической энергии твердого тела
Изменение кинетической энергии твердого тела (неизменной системы ) на некотором перемещении равняется сумме робот внешних сил, действующих на точки системы на том же перемещении.
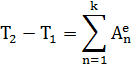
Примеры, рассмотренные ниже, дают результаты, которыми можно пользоваться при решении задач.
 1. Работа равнодействующей силы. Теорема: Работа равнодействующей силы на некотором перемещении равна алгебраической сумме работ составляющих сил на том же перемещении.
1. Работа равнодействующей силы. Теорема: Работа равнодействующей силы на некотором перемещении равна алгебраической сумме работ составляющих сил на том же перемещении.
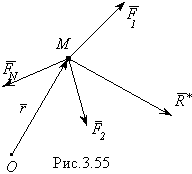
Допустим, что на точку действуют силы 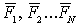 (рис.3.55)
(рис.3.55)
Равнодействующая этих сил 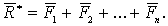
Если точка M получает элементарное перемещение 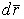 , то элементарная работа равнодействующей силы
, то элементарная работа равнодействующей силы 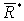 на этом перемещении
на этом перемещении
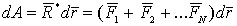 . Для вычисления работы равнодействующей силы на участке
. Для вычисления работы равнодействующей силы на участке 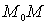 воспользуемся формулой (3.103)
воспользуемся формулой (3.103)
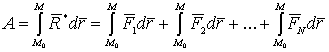 , или
, или
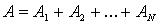 . (3.106)
. (3.106)
 2. Работа силы тяжести. Найдем сначала работу силы тяжести для точки. Пусть точка, на которую действует сила тяжести
2. Работа силы тяжести. Найдем сначала работу силы тяжести для точки. Пусть точка, на которую действует сила тяжести 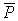 перемещается из положения
перемещается из положения 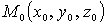 в положение
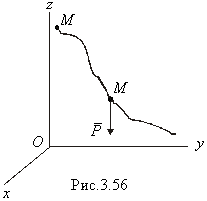
в положение 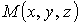 . Выберем оси координат так, чтобы ось z была направлена вертикально вверх (рис.3.56).
. Выберем оси координат так, чтобы ось z была направлена вертикально вверх (рис.3.56).
В этом случае 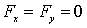 ,
, 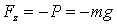 .
. 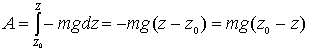 .
.
Обозначим 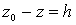 , где h - величина вертикального перемещения точки. Если точка
, где h - величина вертикального перемещения точки. Если точка 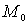 выше
выше 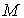 , то
, то 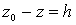 , если же точка
, если же точка 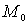 ниже
ниже 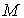 , то
, то 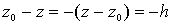 . Поэтому
. Поэтому
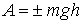 , (3.107)
, (3.107)
т.е. работа силы тяжести равна взятому со знаком плюс или минус произведению силы тяжести на вертикальное перемещение точки ее приложения. Работа положительна, если точка опускается, и отрицательна, если точка поднимается.
Для механической системы работа силы тяжести K-ой точки будет 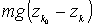 . Тогда сумма работ всех сил тяжести, действующих на систему:
. Тогда сумма работ всех сил тяжести, действующих на систему:
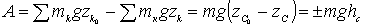 , (3.108)
, (3.108)
где mg - сила тяжести системы, 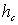 - вертикальное перемещение центра масс системы.
- вертикальное перемещение центра масс системы.
6. Консервативные и неконсервативные силы. Потенциальная энергия.
Силы, действующие на тело, могут быть консервативными и неконсервативными. Сила называется консервативной или потенциальной, если работа, совершаемая этой силой при перемещении материальной точки из одного положения в другое, не зависит от вида траектории (формы пути) и определяется только начальным и конечным положениями тела (рис.3.1): А1В2 = А1С2 = А12.
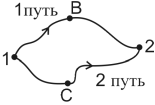
Рис.3.1
В случае, если тело движется в обратном направлении А12= –А21, т.е. изменение направления движения по траектории на противоположное вызывает изменение знака работы. Следовательно, при движении материальной точки по замкнутой траектории работа консервативной силы равна нулю (например, поднятие и опускание груза):
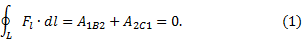
Консервативными силами являются силы гравитационного взаимодействия, силы упругости, электростатические силы. Силы, не удовлетворяющие условию (1), называются неконсервативными. К неконсервативным силам относят силы трения и сопротивления. Поле, в котором действуют консервативные силы, называется потенциальным.
Конечно, помимо консервативных сил есть неконсервативные. Это все остальные силы, чья работа вычисляется по пути.
Неконсервативные силы:
Сила трения
Сила трения возникает при движении одного тела по поверхности другого и равна:
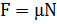
μ - коэффициент трения,
N - сила реакции опоры.
Коэффициент трения зависит от материала тел, состояния их поверхности и т. д., но он не зависит от площади трущихся тел.
Сила сопротивления воздуха
Сила сопротивления воздуха возникает, когда тело какой-то формы движется со скоростью V в воздухе. Для некоторого диапазона скоростей эта сила пропорциональна квадрату скорости:
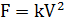
k - коэффициент пропорциональности, зависящий от формы движущегося тела и его прочих характеристик.
Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями (так называемые консервативные силы). Работа таких сил на замкнутой траектории равна нулю. Таким свойством обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.
Потенциальная энергия тела в поле силы тяжести Земли рассчитывается по формуле:
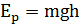
Физический смысл потенциальной энергии тела: потенциальная энергия равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень (h – расстояние от центра тяжести тела до нулевого уровня). Если тело обладает потенциальной энергией, значит оно способно совершить работу при падении этого тела с высоты h до нулевого уровня. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:
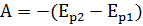
Дата: 2019-05-29, просмотров: 368.