В зависимости от характера воздействия, оказываемого на колеблющуюся систему, различают свободные ( или собственные) колебания, вынужденные колебания, автоколебания и параметрические колебания.
Вынужденными называются такие колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодически изменяющейся силы. Примером могут служить колебания моста, возникающие при прохождении по нему людей, шагающих в ногу.
Пусть вынуждающая сила изменяется со временем по гармоническому закону
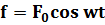 (1)
(1)
При составлении уравнения движения нужно учесть, кроме вынуждающей силы, также квазиупругую силу и силу сопротивления среды. Тогда уравнение запишется в виде:
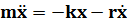 +
+ 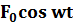
Разделив это уравнение на m и перенеся члены с х на 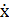 в левую часть, получим неоднородное линейное дифференциальное уравнение второго порядка:
в левую часть, получим неоднородное линейное дифференциальное уравнение второго порядка:
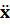 + 2
+ 2 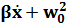 x =
x =  (2)
(2)
где  ,
, 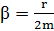 - коэффициент затухания,
- коэффициент затухания,
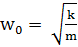 - собственная частота колебаний системы.
- собственная частота колебаний системы.
Как известно из теории дифференциальных уравнений, общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения.
Общем решением однородного уравнения 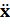 + 2
+ 2 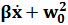 x =
x = 
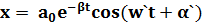 (3)
(3)
Где 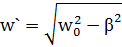 , а
, а 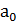 и
и 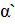 - произвольные постоянные.
- произвольные постоянные.
Остается найти частное (не содержащее произвольных постоянных). Предположим, что это решение имеет вид
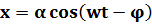 (4)
(4)
В данном случае удобно обозначить начальную фазу через  . С помощью векторной диаграммы можно определить значения а и
. С помощью векторной диаграммы можно определить значения а и  , при которых функция (4) удовлетворяет уравнению (2). Дифференцируя (4) по времени, первые 2 члена можно представить в виде:
, при которых функция (4) удовлетворяет уравнению (2). Дифференцируя (4) по времени, первые 2 члена можно представить в виде:
 = -2
= -2 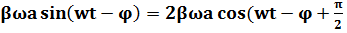 ) (5)
) (5)
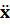 = -
= -  (6)
(6)
Как следует из (1), гармоническое колебание
 является суммой трех гармонических колебаний той же частоты: колебания (5),(6) и
является суммой трех гармонических колебаний той же частоты: колебания (5),(6) и 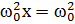 a cos (wt-
a cos (wt- 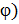
Рис.1
Если изобразить последнее колебание вектором длины 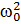 a, направленным вправо, то колебание изобразится вектором длины
a, направленным вправо, то колебание изобразится вектором длины 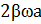 , повернутым относительно вектора
, повернутым относительно вектора 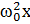 против часовой стрелки на угол
против часовой стрелки на угол  , а колебание (6) – вектором длины
, а колебание (6) – вектором длины 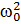 a, повернутым относительно вектора
a, повернутым относительно вектора 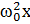 на угол
на угол 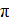 . Чтобы уравнение (2) было удовлетворено, векторная сумма перечисленных трех векторов должна совпадать с вектором, изображающим колебание
. Чтобы уравнение (2) было удовлетворено, векторная сумма перечисленных трех векторов должна совпадать с вектором, изображающим колебание  . Такое совпадение возможно лишь при значении амплитуды а, которое определяется условием рис 1. (а)
. Такое совпадение возможно лишь при значении амплитуды а, которое определяется условием рис 1. (а)
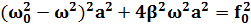
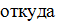
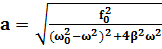 (7)
(7)
Рис1. (а) отвечает случаю 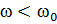 . Из рис.1.(б) соответствующего случаю
. Из рис.1.(б) соответствующего случаю  , получается такое же значение а.
, получается такое же значение а.
Рис1. Позволяет получить также и значение  , которое представляет собой величину отставания по фазе вынужденного колебания (4) от обусловившей его вынуждающей силы (1). Из рисунка следует, что
, которое представляет собой величину отставания по фазе вынужденного колебания (4) от обусловившей его вынуждающей силы (1). Из рисунка следует, что
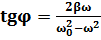 (8)
(8)
Подставив в (4) значение а и  , определяемые формулами (5) и (6), получим частное решение неоднородного уравнения (4) :
, определяемые формулами (5) и (6), получим частное решение неоднородного уравнения (4) :
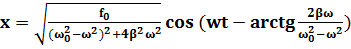 (9)
(9)
Функция (9) в сумме с (3) дает общее решение уравнения (2), описывающее поведение системы при вынужденных колебаниях. Функция (9) описывает установившиеся вынужденные колебания. Они представляют собой гармонические колебания с частотой, равной частоте вынуждающей силы. Амплитуда (7) вынужденных колебаний пропорциональна амплитуде вынуждающей силы. Для данной колебательной системы (определенных 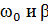 ) ампилтуда зависит от частоты вынуждающей силы. Вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания
) ампилтуда зависит от частоты вынуждающей силы. Вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания  также зависит от частоты вынуждающей силы.
также зависит от частоты вынуждающей силы.
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Колебательная система оказывается особенно отзывчивой на действие вынуждающей силы при этой частоте. Это явление называется резонансом, а соответствующая частота – резонансной частотой.
С явлением резонанса приходится считаться при конструировании машин и различного рода сооружений. Собственная частота колебаний этих устройств ни в коем случае не должна быть близка к частоте возможных внешних воздействий. Так, например, собственная частота вибраций корпуса корабля или крыльев самолета должна сильно отличаться от частоты колебаний, которые могут быть возбуждены вращением гребного винта или пропеллера. В противном случае возникают вибрации, которые могут вызвать катастрофу.
Основные положения молекулярно-кинетической теории строения вещества. Основное уравнение молекулярно-кинетической теории газов. Давление газов. Уравнение Менделеева – Клапейрона. Температура. Способы построения температурных шкал.
Молекулярно-кинетической теорией (МКТ) называют учение о строении и свойствах вещества на основе представления о существовании атомов и молекул как наименьших частиц химических веществ.
В основе молекулярно-кинетической теории лежат три основных положения:
1. Все вещества – жидкие, твердые и газообразные – образованы из мельчайших частиц – молекул, которые сами состоят из атомов («элементарных молекул»). Молекулы химического вещества могут быть простыми и сложными, т.е. состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы.
2. Атомы и молекулы находятся в непрерывном хаотическом движении. (доказательством является броуновское движение)
3. Частицы взаимодействуют друг с другом силами, имеющими электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало.
Дата: 2019-05-29, просмотров: 367.