Симплексный метод решения задач линейного программирования является универсальным, в основе которого является поэтапное улучшение решения. То есть переход от найденного решения к лучшему до тех пор, пока не будет найдено оптимальное решение.
Будем применять симплексный метод для решения задач, целью которых является максимум, и все ограничения имеют смысл ≤ за исключением ограничений неотрицательности переменных. То есть экономико-математическая модель задачи должна быть вида:
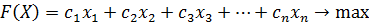
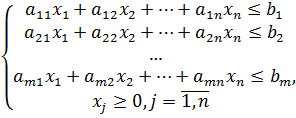
Алгоритм симплексного метода
I. Построение опорного плана.
1) От системы неравенств переходим к системе равенств путем введения дополнительных неотрицательных переменных (базисных):
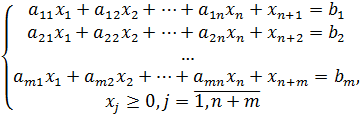
2) Все данные экономико-математической модели задачи переносим в симплекс-таблицу:
Таблица 1. Структура симлекс-таблицы
| базис |
| 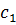
| 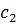
| … | 0 | … | 0 |
|

| 
| … | 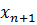
| … | 
| |||
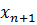
| 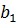
| 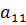
| 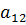
| … | 1 | … | 0 | |
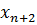
| 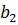
| 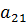
| 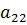
| … | 0 | … | 0 | |
| … | … | … | … | … | … | … | … | |

| 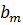
| 
| 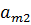
| … | 0 | … | 1 | |
| m+1 | 0 | 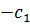
| 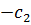
| … | 0 | … | 0 |
Последняя строка m +1 называется индексной и заполняется коэффициентами функции цели, взятыми с противоположными знаками.
II. Проверка плана на оптимальность.
Критерием оптимальности решения задачи является отсутствие отрицательных значений в индексной строке. Если есть хотя бы одно отрицательное значение в индексной строке, то план является неоптимальным и его нужно улучшать.
III. Улучшение плана.
Переход от одного плана к другому осуществляется по методу Жордано-Гаусса (методом «прямоугольника»). Для этого выполним последовательно несколько шагов.
1) Найдем разрешающий столбец. Из всех отрицательных значений индексной строки выбираем наибольшее значение по абсолютной величине, что и определяет разрешающий столбец.
2) Найдем разрешающую строку. Для этого элементы столбца
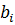 делим на положительные элементы разрешающего столбца и записываем в последний столбец. Из полученных значений выбираем наименьшее, что и определяет разрешающую строку.
делим на положительные элементы разрешающего столбца и записываем в последний столбец. Из полученных значений выбираем наименьшее, что и определяет разрешающую строку.
Разрешающая строка определяет переменную, которая из базиса на следующем этапе выйдет, а разрешающий столбец определяет переменную, которая на следующем этапе войдет в базис.
3) На пересечении разрешающего столбца и разрешающей строки находится разрешающий элемент, который для удобства нужно выделить кружком (таблица 2).
Таблица 2. Разрешающий элемент
| базис |
| 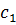
| 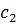
| … | 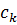
| … | 0 | … | 0 |
|

| 
| … | 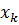
| … | 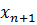
| … | 
| |||
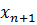
| 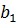
| 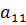
| 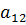
| … | 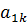
| … | 1 | … | 0 | 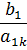
|
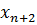
| 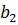
| 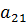
| 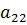
| … | 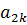
| … | 0 | … | 0 | 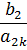
|
| … | … | … | … | … | … | … | … | … | … | |
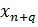
| 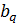
| 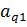
| 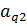
| … |  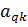
| … | 0 | … | 0 | 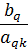
|
| … | … | … | … | … | … | … | … | … | … | |

| 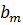
| 
| 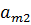
| … | 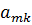
| … | 0 | … | 1 | 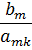
|
| m+1 | 0 | 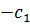
| 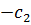
| … | 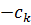
| … | 0 | … | 0 |
4) Новую таблицу начинаем заполнять с базисного столбца, заменяя переменную, которая из базиса вышла.
5) Заполняем ту строку, которая в предыдущей таблице была разрешающей и записываем в нее результаты деления элементов разрешающей строки на разрешающий элемент.
6) На пересечении переменных базиса со столбцами, в которых стоят они же, ставим 1, остальные значения в столбцах, в которых стоят базисные переменные, находятся нули, включая индексную строку.
7) Все остальные элементы новой симплекс-таблицы рассчитываются по формуле:
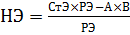 ,
,
где НЭ – новый элемент,
РЭ – разрешающий элемент,
А и В – элементы, образующие со старым и разрешающим элементами прямоугольник (рис. 1.6).
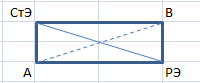
Рис. 1.6. Метод «прямоугольника»
Диагональ СтЭ РЭ – главная диагональ, диагональ АВ – второстепенная. Сначала перемножаются элементы, находящиеся на главной диагонали (на этой диагонали обязательно присутствует разрешающий элемент), затем элементы, находящиеся на второстепенной диагонали, находится их разность и полученное значение делится на разрешающий элемент.
IV. Проверка плана на оптимальность по пункту II.
Алгоритм с пункта II до пункта IV выполняется до тех пор, пока не выполнится критерий оптимальности.
При переходе к новому плану (симплекс-таблице) необходимо контролировать значение в столбце 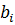 в индексной строке, которое не должно получиться отрицательным и меньшим, чем в предыдущей таблице.
в индексной строке, которое не должно получиться отрицательным и меньшим, чем в предыдущей таблице.
V. После получения оптимального плана записываем ответ. Максимальное значение функции находится в столбце 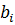 в индексной строке. Значения переменных, при которых получается максимальное значение функции, находятся в соответствующих строках столбца
в индексной строке. Значения переменных, при которых получается максимальное значение функции, находятся в соответствующих строках столбца 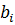 и базисного столбца.
и базисного столбца.
Пример 3. Решить симплексным методом задачу:
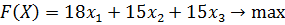
при ограничениях:
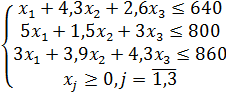
Решение.
I. Построение опорного плана.
1) От системы неравенств переходим к системе равенств путем введения дополнительных неотрицательных переменных (базисных):
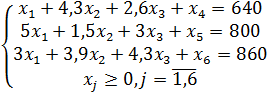
2) Занесем данные в симплекс-таблицу:
| базис |
| 18 | 15 | 15 | 0 | 0 | 0 |
|

| 
| 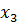
| 
| 
| 
| |||

| 640 | 1 | 4,3 | 2,6 | 1 | 0 | 0 | |

| 800 | 5 | 1,5 | 3 | 0 | 1 | 0 | |

| 860 | 3 | 3,9 | 4,3 | 0 | 0 | 1 | |
| m+1 | 0 | -18 | -15 | -15 | 0 | 0 | 0 |
II. В индексной строке есть отрицательные элементы, следовательно, план не оптимальный и его нужно улучшать.
III. Улучшение плана.
1) Найдем разрешающий столбец. В индексной строке наибольшим по абсолютной величине отрицательным значением является -18, следовательно, столбец  является разрешающим.
является разрешающим.
2) Найдем разрешающую строку. Для этого разделим элементы столбца 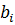 на положительные элементы разрешающего столбца и занесем результаты в последний столбец. Из полученных значений выбираем наименьшее 160, следовательно, разрешающей строкой будет строка, соответствующая базисному элементу
на положительные элементы разрешающего столбца и занесем результаты в последний столбец. Из полученных значений выбираем наименьшее 160, следовательно, разрешающей строкой будет строка, соответствующая базисному элементу  .
.
В новой таблице в базис вместо  перейдет переменная
перейдет переменная  .
.
3) Разрешающим элементом является элемент 5.
| базис |
| 18 | 15 | 15 | 0 | 0 | 0 |
|

| 
| 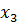
| 
| 
| 
| |||

| 640 | 1 | 4,3 | 2,6 | 1 | 0 | 0 | 640 |

| 800 |  5 5
| 1,5 | 3 | 0 | 1 | 0 | 160 |

| 860 | 3 | 3,9 | 4,3 | 0 | 0 | 1 | 286,7 |
| m+1 | 0 | -18 | -15 | -15 | 0 | 0 | 0 |
4), 5), 6)
| базис |
| 18 | 15 | 15 | 0 | 0 | 0 |
|

| 
| 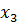
| 
| 
| 
| |||

| 0 | 1 | 0 | |||||

| 160 | 1 | 0,3 | 0,6 | 0 | 0,2 | 0 | |

| 0 | 0 | 1 | |||||
| m+1 | 0 | 0 | 0 |
7) Пересчитаем остальные элементы по формуле 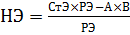 .
.
| базис |
| 18 | 15 | 15 | 0 | 0 | 0 |
|

| 
| 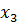
| 
| 
| 
| |||

| 480 | 0 | 4 | 2 | 1 | -0,2 | 0 | |

| 160 | 1 | 0,3 | 0,6 | 0 | 0,2 | 0 | |

| 380 | 0 | 3 | 2,5 | 0 | -0,6 | 1 | |
| m+1 | 2880 | 0 | -9,6 | -4,2 | 0 | 3,6 | 0 |
IV. План неоптимальный, так как есть отрицательные значения в индексной строке, следовательно его нужно улучшать.
III. Улучшение плана.
1) Найдем разрешающий столбец. В индексной строке наибольшим по абсолютной величине отрицательным значением является -9,6, следовательно, столбец  является разрешающим.
является разрешающим.
2) Найдем разрешающую строку. Для этого разделим элементы столбца 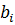 на положительные элементы разрешающего столбца и занесем результаты в последний столбец. Из полученных значений выбираем наименьшее 120, следовательно, разрешающей строкой будет строка, соответствующая базисному элементу
на положительные элементы разрешающего столбца и занесем результаты в последний столбец. Из полученных значений выбираем наименьшее 120, следовательно, разрешающей строкой будет строка, соответствующая базисному элементу 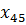 .
.
В новой таблице в базис вместо  перейдет переменная
перейдет переменная 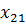 .
.
3) Разрешающим элементом является элемент 4.
| базис |
| 18 | 15 | 15 | 0 | 0 | 0 |
|

| 
| 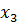
| 
| 
| 
| |||

| 480 | 0 |  4 4
| 2 | 1 | -0,2 | 0 | 120 |

| 160 | 1 | 0,3 | 0,6 | 0 | 0,2 | 0 | 533,3 |

| 380 | 0 | 3 | 2,5 | 0 | -0,6 | 1 | 126,7 |
| m+1 | 2880 | 0 | -9,6 | -4,2 | 0 | 3,6 | 0 |
4), 5), 6)
| базис |
| 18 | 15 | 15 | 0 | 0 | 0 |
|

| 
| 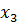
| 
| 
| 
| |||

| 120 | 0 | 1 | 0,5 | 0,25 | -0,05 | 0 | |

| 1 | 0 | 0 | |||||

| 0 | 0 | 1 | |||||
| m+1 | 0 | 0 | 0 |
7) Пересчитаем остальные элементы по формуле 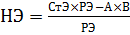
| базис |
| 18 | 15 | 15 | 0 | 0 | 0 |
|

| 
| 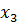
| 
| 
| 
| |||

| 120 | 0 | 1 | 0,5 | 0,25 | -0,05 | 0 | |

| 124 | 1 | 0 | 0,45 | -0,075 | 0,215 | 0 | |

| 20 | 0 | 0 | 1 | -0,75 | -0,45 | 1 | |
| m+1 | 4032 | 0 | 0 | 0,6 | 2,4 | 3,72 | 0 |
IV. План оптимальный, так как нет отрицательных значений в индексной строке.
Запишем ответ.
| базис |
| 18 | 15 | 15 | 0 | 0 | 0 |
| ||||

| 
| 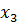
| 
| 
| 
| |||||||

| 120 | 0 | 1 | 0,5 | 0,25 | -0,05 | 0 | |||||

| 124 | 1 | 0 | 0,45 | -0,075 | 0,215 | 0 | |||||

| 20 | 0 | 0 | 1 | -0,75 | -0,45 | 1 | |||||
| m+1 | 4032 | 0 | 0 | 0,6 | 2,4 | 3,72 | 0 |

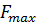
Ответ: максимальное значение целевой функции равно 4032 при  =124,
=124,  =120,
=120, 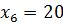 .
.
Практическое занятие 5
Выучите алгоритм симплексного метода.
Решите задачи симплексным методом.
1. На кондитерскую фабрику перед Новым годом поступили заказы на подарочные наборы конфет из трех магазинов. Возможные варианты наборов, их стоимость и товарные запасы на фабрике представлены в таблице:
| Наименование конфет | Вес конфет в наборе, кг | Запасы конфет, кг | ||
| А | В | С | ||
| Сникерс | 0,3 | 0,2 | 0,4 | 600 |
| Марс | 0,2 | 0,3 | 0,2 | 700 |
| Баунти | 0,2 | 0,1 | 0,1 | 500 |
| Цена, руб. | 72 | 62 | 76 | |
Определить оптимальное соотношение количества подарочных наборов, которые фабрика может предложить магазинам и обеспечить максимальный доход от продажи.
2. Фирма выпускает пластиковые пупсы, машинки и совки. В таблице приведены расход продуктов, суточное наличие на складе:
| Исходный продукт | Расход продуктов на 1 шт продукции | Запас на складе | ||
| пупс | машинка | совок | ||
| Пластмасса (кг) | 0,45 | 0,75 | 0,23 | 1000 |
| Затвердитель (г) | 16 | 14 | 12 | 1200 |
| Трудовые затраты (час) | 0,75 | 0,95 | 0,12 | 448 |
Суточный спрос на пупсов на 109 шт. выше, чем на машинки, а на совки на 14 шт. меньше, чем на машинки. Спрос на пупсов не более 130 штук. Отпускная цена пупса – 35 руб., машинки – 49 руб, совка – 5 руб.
3. Фирма выпускает бородинский, галицкий и рижский хлеб. В таблице приведены расход продуктов, суточное наличие запасов на складе:
| Исходный продукт | Расход продуктов на 1 шт продукции | Запас на складе | ||
| бородинский | галицкий | рижский | ||
| Мука( кг) | 0,45 | 0,39 | 0,55 | 1000 |
| Дрожжи (гр) | 16 | 14 | 12 | 1200 |
| молоко | 0,25 | 0,24 | 0,22 | 350 |
Суточный спрос на бородинский на 100 шт выше, чем на рижский, а на галицкий на 44 шт больше, чем на рижский. Спрос на бородинский не более 330 штук. Отпускная цена бородинского – 25 руб, галицкого – 19 руб, рижского– 27 руб. за буханку.
Домашнее задание:
Конкуренция приводит к необходимости торговым предприятиям заниматься еще и выпуском продукции собственного производства, например, пиццы. Нормы затрат на производство пиццы разных видов, объемы ресурсов и стоимость приведены в таблице:
| Продукты | Нормы затрат на изготовление 100 шт. пиццы, кг | Запасы продуктов, кг | ||
| ассорти | грибная | салями | ||
| Грибы | 6 | 7 | 2 | 20 |
| Колбаса | 5 | 2 | 8 | 18 |
| Тесто | 10 | 8 | 6 | 25 |
| Цена за 100 шт., тыс. руб. | 9 | 6 | 5 | |
Определите структуру выпуска пиццы разных видов для получения максимального дохода предприятия.
Дата: 2019-05-28, просмотров: 670.