В случае, когда целевая функция стремится к минимуму, а в условиях ограничений есть хотя бы одно неравенство смысла ≥, задача решается с помощью двойственного симплексного метода.
Алгоритм двойственного симплексного метода
I. Построение опорного плана.
1) В системе ограничений все неравенства смысла ≥ требуется привести к неравенствам смысла ≤. Для этого обе части неравенства смысла ≥ нужно умножить на (-1).
2) От системы неравенств переходим к системе равенств путем введения дополнительных неотрицательных переменных (базисных):
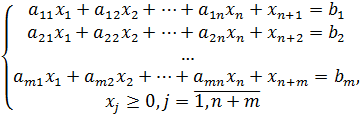
3) Все данные экономико-математической модели задачи переносим в симплекс-таблицу (табл. 3). Отличие таблицы для двойственного симплексного метода от таблицы для симплексного метода заключается в том, что в ней нет последнего столбца, но добавляется дополнительная строка 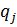 . Она потребуется для определения разрешающего столбца.
. Она потребуется для определения разрешающего столбца.
Таблица 3. Структура симлекс-таблицы для двойственного симплексного метода
| базис |
| 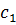
| 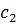
| … | 0 | … | 0 |

| 
| … | 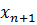
| … | 
| ||
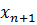
| 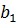
| 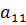
| 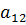
| … | 1 | … | 0 |
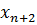
| 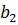
| 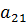
| 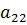
| … | 0 | … | 0 |
| … | … | … | … | … | … | … | … |

| 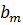
| 
| 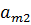
| … | 0 | … | 1 |
| m+1 | 0 | 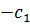
| 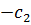
| … | 0 | … | 0 |
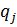
|
II. Проверка плана на оптимальность.
Критерием оптимальности решения задачи является отсутствие отрицательных значений в столбце 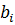 . Если есть хотя бы одно отрицательное значение в столбце
. Если есть хотя бы одно отрицательное значение в столбце 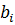 ., то план является неоптимальным и его нужно улучшать.
., то план является неоптимальным и его нужно улучшать.
III. Улучшение плана.
Переход от одного плана к другому осуществляется по методу Жордано-Гаусса (методом «прямоугольника»). Для этого выполним последовательно несколько шагов.
1) Найдем разрешающую строку. Для этого из всех отрицательных элементов столбца 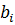 выбираем наибольшее по абсолютной величине отрицательное значение, что и определяет разрешающую строку.
выбираем наибольшее по абсолютной величине отрицательное значение, что и определяет разрешающую строку.
2) Найдем разрешающий столбец. Для этого заполним строку 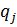 . Элементы строки
. Элементы строки 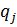 являются результатом деления отрицательных элементов индексной строки на отрицательные элементы разрешающей строки. Из полученных значений выбираем наименьшее, что и определяет разрешающий столбец.
являются результатом деления отрицательных элементов индексной строки на отрицательные элементы разрешающей строки. Из полученных значений выбираем наименьшее, что и определяет разрешающий столбец.
Разрешающая строка определяет переменную, которая из базиса на следующем этапе выйдет, а разрешающий столбец определяет переменную, которая на следующем этапе войдет в базис.
3) На пересечении разрешающего столбца и разрешающей строки находится разрешающий элемент, который для удобства нужно выделить кружком (таблица 2).
Таблица 2. Разрешающий элемент
| базис |
| 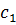
| 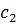
| … | 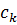
| … | 0 | … | 0 |

| 
| … | 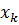
| … | 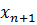
| … | 
| ||
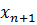
| 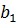
| 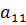
| 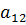
| … | 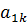
| … | 1 | … | 0 |
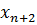
| 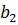
| 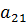
| 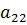
| … | 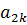
| … | 0 | … | 0 |
| … | … | … | … | … | … | … | … | … | … |
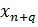
| 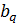
| 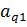
| 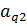
| … |  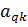
| … | 0 | … | 0 |
| … | … | … | … | … | … | … | … | … | … |

| 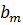
| 
| 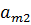
| … | 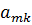
| … | 0 | … | 1 |
| m+1 | 0 | 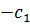
| 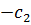
| … | 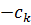
| … | 0 | … | 0 |
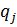
| 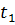
| 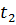
| … | 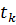
| … | 0 | … | 0 |
4) пункты 4), 5), 6), 7) выполняются так же, как и в симплексном методе.
IV. Проверка плана на оптимальность по пункту II.
Алгоритм с пункта II до пункта IV выполняется до тех пор, пока не выполнится критерий оптимальности.
V. После получения оптимального плана записываем ответ. Минимальное значение функции находится в столбце 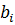 в индексной строке. Значения переменных, при которых получается максимальное значение функции, находятся в соответствующих строках столбца
в индексной строке. Значения переменных, при которых получается максимальное значение функции, находятся в соответствующих строках столбца 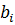 и базисного столбца.
и базисного столбца.
Пример 4. Решить двойственным симплексным методом задачу:
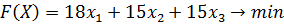
при ограничениях:
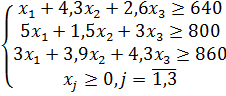
Решение.
I. Построение опорного плана.
1) В системе ограничений все неравенства смысла ≥ требуется привести к неравенствам смысла ≤. Для этого обе части неравенства смысла ≥ нужно умножить на (-1):
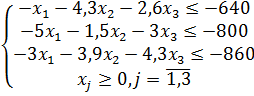
2) От системы неравенств переходим к системе равенств путем введения дополнительных неотрицательных переменных (базисных):
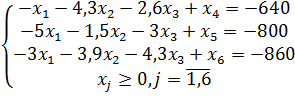
3) Все данные экономико-математической модели задачи переносим в симплекс-таблицу:
| базис |
| 18 | 15 | 15 | 0 | 0 | 0 |

| 
| 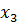
| 
| 
| 
| ||

| -640 | -1 | -4,3 | -2,6 | 1 | 0 | 0 |

| -800 | -5 | -1,5 | -3 | 0 | 1 | 0 |

| -860 | -3 | -3,9 | -4,3 | 0 | 0 | 1 |
| m+1 | 0 | -18 | -15 | -15 | 0 | 0 | 0 |
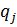
|
II. Проверка плана на оптимальность.
Полученный план не является оптимальным, так как есть отрицательные значения в столбце 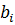 , следовательно, план нужно улучшать.
, следовательно, план нужно улучшать.
III. Улучшение плана.
1) Найдем разрешающую строку. Наибольшим по абсолютной величине отрицательным значением в столбце 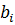 является число (-860), значит разрешающей строкой будет строка, соответствующая базисному элементу
является число (-860), значит разрешающей строкой будет строка, соответствующая базисному элементу  .
.
2) Найдем разрешающий столбец. Для этого заполним строку 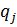 .
.
| базис |
| 18 | 15 | 15 | 0 | 0 | 0 |

| 
| 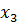
| 
| 
| 
| ||

| -640 | -1 | -4,3 | -2,6 | 1 | 0 | 0 |

| -800 | -5 | -1,5 |  -3 -3
| 0 | 1 | 0 |

| -860 | -3 | -3,9 | -4,3 | 0 | 0 | 1 |
| m+1 | 0 | -18 | -15 | -15 | 0 | 0 | 0 |
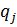
| 6 | 3,8 | 3,5 | - | - | - |
Наименьшее значение в строке 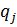 3,5, следовательно, разрешающим столбцом является столбец, соответствующий переменной
3,5, следовательно, разрешающим столбцом является столбец, соответствующий переменной 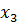 . Далее пересчитываем таблицу так же, как в симплексном методе по методу Жордано-Гаусса.
. Далее пересчитываем таблицу так же, как в симплексном методе по методу Жордано-Гаусса.
| базис |
| 18 | 15 | 15 | 0 | 0 | 0 |

| 
| 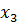
| 
| 
| 
| ||

| -120 | 0,8 | 2 | 0 | 1 | 0 | -0,6 |

| -200 | -2,9 | 1,2 | 0 | 0 | 1 | -0,7 |
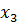
| 200 | 0,7 | 0,9 | 1 | 0 | 0 | -0,2 |
| m+1 | 3000 | -7,5 | -1,4 | 0 | 0 | 0 | -3,5 |
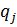
|
IV. План неоптимальный, так как в столбце 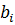 есть отрицательные значения, следовательно, план нужно улучшать.
есть отрицательные значения, следовательно, план нужно улучшать.
Далее последовательно выполняем пункты II – IV до тех пор, пока не будет выполняться критерий оптимальности.
| базис |
| 18 | 15 | 15 | 0 | 0 | 0 |

| 
| 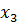
| 
| 
| 
| ||

| -120 | 0,8 | 2 | 0 | 1 | 0 | -0,6 |

| -200 |  -2,9 -2,9
| 1,2 | 0 | 0 | 1 | -0,7 |
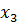
| 200 | 0,7 | 0,9 | 1 | 0 | 0 | -0,2 |
| m+1 | 3000 | -7,5 | -1,4 | 0 | 0 | 0 | -3,5 |
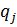
| 2,7 | 5 |
Результаты пересчета таблицы на данном этапе:
| базис |
| 18 | 15 | 15 | 0 | 0 | 0 |

| 
| 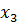
| 
| 
| 
| ||

| -175,1 | 0 | 2,3 | 0 | 1 | 0,3 |  -0,8 -0,8
|

| 68,9 | 1 | -0,4 | 0 | 0 | -0,3 | 0,2 |
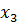
| 151,7 | 0 | 1,2 | 1 | 0 | 0,2 | -0,4 |
| m+1 | 3517,2 | 0 | -4,5 | 0 | 0 | -2,6 | -1,7 |
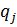
|
План неоптимальный. Пересчитаем симплекс-таблицу методом Жордано-Гаусса.
| базис |
| 18 | 15 | 15 | 0 | 0 | 0 |

| 
| 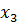
| 
| 
| 
| ||

| 218,9 | 0 | 0 | 1 | |||

| 25,1 | 1 | 0 | 0 | |||
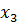
| 239,2 | 0 | 1 | 0 | |||
| m+1 | 3889,3 | 0 | 0 | 0 | |||
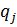
|
На последнем этапе, когда в столбце 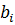 нет отрицательных значений, остальные значения таблицы можно не пересчитывать и записать ответ.
нет отрицательных значений, остальные значения таблицы можно не пересчитывать и записать ответ.
Ответ: минимальное значение целевой функции равно 3889,3 при 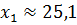 ,
, 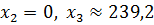 .
.
Практическое занятие 6
Выучите алгоритм двойственного симплексного метода.
Решите задачи двойственным методом.
1. 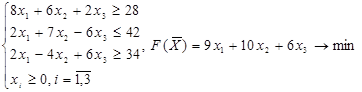
2. 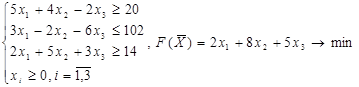
3. Постройте экономико-математическую модель определения структуры блюд на предприятии общественного питания, обеспечивающую максимальный доход на основе заданных нормативов затрат продуктов на первые и вторые блюда, представленных в таблице, и решите ее двойственным симплексным методом.
| Ресурсы | Плановый фонд ресурсов | Нормативные затраты на 100 блюд | ||||
| 1-е блюда | 2-е блюда мясные | 2-е блюда рыбные | 2-е блюда молочные | 2-е блюда прочие | ||
| Мясо, кг | 40000 | 4,0 | 8,0 | - | - | 3,8 |
| Рыба, кг | 25000 | 2,5 | - | 10 | - | - |
| Овощи, кг | 27000 | 3,2 | 2,0 | 3,0 | - | 4,6 |
| Мука, крупа, макаронные изделия, кг | 20000 | 2,1 | 2,6 | 2,3 | 3,2 | 2,8 |
| Молоко, л | 50000 | 6,5 | - | - | 21 | - |
| Доход, руб. | 1,3 | 2,0 | 1,5 | 0,3 | 1,7 | |
Домашнее задание:
Решить задачу двойственным методом:
1. 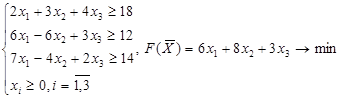
2. По предписанию врача пациенту необходимо перейти на диету для похудения и употреблять питательных веществ, содержащихся в продуктах, в количестве, указанном в таблице:
| Вещества | Содержание питательных веществ в 1 кг фруктов и ягод, г | Нормы потребления, г | ||
| Мясо | Рыба | Овощи | ||
| Белки | 250 | 180 | 10 | 140 |
| Жиры | 120 | 100 | 0 | 30 |
| Углеводы | 40 | 80 | 140 | 200 |
| Цена за 1 кг, руб. | 220,0 | 100,0 | 35,0 | |
Определить оптимальный план употребления продуктов с минимальными затратами.
Дата: 2019-05-28, просмотров: 503.