Основы математического моделирования социально-экономических процессов
Калининград
2018
УДК 330.101
ББК 65
Б21
Рецензенты:
канд. экон. наук, доцент Есенжулова Л. С., доцент кафедры экономики и менеджмента Западного филиала РАНХиГС
канд. физико-матем. наук, доцент Милованов В. Ф., доцент БФУ им. И. Канта
Б21 Балясникова Е. В., Скопич Д. Л.
Основы моделирования социально-экономических процессов /Е. В. Балясникова, Д. Л. Скопич. –Саратов: Амирит. 2018. – с.
Учебное пособие предназначено для студентов, обучающихся по направлениям 38.03.04 «Государственное и муниципальное управление», 38.03.02 «Менеджмент». Учебное пособие содержит основные материалы по дисциплине «Основы моделирования социально-экономических процессов». В нем представлены основные вопросы лекционного курса по дисциплине и для подготовки к практическим занятиям, задания для практического выполнения студентами, задания для выполнения на лабораторных занятиях с методическими рекомендациями по их выполнению.
Допущено (рекомендовано) Ученым советом Западного филиала РАНХиГС в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлениям 38.03.04 «Государственное и муниципальное управление», 38.03.02 «Менеджмент»
Учебное пособие рекомендовано к изданию Ученым советом филиала «__» ____________ 201_г., протокол №____.
.
© Балясникова Е. В., Скопич Д. Л.
©Западный филиал РАНХиГС, 2018
Оглавление
Раздел 1. Основные понятия математического моделирования социально-экономических процессов 4
Тема 1. Основные понятия и технология построения математических моделей социально-экономических процессов. 4
Практическое занятие 1. 17
Тема 2. Задачи управления социально-экономическими процессами как объект математического моделирования и прогнозирования. 18
Практическое занятие 2. 21
Раздел 2. Математические модели социально-экономических процессов принятия решений. Методы оптимизации. 22
Тема 3. Модели линейного программирования. 22
Практическое занятие 3. 26
Графический метод решения задач линейного программирования. 28
Практическое занятие 4. 33
Симплексный метод решения задач линейного программирования. 35
Практическое занятие 5. 42
Двойственный симплексный метод. 44
Практическое занятие 6. 49
Постановка и правила построения двойственной задачи. 50
Практическое занятие 7. 53
Транспортная задача. 54
Практическое занятие 8. 65
Решение задач линейного программирования инструментами MS Excel 66
Лабораторная работа по теме «Модели линейного программирования» 70
Тема 4. Специальные задачи линейного программирования. 97
Практическое занятие 9. 97
Тема 5. Динамическое программирование. 100
Практическое занятие 10. 107
Тема 6. Теоретико-игровые модели принятия решений. 108
Практическое занятие 11. 137
Тема 7. Прогнозирование с помощью парной и множественной регрессии. 140
Тема 8: Моделирование временных рядов. 152
Библиографический список. 160
Приложение А.. 162
Оформление титульного листа контрольной работы.. 162
Раздел 1. Основные понятия математического моделирования социально-экономических процессов
Тема 1. Основные понятия и технология построения математических моделей социально-экономических процессов
Рассмотрим ряд основных понятий, связанных с системным анализом и моделированием социально-экономических систем, чтобы с их помощью более полно раскрыть суть такого ключевого понятия, как экономико-математические методы. Термин "экономико-математические методы" понимается в свою очередь как обобщающее название комплекса экономических и математических научных дисциплин, объединенных для изучения социально-экономических систем и процессов.
Под социально-экономической системой понимают сложную вероятностную динамическую систему, охватывающую процессы производства, обмена, распределения и потребления материальных и других благ. Она относится к классу кибернетических систем, т. е. систем управляемых.
Центральным понятием кибернетики является понятие «система». Системой называется комплекс взаимосвязанных элементов вместе с отношениями между элементами и между их атрибутами. Исследуемое множество элементов можно рассматривать как систему, если выявлены четыре признака:
- целостность системы, т. е. принципиальная несводимость свойств системы к сумме свойств составляющих ее элементов;
- наличие цели и критерия исследования данного множества элементов,
- наличие более крупной, внешней по отношению к данной, системы, называемой «средой»;
- возможность выделения в данной системе взаимосвязанных частей (подсистем).
Основным методом исследования систем является метод моделирования, т. е. способ теоретического анализа и практического действия, направленный на разработку и использование моделей. При этом под моделью будем понимать образ реального объекта (процесса) в материальной или идеальной форме (т. е. описанный знаковыми средствами на каком-либо языке), отражающий существенные свойства моделируемого объекта (процесса) и замещающий его в ходе исследования и управления. Метод моделирования основывается на принципе аналогии, т. е. возможности изучения реального объекта не непосредственно, а через рассмотрение подобного ему и более доступного объекта, его модели. В дальнейшем мы будем говорить только об экономико-математическом моделировании, т. е. об описании знаковыми математическими средствами социально-экономических систем.
Моде́ль (фр. modèle, от лат. modulus — «мера, аналог, образец») — это система, исследование которой служит средством для получения информации о другой системе; представление некоторого реального процесса, устройства или концепции.
Модель есть абстрактное представление реальности в какой-либо форме (например, в математической, физической, символической, графической или дескриптивной), предназначенное для представления определенных аспектов этой реальности и позволяющее получить ответы на изучаемые вопросы
Моделирование это построение моделей, предназначенных для изучения и исследования объектов, процессов или явлений.
Поведение модели должно, так или иначе, отражать особенности поведения оригинала. Смысл моделирования заключается в том, что модель системы проще оригинала и ее исследование провести легче и дешевле. Изменение параметров модели позволит изучить их влияние на оригинал.
Основные цели моделирования в разных ситуациях:
1. Понимание и объяснение причин и факторов, влияющих на определенное поведение оригинала.
2. Прогноз поведения оригинала.
3. Разработка и проектирование технических систем или экономических планов.
4. Автоматизация управления техническими системами и устройствами.
5. Улучшение (оптимизация) характеристик той или иной искусственной системы (технической или экономической). Модели, которые строятся с этой целью, называются оптимизационными.
6. Обучение (студентов, персонала и т.п.).
С точки зрения характера получаемой модели различают следующие основные виды моделирования:
1. Вербальное моделирование производится на основе обычного человеческого языка. Вербальная модель – это просто словесное описание оригинала.
2. Графическое моделирование – это представление модели в виде некоего изображения. Например, географическая карта является графической моделью земной поверхности; чертеж детали является ее графической моделью; структурная схема административного устройства организации (учреждения, фирмы и др.) является графической моделью этой организации, на основе которой можно, например, изучать и совершенствовать процедуры документооборота или принятия решений. Вербальные и графические модели широко используются при обучении.
3. Натурное моделирование, при котором оригинал заменяется своим физическим подобием (макетом). Такие модели также используются в обучении (примером могут служить наглядные пособия в учебных лабораториях; натурными моделями являются также всевозможные тренажеры для обучения шоферов, пилотов, операторов сложных производственных систем и др.). Макетами пользуются и при разработке некоторых технических систем (например, при разработке новых самолетов или автомобилей их макеты сначала обдувают воздухом в аэродинамических трубах для выбора обтекаемой формы корпуса).
4. Математическое моделирование основано на использовании математического аппарата. Существует большое количество разновидностей математических моделей, которые в последнее время объединяют общим наименованием – информационные модели. По характеру зависимости от времени математические модели делятся на статические модели, характеристики которых не изменяются во времени и динамические – с переменными во времени характеристиками.
Экономические процессы всегда развиваются во времени. Статической экономическая модель получается, если все ее характеристики отнести к одному и тому же моменту времени. Динамические модели в экономике, в свою очередь, делятся на дискретные и непрерывные. В дискретных моделях изменение параметров связано только с отдельными моментами времени. В непрерывных моделях параметры изменяются во времени плавно.
Математическое описание системы-оригинала может быть получено разными способами.
При теоретическом моделировании система описывается набором уравнений, которые получаются на базе основных законов природы (при моделировании природных и технических систем), а также здравого смысла, человеческого опыта или более или менее обоснованных логически предположений (гипотез) о процессах, происходящих в системе. Именно такие умозрительные предположения часто используются при теоретическом моделировании экономических и социальных систем.
При эмпирическом моделировании формулы и функции, описывающие те или иные стороны поведения системы, получаются путем прямого измерения характеристик системы и обработки полученных экспериментальных данных. В экономических и социальных системах аналогами экспериментальных исследований являются различные статистические обследования.
Важнейшими свойствами моделей являются их полнота, адекватность и точность. Полнота характеризуется тем, какое количество характеристик оригинала отображает модель. Любая модель неполна по сравнению с оригиналом и какие-то характеристики при моделировании "теряются". Однако эти потерянные характеристики могут быть несущественными с точки зрения целей моделирования, а попытка их учесть путем дополнения модели только усложнит ее и затруднит исследование. Уровень полноты модели влияет на ее адекватность. Адекватность – это соответствие, совпадение каких-либо параметров, удовлетворительное с точки зрения определенных целей, т.е. способна дать ответ на поставленные разработчиком вопросы. Точность характеризуется разностью между фактическими и расчетными значениями исследуемого показателя.
Социально-экономические системы относятся, как правило, к так называемым сложным системам. Сложные системы в экономике обладают рядом свойств, которые необходимо учитывать при их моделировании, иначе невозможно говорить об адекватности построенной экономической модели.
Важнейшие свойства сложных систем:
1. Эмерджентность как проявление в наиболее яркой форме свойства целостности системы, т. е. наличие у экономической системы таких свойств, которые не присущи ни одному из составляющих систему элементов, взятому в отдельности, вне системы. Эмерджентность есть результат возникновения между элементами системы так называемых синергических связей, которые обеспечивают увеличение общего эффекта до величины, большей, чем сумма эффектов элементов системы, действующих независимо. Поэтому социально-экономические системы необходимо исследовать и моделировать в целом.
2. Массовый характер экономических явлений и процессов. Закономерности экономических процессов не обнаруживаются на основании небольшого числа наблюдений. Поэтому моделирование в экономике должно опираться на массовые наблюдения.
3. Динамичность экономических процессов, заключающаяся в изменении параметров и структуры экономических систем под влиянием среды (внешних факторов).
4. Случайность и неопределенность в развитии экономических явлений. Поэтому экономические явления и процессы носят в основном вероятностный характер, и для их изучения необходимо применение экономико-математических моделей на базе теории вероятностей и математической статистики.
5. Открытость систем, участвующих в экономической системе. Их невозможно изолировать от окружающей среды, чтобы наблюдать и исследовать их в чистом виде.
6. Активная реакция на появляющиеся новые факторы, последствия которой не всегда предсказуемы.
Выделенные свойства социально-экономических систем осложняют процесс их моделирования, однако эти свойства следует постоянно иметь в виду при рассмотрении различных аспектов экономико-математического моделирования, начиная с выбора типа модели и заканчивая вопросами практического использования результатов моделирования.
Процесс моделирования, в том числе и экономико-математического, включает в себя три структурных элемента:
- объект исследования;
- субъект (исследователь);
- модель, опосредующую отношения между познающим субъектом и познаваемым объектом.
Этапы моделирования:
1 этап: необходимо изучить оригинал: его свойства, систему и подсистемы, входящие в нее, взаимодействие с внешней средой и т. д., из которых отобрать определяющие (основные) составляющие и свойства объекта, определить возможность качественной и количественной их оценки. Выбрать метод моделирования и на основе отобранных переменных построить модель. Познавательные возможности модели определяются тем, что модель отображает лишь некоторые существенные черты исходного объекта, поэтому любая модель замещает оригинал в строго ограниченном смысле. Из этого следует, что для одного объекта может быть построено несколько моделей, отражающих определенные стороны исследуемого объекта или характеризующих его с разной степенью детализации.
2 этап процесса моделирования модель выступает как самостоятельный объект исследования. Одну из форм такого исследования составляет проведение модельных экспериментов, при которых целенаправленно изменяются условия функционирования модели и систематизируются данные о ее «поведении». Конечным результатом этого этапа является совокупность знаний о модели в отношении существенных сторон объекта-оригинала, которые отражены в данной модели.
3 этап заключается в переносе знаний с модели на оригинал, в результате чего формируется множество знаний об исходном объекте и осуществляется переход с языка модели на язык оригинала. С достаточным основанием переносить какой-либо результат с модели на оригинал можно лишь в том случае, если этот результат соответствует признакам сходства оригинала и модели (признакам адекватности).
4 этап: осуществляются практическая проверка полученных с помощью модели знаний и их использование для построения обобщающей теории реального объекта и для его целенаправленного преобразования или управления им. В итоге происходит возврат к проблематике объекта-оригинала.
Моделирование представляет собой циклический процесс: за первым четырехэтапным циклом может последовать второй, третий и т. д. При этом знания об исследуемом объекте расширяются и уточняются, а первоначально построенная модель постепенно совершенствуется. Таким образом, в методологии моделирования заложены большие возможности самосовершенствования.
Перейдем теперь непосредственно к процессу экономико-математического моделирования, т. е. описания экономических и социальных систем и процессов в виде экономико-математических моделей. Эта разновидность моделирования обладает рядом существенных особенностей, связанных как с объектом моделирования, так и с применяемыми аппаратом и средствами моделирования. Поэтому целесообразно более детально проанализировать последовательность и содержание этапов экономико-математического моделирования, выделив следующие шесть этапов:
1. Постановка экономической проблемы и ее качественный анализ. На этом этапе требуется сформулировать сущность проблемы, принимаемые предпосылки и допущения. Необходимо выделить важнейшие черты и свойства моделируемого объекта, изучить его структуру и взаимосвязь его элементов, хотя бы предварительно сформулировать гипотезы, объясняющие поведение и развитие объекта.
2. Построение математической модели. Это этап формализации экономической проблемы, т. е. выражения ее в виде конкретных математических зависимостей (функций, уравнений, неравенств и др.). Построение модели подразделяется в свою очередь на несколько стадий. Сначала определяется тип экономико-математической модели, изучаются возможности ее применения в данной задаче, уточняются конкретный перечень переменных и параметров и форма связей. Для некоторых сложных объектов целесообразно строить несколько разноаспектных моделей; при этом каждая модель выделяет лишь некоторые стороны объекта, а другие стороны учитываются агрегировано и приближенно. Оправдано стремление построить модель, относящуюся к хорошо изученному классу математических задач, что может потребовать некоторого упрощения исходных предпосылок модели, не искажающего основных черт моделируемого объекта. Однако возможна и такая ситуация, когда формализация проблемы приводит к неизвестной ранее математической структуре.
3. Математический анализ модели. На этом этапе чисто математическими приемами исследования выявляются общие свойства модели и ее решений. В частности, важным моментом является доказательство существования решения сформулированной задачи. При аналитическом исследовании выясняется, единственно ли решение, какие переменные могут входить в решение, в каких пределах они изменяются, каковы тенденции их изменения и т. д. Однако модели сложных экономических объектов с большим трудом поддаются аналитическому исследованию; в таких случаях переходят к численным методам исследования.
4. Подготовка исходной информации. В экономических задачах это, как правило, наиболее трудоемкий этап моделирования, так как дело не сводится к пассивному сбору данных. Математическое моделирование предъявляет жесткие требования к системе информации; при этом надо принимать во внимание не только принципиальную возможность подготовки информации требуемого качества, но и затраты на подготовку информационных массивов. В процессе подготовки информации используются методы теории вероятностей, теоретической и математической статистики для организации выборочных обследований, оценки достоверности данных и т.д. При системном экономико-математическом моделировании результаты функционирования одних моделей служат исходной информацией для других.
5. Численное решение. Этот этап включает разработку алгоритмов численного решения задачи, выбор программного обеспечения и непосредственное проведение расчетов, при этом значительные трудности вызываются большой размерностью экономических задач. Обычно расчеты на основе экономико-математической модели носят многовариантный характер. Численное решение существенно дополняет результаты аналитического исследования, а для многих моделей является единственно возможным.
6. Анализ численных результатов и их применение. На этом этапе, прежде всего, решается важнейший вопрос о правильности и полноте результатов моделирования и применимости их как в практической деятельности, так и в целях усовершенствования модели. Поэтому в первую очередь должна быть проведена проверка адекватности модели по тем свойствам, которые выбраны в качестве существенных (другими словами, должны быть произведены верификация и валидация модели). Применение численных результатов моделирования в экономике направлено на решение практических задач (анализ экономических объектов, экономическое прогнозирование развития хозяйственных и социальных процессов, выработка управленческих решений на всех уровнях хозяйственной иерархии).
Перечисленные этапы экономико-математического моделирования находятся в тесной взаимосвязи, в частности, могут иметь место возвратные связи этапов. Так, на этапе построения модели может выясниться, что постановка задачи или противоречива, или приводит к слишком сложной математической модели; в этом случае исходная постановка задачи должна быть скорректирована. Наиболее часто необходимость возврата к предшествующим этапам моделирования возникает на этапе подготовки исходной информации. Если необходимая информация отсутствует или затраты на ее подготовку слишком велики, приходится возвращаться к этапам постановки задачи и ее формализации, чтобы приспособиться к доступной исследователю информации.
Основные понятия оптимизационных моделей
Оптимизационные модели направлены на поиск наилучшего варианта решения из некоторого множества возможных решений. Критерием оптимальности в таких моделях служит достижение экстремального (максимального или минимального) значения некоторой величины, зависящей от переменных модели. Такая величина называется целевой функцией (ЦФ) задачи. Смысл целевой функции зависит от вида и смысла решаемой задачи. В экономических моделях в качестве целевой функции часто выступает прибыль, выручка от реализации выпущенной продукции и т.п. (они в итоге должны оказаться максимальными), или, например, величина производственных издержек (соответственно, в оптимальном случае она должна быть минимальной).
Таким образом, решение задачи оптимизационного моделирования (коротко – «задачи оптимизации») сводится к поиску экстремума некоторой функции.
Различают условные и безусловные задачи оптимизации. В условных задачах на переменные модели накладываются какие-то ограничения, сужающие область определения целевой функции. Простейшим ограничением является естественное для многих практических задач требование неотрицательности переменных, носящих материальный характер (например, объемов выпуска какой-либо продукции, и т.п.). Возможны и другие ограничения, связанные, например, с ограниченностью материальных или финансовых ресурсов. Такие ограничения всегда имеют вид каких-то равенств или неравенств.
В безусловных задачах оптимизации ограничения отсутствуют. Из этого ясно, что экономические задачи оптимизации, как правило, являются условными.
Задачи оптимизации различаются также:
1. По числу переменных:
а) одномерные – целевая функция зависит от одной переменной;
б) многомерные (двумерные, трехмерные и т.д.) – целевая функция зависит от нескольких переменных.
2. По математической структуре:
а) линейные (все математические выражения в задаче имеют вид линейных форм);
б) нелинейные.
Многомерные условные линейные задачи оптимизации называются задачами линейного программирования (ЗЛП).
Практическое занятие 1
Темы докладов:
1. Социально-экономическая система как объект математического моделирования.
2. Задачи и этапы построения математических моделей социально-экономических процессов.
3. Экономико-математическое моделирование в сфере управления различных уровней хозяйствования.
Вопросы для обсуждения:
1. Что такое модель системы?
2. Каковы основные цели, преследуемые при моделировании различных систем?
3. Какие модели называются оптимизационными?
4. Что такое вербальная модель системы?
5. К какому виду моделей относится структурная схема административного устройства организации?
6. В чем состоит разница между теоретическими и эмпирическими моделями?
7. В чем состоит разница между статическими и динамическими моделями?
8. Чем характеризуется полнота модели?
9. Как соотносятся между собой адекватность и точность модели? В каком случае модель с невысокой точностью может считаться адекватной?
10. Что понимается под смешанной (полуэмпирической) моделью системы?
11. Какое действие называется экстраполированием модели? Почему опасно экстраполировать эмпирические модели?
12. Какие действия входят в состав этапа постановки задачи при создании модели системы?
13. Какие действия входят в состав этапа формализации при создании модели системы?
14. Охарактеризуйте понятия точного, приближенного и численного решения математической задачи.
15. Что называется целевой функцией оптимизационной задачи?
16. Что понимается под условной задачей оптимизации?
Практическое занятие 2
Подготовьте доклады по темам:
1. Классификация математических моделей процессов управления.
2. Сравнение словесных и математических моделей.
3. Модели процессов управления предприятием.
4. Модели процессов управления качеством.
5. Макроэкономические модели управления.
6. Соотношение задач, моделей, методов и условий применимости.
7. Место принципа максимума Понтрягина среди математических методов оптимального управления.
Практическое занятие 3
Выучить определения и этапы построения экономико-математической модели задачи.
Решите задачи.
1. Постройте экономико-математическую модель определения суточного рациона, содержащего не менее суточной потребности человека в необходимых питательных веществах и обеспечивающего минимальную общую стоимость продуктов. Для поддержания нормальной жизнедеятельности человеку ежедневно необходимо потреблять 118 г белков, 56 г жиров, 500 г углеводов, 8 г минеральных солей. Количество питательных веществ, содержащихся в 1 кг имеющихся в магазине продуктов питания, а также их стоимость приведены в таблице:
| Питательные вещества | Содержание питательных веществ в 1 кг продуктов | Норма суточной потребности | ||||||
| Мясо | Рыба | Молоко | Масло | Сыр | Крупа | Картофель | ||
| Белки, г | 180 | 190 | 30 | 70 | 260 | 130 | 21 | 118 |
| Жиры, г | 20 | 3 | 40 | 865 | 310 | 30 | 2 | 56 |
| Углеводы, г | 0 | 0 | 50 | 6 | 20 | 650 | 200 | 500 |
| Минеральные соли, г | 9 | 10 | 7 | 12 | 60 | 20 | 70 | 8 |
| Стоимость 1 кг продукта, руб. | 200 | 80 | 28 | 90 | 170 | 30 | 15 | |
Построить экономико-математическую модель задачи.
2. Построить экономико-математическую модель для определения оптимального плана объемов перевозок по следующим условиям. На четырех складах имеется продукция в количестве: А1=200, А2=300, А3=250, А4=180. Для пяти магазинов требуется продукция в количестве: В1=150, В2=100, В3=200, В4=220, В5=210. Стоимость перевозок единицы продукции из i-го склада в j-ый магазин представлены в виде матрицы: 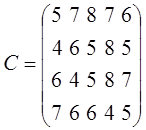 .
.
Домашнее задание:
На складах А1, А2, А3 имеются запасы цемента в 170, 320, 260 тонн соответственно. Получатели груза В1, В2, В3 соответственно должны получить товары в количествах 290, 360 и 100 тонн соответственно. Найти такой вариант перевозки груза, при котором сумма затрат будет минимальной. Расходы перевозки в таблице:
| Грузополучатель | Склад А1 | Склад А2 | Склад А3 |
| В1 | 2,27 | 5,9 | 2,33 |
| В2 | 4,7 | 1,99 | 5,73 |
| В3 | 3,28 | 6,11 | 8,01 |
Построить экономико-математическую модель задачи.
Практическое занятие 4
Выучить алгоритм графического метода.
Решить задачи:
1. Постройте на плоскости X1OX2 область решений системы линейных неравенств и найдите максимальное и минимальное значения линейной функции в этой области:
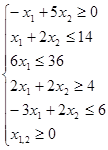 ,
, 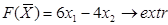
2. Найдите вариант приготовления морса клубничного и морса брусничного, который обеспечивает максимальный доход от продажи, если имеется 5 т смеси 1-го вида и 30 т смеси 2-го вида. На изготовление клубничного идет 60% смеси 1-го вида и 40% смеси 2-го вида, на изготовление морса брусничного идет 80% смеси 1-го вида и 20% смеси 2-го вида. Реализуется 1 л морса клубничного за 50 руб., а 1 л морса брусничного за 60 руб. Задачу решите графическим методом.
3. Фирма производит два сорта хлеба Пшеничный 1 сорта и Пшеничный 2 сорта. Для производства 1 буханки Пшеничного 1 сорта требуется 0,02 ч работы оборудования, а для Пшеничного 2 сорта - 0,04 ч, а теста на них составляет 0,6 кг и 0,5 кг на 1 буханку соответственно. Ежедневно в распоряжении фирмы 160 кг теста и 24 ч работы оборудования. Доход от реализации 1 буханки хлеба Пшеничного 1 сорта составляет 35 руб., а хлеба Пшеничный 2 сорта - 25 руб.
Определите ежедневный план производства хлеба каждого сорта, обеспечивающий максимальный доход от их продажи. Задачу решите графическим методом.
Домашнее задание:
1. Постройте на плоскости X1OX2 область решений системы линейных неравенств и найдите максимальное и минимальное значения линейной функции в этой области:
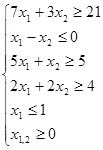 ,
, 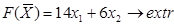
2. Туристическая фирма в летний период обслуживает в среднем 7500 туристов и располагает автобусами двух типов, характеристики которых представлены в таблице:
| Показатели | Автобус | |
| I | II | |
| Пассажировместимость, чел. | 50 | 40 |
| Горючее, т | 120 | 70 |
| Экипаж, чел. | 3 | 2 |
В месяц выделяется 6000 т горючего. Потребность в рабочей силе не превышает 210 человек.
Определите количество автобусов каждого типа, чтобы обеспечить максимальный доход, который составляет от эксплуатации автобуса I типа 2 тыс. руб., II – 1 млн. руб. в месяц. Решите задачу графическим методом.
Практическое занятие 5
Выучите алгоритм симплексного метода.
Решите задачи симплексным методом.
1. На кондитерскую фабрику перед Новым годом поступили заказы на подарочные наборы конфет из трех магазинов. Возможные варианты наборов, их стоимость и товарные запасы на фабрике представлены в таблице:
| Наименование конфет | Вес конфет в наборе, кг | Запасы конфет, кг | ||
| А | В | С | ||
| Сникерс | 0,3 | 0,2 | 0,4 | 600 |
| Марс | 0,2 | 0,3 | 0,2 | 700 |
| Баунти | 0,2 | 0,1 | 0,1 | 500 |
| Цена, руб. | 72 | 62 | 76 | |
Определить оптимальное соотношение количества подарочных наборов, которые фабрика может предложить магазинам и обеспечить максимальный доход от продажи.
2. Фирма выпускает пластиковые пупсы, машинки и совки. В таблице приведены расход продуктов, суточное наличие на складе:
| Исходный продукт | Расход продуктов на 1 шт продукции | Запас на складе | ||
| пупс | машинка | совок | ||
| Пластмасса (кг) | 0,45 | 0,75 | 0,23 | 1000 |
| Затвердитель (г) | 16 | 14 | 12 | 1200 |
| Трудовые затраты (час) | 0,75 | 0,95 | 0,12 | 448 |
Суточный спрос на пупсов на 109 шт. выше, чем на машинки, а на совки на 14 шт. меньше, чем на машинки. Спрос на пупсов не более 130 штук. Отпускная цена пупса – 35 руб., машинки – 49 руб, совка – 5 руб.
3. Фирма выпускает бородинский, галицкий и рижский хлеб. В таблице приведены расход продуктов, суточное наличие запасов на складе:
| Исходный продукт | Расход продуктов на 1 шт продукции | Запас на складе | ||
| бородинский | галицкий | рижский | ||
| Мука( кг) | 0,45 | 0,39 | 0,55 | 1000 |
| Дрожжи (гр) | 16 | 14 | 12 | 1200 |
| молоко | 0,25 | 0,24 | 0,22 | 350 |
Суточный спрос на бородинский на 100 шт выше, чем на рижский, а на галицкий на 44 шт больше, чем на рижский. Спрос на бородинский не более 330 штук. Отпускная цена бородинского – 25 руб, галицкого – 19 руб, рижского– 27 руб. за буханку.
Домашнее задание:
Конкуренция приводит к необходимости торговым предприятиям заниматься еще и выпуском продукции собственного производства, например, пиццы. Нормы затрат на производство пиццы разных видов, объемы ресурсов и стоимость приведены в таблице:
| Продукты | Нормы затрат на изготовление 100 шт. пиццы, кг | Запасы продуктов, кг | ||
| ассорти | грибная | салями | ||
| Грибы | 6 | 7 | 2 | 20 |
| Колбаса | 5 | 2 | 8 | 18 |
| Тесто | 10 | 8 | 6 | 25 |
| Цена за 100 шт., тыс. руб. | 9 | 6 | 5 | |
Определите структуру выпуска пиццы разных видов для получения максимального дохода предприятия.
Практическое занятие 6
Выучите алгоритм двойственного симплексного метода.
Решите задачи двойственным методом.
1. 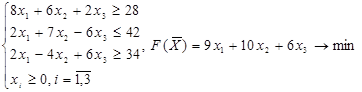
2. 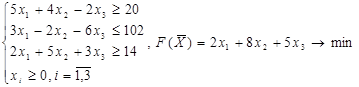
3. Постройте экономико-математическую модель определения структуры блюд на предприятии общественного питания, обеспечивающую максимальный доход на основе заданных нормативов затрат продуктов на первые и вторые блюда, представленных в таблице, и решите ее двойственным симплексным методом.
| Ресурсы | Плановый фонд ресурсов | Нормативные затраты на 100 блюд | ||||
| 1-е блюда | 2-е блюда мясные | 2-е блюда рыбные | 2-е блюда молочные | 2-е блюда прочие | ||
| Мясо, кг | 40000 | 4,0 | 8,0 | - | - | 3,8 |
| Рыба, кг | 25000 | 2,5 | - | 10 | - | - |
| Овощи, кг | 27000 | 3,2 | 2,0 | 3,0 | - | 4,6 |
| Мука, крупа, макаронные изделия, кг | 20000 | 2,1 | 2,6 | 2,3 | 3,2 | 2,8 |
| Молоко, л | 50000 | 6,5 | - | - | 21 | - |
| Доход, руб. | 1,3 | 2,0 | 1,5 | 0,3 | 1,7 | |
Домашнее задание:
Решить задачу двойственным методом:
1. 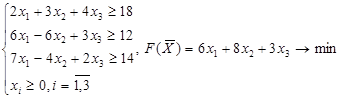
2. По предписанию врача пациенту необходимо перейти на диету для похудения и употреблять питательных веществ, содержащихся в продуктах, в количестве, указанном в таблице:
| Вещества | Содержание питательных веществ в 1 кг фруктов и ягод, г | Нормы потребления, г | ||
| Мясо | Рыба | Овощи | ||
| Белки | 250 | 180 | 10 | 140 |
| Жиры | 120 | 100 | 0 | 30 |
| Углеводы | 40 | 80 | 140 | 200 |
| Цена за 1 кг, руб. | 220,0 | 100,0 | 35,0 | |
Определить оптимальный план употребления продуктов с минимальными затратами.
Практическое занятие 7
Выучить правила перехода от прямой задачи к двойственной.
Решить задачи.
1. Записать математическую модель двойственной задачи линейного программирования по заданной прямой задаче:
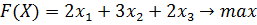 ,
,
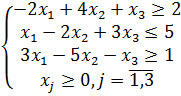
2. Для производства трех изделий А, В и С используются три вида сырья. Каждый из них используется в объеме, не превышающем 180, 210 и 236 кг. Нормы затрат каждого из видов сырья на одно изделие и цена единицы изделий приведены в таблице.
| Вид сырья | Нормы затрат сырья на одно изделие, кг | ||
| А | В | С | |
| 1 | 4 | 2 | 1 |
| 2 | 3 | 1 | 3 |
| 3 | 1 | 2 | 5 |
| Цена изделия, тыс. руб. | 10 | 14 | 12 |
Определить план выпуска изделий, обеспечивающий получение максимального дохода. Составить для данной задачи двойственную и найти оптимальный план двойственной задачи.
Домашнее задание:
Найти решение задачи:
1. 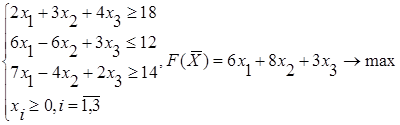
Транспортная задача
Транспортная задача – это задача об оптимальном плане перевозок товаров из пунктов отправления в пункты потребления. Целью транспортной задачи является доставка товаров в определенное время и место при минимальных совокупных затратах трудовых, материальных и финансовых ресурсов или времени доставки.
Выделяют два типа транспортных задач по критерию оптимальности:
- по критерию стоимости – план перевозок является оптимальным, если достигается минимум затрат на его реализацию;
- по критерию времени – план перевозок оптимален, если на него затрачивается минимальное количество времени.
В общем виде задачу можно представить следующим образом: в m пунктах отправления А1, А2, ... , Аm имеется однородный груз в количестве соответственно а1, а2, ... , аm. Этот груз необходимо доставить в n пунктов потребления В1, В2, ... , Вn в количестве соответственно b1, b2, ... , bn. Стоимость перевозки единицы груза (тариф) из пункта Ai в пункт Bj равна сij. Требуется составить такой план перевозок, который позволит вывезти весь товар и имеющий минимальную стоимость (минимальное время перевозки). В зависимости от соотношения между суммарными запасами товара и суммарными потребностями в нем транспортные задачи могут быть закрытыми и открытыми.
Задача называется закрытой, если сумма товара на всех пунктах отправления равна сумме потребностей в товаре на всех пунктах назначения, то есть 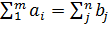 ,
,
Если сумма товара на всех пунктах отправления не равна сумме потребностей в товаре на всех пунктах назначения, то есть 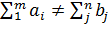 , то задача называется открытой.
, то задача называется открытой.
Обозначим через x ij количество груза, перевозимого из пункта Ai в пункт Bj. Рассмотрим транспортную задачу закрытого типа.
Математическая модель транспортной задачи имеет вид:
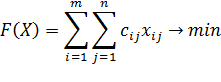
при ограничениях:
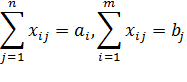
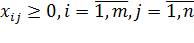 .
.
Оптимальным решением задачи является матрица
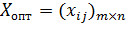 ,
,
удовлетворяющая системе ограничений и обеспечивающая минимальное значение целевой функции.
Алгоритм транспортной задачи
1) Нахождение исходного опорного решения. Данные задачи записываем в таблицу:
|
| bj | b1 | b2 | … | br | … | bn | |||||
| ai |
| |||||||||||
| a1 | x11 | c11 | x12 | c12 | … | x1r | c1r | … | x1n | c1n | ||
| a2 | x21 | c21 | x22 | c22 | … | x2r | c2r | … | x2n | c2n | ||
| … | … | … | … | … | … | … | ||||||
| ak | xk1 | ck1 | xk2 | ck2 | … | xkr | ckr | … | xkn | ckn | ||
| … | … | … | … | … | … | … | ||||||
| am | xm1 | cm1 | xm2 | cm2 | … | xmr | cmr | … | xmn | cmn | ||
Распределение x ij можно проводить с помощью метода минимального элемента. Для этого из всех стоимостей выбираем наименьшую и в эту ячейку записываем меньшее значение из соответствующих значений 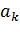 и
и 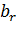 . Если записывается значение пункта отправления, то все оставшиеся ячейки данной строки заполняются знаками ×, если в указанную ячейку заполняется значение пункта потребления, то все оставшиеся ячейки соответствующего столбца заполняются знаками ×. Эти ячейки считаются заполненными. Если ячеек с наименьшей стоимостью несколько, то сначала заполняем ту ячейку, в которую можно записать большее значение.
. Если записывается значение пункта отправления, то все оставшиеся ячейки данной строки заполняются знаками ×, если в указанную ячейку заполняется значение пункта потребления, то все оставшиеся ячейки соответствующего столбца заполняются знаками ×. Эти ячейки считаются заполненными. Если ячеек с наименьшей стоимостью несколько, то сначала заполняем ту ячейку, в которую можно записать большее значение.
Далее из оставшихся незаполненных ячеек снова выбираем наименьшую стоимость и заполняем ячейки аналогично вышеописанному действию. И так заполняем ячейки до тех пор, пока не будут заполнены все ячейки. После того, как все ячейки заполнены необходимо проверить, соответствуют ли значение пунктов отправления суммам по соответствующим строкам, и значения пунктов потребления суммам по соответствующим столбцам.
|
| bj | b1 | b2 | … | br | … | bn |
| ||||
| ai |
| |||||||||||
| a1 | x11 | c11 | x12 | c12 | … | x1r | c1r | … | x1n | c1n | 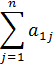
| |
| a2 | x21 | c21 | x22 | c22 | … | x2r | c2r | … | x2n | c2n | 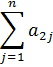
| |
| … | … | … | … | … | … | … | … | |||||
| ak | xk1 | ck1 | xk2 | ck2 | … | xkr | ckr | … | xkn | ckn | 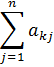
| |
| … | … | … | … | … | … | … | … | |||||
| am | xm1 | cm1 | xm2 | cm2 | … | xmr | cmr | … | xmn | cmn | 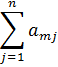
| |
|
|
| … |
| … |
| |||||||
При распределении товара по клеткам может оказаться, что количество занятых клеток меньше, чем m + n – 1 (m – количество пунктов отправления, n – количество пунктов назначения). Такой план называется вырожденным. В этом случае недостающее их число заполняется клетками с нулевыми поставками, такие клетки называют условно занятыми. Нулевые поставки помещают в пустые клетки с учетом наименьшей стоимости перевозки таким образом, чтобы в каждых строке и столбце было не менее чем по одной занятой клетке.
2) Проверка плана на оптимальность.
Проверить план на оптимальность можно с помощью метода потенциалов. Для этого к таблице опорного решения добавим столбец 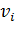 и строку
и строку 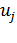 . Числа
. Числа 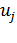 и
и 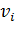 называют потенциалами. Рассчитываются потенциалы для занятых клеток по равенству
называют потенциалами. Рассчитываются потенциалы для занятых клеток по равенству 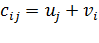 . Любому потенциалу сначала придаем значение любое значение (удобнее придать нулевое значение потенциалу
. Любому потенциалу сначала придаем значение любое значение (удобнее придать нулевое значение потенциалу 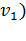 .
.
|
| bj | b1 | b2 | … | br | … | bn |
| ||||
| ai |
| |||||||||||
| a1 | x11 | c11 | x12 | c12 | … | x1r | c1r | … | x1n | c1n | 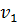
| |
| a2 | x21 | c21 | x22 | c22 | … | x2r | c2r | … | x2n | c2n | 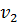
| |
| … | … | … | … | … | … | … | … | |||||
| ak | xk1 | ck1 | xk2 | ck2 | … | xkr | ckr | … | xkn | ckn | 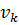
| |
| … | … | … | … | … | … | … | … | |||||
| am | xm1 | cm1 | xm2 | cm2 | … | xmr | cmr | … | xmn | cmn | 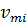
| |
|
|
|
| … |
| … |
| ||||||
Для всех свободных клеток рассчитаем напряженности, которые показывают возможность уменьшения цены. Напряженности рассчитываются по формуле: 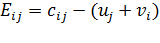 . Критерием оптимальности плана является отсутствие отрицательных напряженностей, то есть
. Критерием оптимальности плана является отсутствие отрицательных напряженностей, то есть 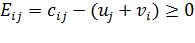 . Если есть хотя бы одна отрицательная напряженность, то план неоптимальный и его можно улучшить.
. Если есть хотя бы одна отрицательная напряженность, то план неоптимальный и его можно улучшить.
3) Переход от одного опорного решения к другому.
Переход от одного плана к другому осуществляется по циклу.
Цикл – замкнутая ломаная линия, состоящая из горизонтальных и вертикальных ребер, вершинами которой являются только заполненные ячейки, за исключением начала цикла. Цикл может иметь любую форму (примеры на рисунке 1.7).

Рис. 1.7. Примеры форм циклов
Начало цикла соответствует ячейке, у которой наибольшее по абсолютной величине отрицательное значение напряженности 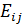 . Если таких ячеек несколько, то выбирается та ячейка, которой соответствует меньшая цена. Далее от начала цикла методом подбора по заполненным ячейкам составляем ребра цикла до тех пор, пока не вернемся в начало цикла. Цикл единственный.
. Если таких ячеек несколько, то выбирается та ячейка, которой соответствует меньшая цена. Далее от начала цикла методом подбора по заполненным ячейкам составляем ребра цикла до тех пор, пока не вернемся в начало цикла. Цикл единственный.
В начало цикла ставим (+), далее чередуем (-), (+) и т. д. Направление движения для чередования может быть любым.
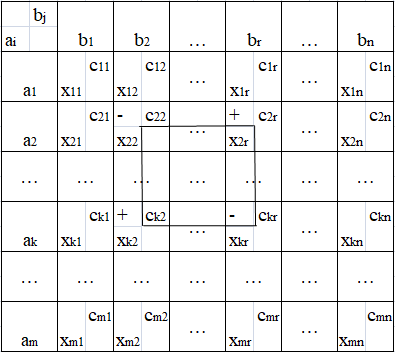
Из всех вершин цикла за знаком (-) выбираем наименьшее и в новом плане к ячейкам со знаком (+) прибавляем, а от ячеек со знаком (-) отнимаем. Остальные значения плана переписываем из предыдущего.
4) Проверяем план на оптимальность (п.2 алгоритма).
Пункты 2 – 4 алгоритма выполняем до тех пор, пока план не будет оптимальным.
При составлении опорного плана и при каждом переходе к новому плану необходимо рассчитывать стоимость перевозки по формуле
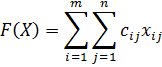
Значение стоимости перевозки с каждым переходом к новому плану должно уменьшаться. Если уменьшения не произошло, значит, была допущена ошибка.
Пример. Три фермерских хозяйства поставляют огурцы четырем оптовым покупателям. Ежедневная потребность покупателей составляет 10, 110, 40 и 110 ц соответственно. Фермерские хозяйства могут ежедневно поставлять 60, 120 и 100 ц огурцов соответственно. Матрица стоимостей перевозки 1 ц огурцов имеет вид 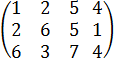 . Найти оптимальный план поставки огурцов.
. Найти оптимальный план поставки огурцов.
Решение.
1) Найдем опорный план, используя метод минимального элемента.
Проверим задачу на открытость.
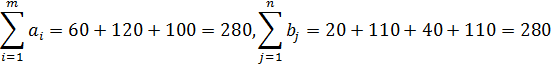
Следовательно, задача закрытая.
|
| 280 | 20 | 110 | 40 | 110 |
| ||||
| 280 |
| |||||||||
| 60 | 20 | 1 | 40 | 2 | х | 5 | х | 4 | 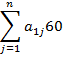
| |
| 120 | х | 2 | х | 6 | 10 | 5 | 110 | 1 | 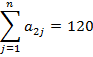
| |
| 100 | х | 6 | 70 | 3 | 30 | 7 | х | 4 | 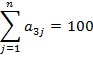
| |
|
|
|
|
| |||||||
Минимальная стоимость равна 1 в двух ячейках. Начинаем заполнять с ячейки, в которую можно записать большее значение, то есть с ячейки с индексом 23. Потребность третьего потребителя удовлетворена полностью, значит оставшиеся ячейки этого столбца заполняем знаком «х». Из оставшихся пустых ячеек выбираем наименьшую стоимость. Это 1. Заполняем соответствующую ячейку. Потребность первого потребителя удовлетворена полностью, значит, оставшиеся ячейки в данном столбце заполняем знаком «х». И так далее.
Заполнив все ячейки, проверим соответствие сумм по строкам и столбцам.
Рассчитаем стоимость перевозки: 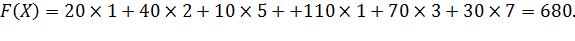
Посчитаем количество заполненных ячеек, их должно быть ровно m + n -1. В нашей таблице 6 заполненных ячеек, что соответствует условию, и задача является невырожденной.
2) Проверим план на оптимальность. Для этого дополним таблицу столбцом и строкой и рассчитаем потенциалы 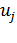 и
и 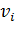 .
.
|
| 280 | 20 | 110 | 40 | 110 |
| ||||
| 280 |
| |||||||||
| 60 | 20 | 1 | 40 | 2 | х | 5 | х | 4 | 0 | |
| 120 | х | 2 | х | 6 | 10 | 5 | 110 | 1 | -1 | |
| 100 | х | 6 | 70 | 3 | 30 | 7 | х | 4 | 1 | |
|
| 1 | 2 | 6 | 2 | ||||||
Теперь рассчитаем напряженности для пустых клеток.
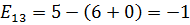 ,
,
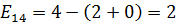 ,
,
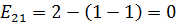 ,
,
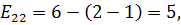
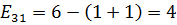 ,
,
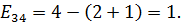
Так как есть отрицательное значение напряженности, то план является неоптимальным и его нужно улучшать.
3) Пересчитаем план.
Начало цикла будет в ячейке с индексов 13.
|
| 280 | 20 | 110 | 40 | 110 |
| ||||
| 280 |
| |||||||||
| 60 | 20 | 1 | -
40 |
| +
х | 5 | х | 4 | 0 | |
| 120 | х | 2 | х | 6 | 10 | 5 | 110 | 1 | -1 | |
| 100 | х | 6 | 70 | 3
+ | 30 | 7
- | х | 4 | 1 | |
|
| 1 | 2 | 6 | 2 | ||||||
Из всех значений в ячейках со знаком (-) выбираем меньшее и в новом плане к ячейкам со знаком (+) прибавляем 30, а от ячеек со знаком (-) отнимаем. Получим новый план.
|
| 280 | 20 | 110 | 40 | 110 |
| ||||
| 280 |
| |||||||||
| 60 | 20 | 1 | 10 | 2 | 30 | 5 | х | 4 | ||
| 120 | х | 2 | х | 6 | 10 | 5 | 110 | 1 | ||
| 100 | х | 6 | 100 | 3 | х | 7 | х | 4 | ||
|
| ||||||||||
Рассчитаем сумму стоимости перевозки. 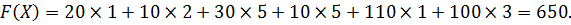 Стоимость перевозки уменьшилась, значит, расчеты проведены верно.
Стоимость перевозки уменьшилась, значит, расчеты проведены верно.
2) Проверим план на оптимальность.
Найдем потенциалы 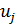 и
и 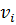 .
.
|
| 280 | 20 | 110 | 40 | 110 |
| ||||
| 280 |
| |||||||||
| 60 | 20 | 1 | 10 | 2 | 30 | 5 | х | 4 | 0 | |
| 120 | х | 2 | х | 6 | 10 | 5 | 110 | 1 | 0 | |
| 100 | х | 6 | 100 | 3 | х | 7 | х | 4 | 1 | |
|
| 1 | 2 | 5 | 1 | ||||||
Рассчитаем напряженности для пустых клеток.
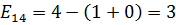 ,
,
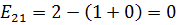 ,
,
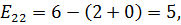
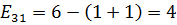 ,
,
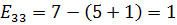 ,
,
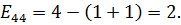
Среди найденных значений напряженностей нет отрицательных, следовательно, план оптимальный.
Ответ: минимальной суммой стоимости перевозки является 650. План перевозки:
Первый фермер поставляет 20 ц огурцов первому потребителю, 10 ц огурцов второму потребителю, 30 ц огурцов третьему потребителю.
Второй фермер поставляет 10 ц третьему потребителю и 110 ц четвертому потребителю.
Третий фермер поставляет 100 ц второму потребителю.
Рассмотрим транспортную задачу открытого типа ( 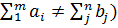 .
.
Решение транспортной задачи открытого типа сводится к решению транспортной задачи закрытого типа путем введения дополнительных (фиктивных) пунктов отправления или назначения с нулевыми стоимостями.
Если сумма имеющего товара в пунктах потребления больше суммы потребностей, то вводится фиктивный потребитель разницы. Если сумма потребностей больше суммы имеющего товара в пунктах отправления, то вводится фиктивный пункт отправления с нулевыми стоимостями. И далее задача решается так же, как задача закрытого типа.
Применение транспортной задачи
Транспортная задача может быть применены во многих социально-экономических областях. Существует множество прикладных социально-экономических задач, которые можно свести к транспортной задаче. Некоторые из таких задач приведены ниже.
Задача оптимального распределения работ. Требуется распределить m работ по n сотрудникам (отделам, участкам) так, чтобы суммарные затраты времени (финансов) были минимальными. Предполагается, что каждый сотрудник (отдел, участок) выполняет одну работу [17].
Задача оптимизации затрат на обучение персонала. Фирма располагает n группами должностей по 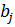 вакантных единиц в каждой группе; кандидаты на занятие должностей проходят тестирование, по результатам которого их разделяют на m групп по
вакантных единиц в каждой группе; кандидаты на занятие должностей проходят тестирование, по результатам которого их разделяют на m групп по 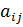 кандидатов в каждой группе; требуются затраты
кандидатов в каждой группе; требуются затраты 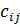 на обучение кандидата i-ой группы для занятия j-ой должности (если
на обучение кандидата i-ой группы для занятия j-ой должности (если 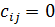 , кандидат полностью соответствует должности и обучение (переподготовка или повышение квалификации) не требуется, если
, кандидат полностью соответствует должности и обучение (переподготовка или повышение квалификации) не требуется, если 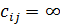 (или
(или 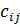 - любое заведомо большое число), кандидат не может занять данную должность). Требуется распределить кандидатов на должности, затратив минимальные средства на их обучение [17].
- любое заведомо большое число), кандидат не может занять данную должность). Требуется распределить кандидатов на должности, затратив минимальные средства на их обучение [17].
Задача оптимального распределения торговых агентов. Необходимо определить план продаж товара в нескольких городах с известной покупательной способностью жителей и известным профессиональным уровнем агентов, чтобы получить максимальный ожидаемый доход от продажи товаров [17].
Задача оптимального размещения производства. Требуется разработать план выпуска n новых видов продукции на m предприятиях при известных издержках производства и сбыта единицы продукции каждого вида, предполагаемом спросе на продукцию каждого вида и прогнозируемой цене за единицу продукции, максимизирующий ожидаемую прибыль [17].
Задача оптимального распределения оборудования. Оборудование различных видов нужно распределить между n рабочими участками так, чтобы суммарная производительность оказалась максимальной (производительность оборудования i -го вида на j-м участке равно 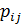 ) [17].
) [17].
Практическое занятие 8
Выучить алгоритм транспортной задачи.
Решить задачи.
1. На складах имеется товар в количестве А1=77, А2=53, А3=120, А4=60. В три магазина требуется товар в количестве В1=80, В2=80, В3=150. Матрица стоимостей 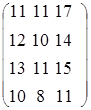 .
.
2. На складах имеется товар в количестве А1=80, А2=80, А3=50, А4=10. В четыре магазина требуется товар в количестве В1=65, В2=65, В3=75, В4=15. Матрица стоимостей 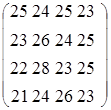 .
.
3. На складах имеется товар в количестве А1=60, А2=55, А3=120, А4=25. В четыре магазина требуется товар в количестве В1=75, В2=85, В3=80, В4=20. Матрица стоимостей 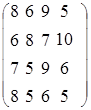 .
.
Домашнее задание:
1. Построить оптимальный план объемов перевозок по следующим условиям. На четырех складах имеется продукция в количестве: А1=200, А2=300, А3=250, А4=180. Для пяти магазинов требуется продукция в количестве: В1=150, В2=100, В3=200, В4=220, В5=210. Стоимость перевозок единицы продукции из i-го склада в j-ый магазин представлены в виде матрицы: 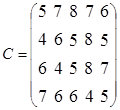 .
.
2. Построить оптимальный план объемов перевозок из трех складов в четыре магазина, если А1=150, А2=200, А3=180, В1=120, В2=100, В3=110, В4=200. Стоимость перевозок представлена в виде матрицы 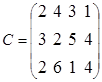 .
.
Задание 2. Решить транспортную задачу.
Имеются 3 пункта поставки однородного груза А1, А2, А3 и 4 пункта потребления этого груза В1, В2, В3, В4. На пунктах А (I = 1,2,3 ) груз находится соответственно в количествах а1, а2, а3 условных единиц. В пункты В ( J= 1,2,3,4) требуется доставить соответственно bj единиц груза. Стоимость перевозки единицы груза (с учетом расстояний) из А, в В указана в таблице. Найти оптимальный план закрепления потребителей и поставщиков, чтобы общие затраты на перевозки были минимальными.
1
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 12 | 15 | 21 | 11 | 240 |
| A2 | 14 | 8 | 15 | 20 | 190 |
| A3 | 19 | 16 | 26 | 19 | 190 |
| Потребности | 140 | 190 | 170 | 120 |
2
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 15 | 21 | 14 | 7 | 350 |
| A2 | 8 | 15 | 11 | 9 | 330 |
| A3 | 16 | 26 | 12 | 13 | 270 |
| Потребности | 160 | 390 | 250 | 150 |
3
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 21 | 14 | 17 | 11 | 290 |
| A2 | 15 | 11 | 21 | 12 | 240 |
| A3 | 26 | 12 | 20 | 13 | 190 |
| Потребности | 200 | 260 | 140 | 120 |
4
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 12 | 21 | 9 | 8 | 450 |
| A2 | 13 | 15 | 11 | 15 | 300 |
| A3 | 19 | 26 | 12 | 13 | 400 |
| Потребности | 340 | 290 | 370 | 150 |
5
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 21 | 9 | 10 | 14 | 180 |
| A2 | 15 | 11 | 13 | 13 | 230 |
| A3 | 26 | 12 | 17 | 21 | 180 |
| Потребности | 220 | 160 | 120 | 90 |
6
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 9 | 10 | 16 | 14 | 340 |
| A2 | 11 | 13 | 21 | 11 | 360 |
| A3 | 12 | 17 | 20 | 21 | 280 |
| Потребности | 260 | 380 | 160 | 180 |
7
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 8 | 12 | 5 | 6 | 230 |
| A2 | 4 | 13 | 12 | 8 | 330 |
| A3 | 16 | 19 | 13 | 10 | 280 |
| Потребности | 190 | 290 | 120 | 240 |
8
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 21 | 10 | 15 | 14 | 300 |
| A2 | 15 | 13 | 21 | 11 | 450 |
| A3 | 26 | 17 | 20 | 25 | 400 |
| Потребности | 360 | 420 | 220 | 150 |
9
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 13 | 8 | 10 | 9 | 190 |
| A2 | 14 | 4 | 13 | 11 | 190 |
| A3 | 20 | 16 | 17 | 13 | 240 |
| Потребности | 100 | 290 | 110 | 120 |
10
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 7 | 11 | 16 | 11 | 340 |
| A2 | 12 | 15 | 17 | 21 | 280 |
| A3 | 11 | 12 | 19 | 13 | 360 |
| Потребности | 390 | 280 | 130 | 180 |
11
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 20 | 8 | 7 | 9 | 250 |
| A2 | 14 | 4 | 12 | 5 | 300 |
| A3 | 22 | 15 | 11 | 14 | 200 |
| Потребности | 290 | 170 | 140 | 150 |
12
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 7 | 11 | 16 | 12 | 440 |
| A2 | 12 | 15 | 17 | 8 | 490 |
| A3 | 11 | 12 | 19 | 9 | 340 |
| Потребности | 300 | 410 | 290 | 270 |
13
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 7 | 22 | 8 | 9 | 310 |
| A2 | 12 | 14 | 4 | 11 | 310 |
| A3 | 11 | 20 | 15 | 21 | 260 |
| Потребности | 230 | 310 | 160 | 180 |
14
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 7 | 12 | 28 | 13 | 320 |
| A2 | 12 | 14 | 35 | 28 | 250 |
| A3 | 11 | 16 | 30 | 17 | 340 |
| Потребности | 260 | 190 | 250 | 210 |
15
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 18 | 7 | 12 | 10 | 450 |
| A2 | 15 | 12 | 14 | 17 | 400 |
| A3 | 25 | 11 | 16 | 21 | 450 |
| Потребности | 270 | 400 | 330 | 300 |
16
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 7 | 18 | 7 | 6 | 330 |
| A2 | 12 | 15 | 3 | 8 | 430 |
| A3 | 11 | 25 | 15 | 11 | 380 |
| Потребности | 330 | 320 | 250 | 240 |
17
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 14 | 6 | 4 | 5 | 320 |
| A2 | 17 | 10 | 9 | 7 | 500 |
| A3 | 15 | 11 | 6 | 12 | 380 |
| Потребности | 240 | 440 | 220 | 300 |
18
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 4 | 4 | 9 | 11 | 230 |
| A2 | 9 | 5 | 11 | 21 | 470 |
| A3 | 6 | 4 | 13 | 3 | 310 |
| Потребности | 270 | 290 | 240 | 210 |
19
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 14 | 6 | 4 | 8 | 260 |
| A2 | 17 | 10 | 9 | 7 | 390 |
| A3 | 15 | 11 | 6 | 14 | 370 |
| Потребности | 240 | 390 | 270 | 120 |
20
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 14 | 4 | 9 | 13 | 320 |
| A2 | 17 | 5 | 11 | 10 | 320 |
| A3 | 15 | 8 | 13 | 9 | 370 |
| Потребности | 270 | 270 | 260 | 210 |
21
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 9 | 15 | 35 | 15 | 370 |
| A2 | 15 | 35 | 12 | 18 | 320 |
| A3 | 16 | 19 | 40 | 9 | 220 |
| Потребности | 350 | 180 | 170 | 210 |
22
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 15 | 35 | 20 | 11 | 280 |
| A2 | 35 | 12 | 11 | 15 | 280 |
| A3 | 19 | 16 | 15 | 10 | 380 |
| Потребности | 190 | 290 | 220 | 240 |
23
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 7 | 20 | 15 | 17 | 320 |
| A2 | 6 | 11 | 35 | 10 | 220 |
| A3 | 25 | 15 | 19 | 21 | 470 |
| Потребности | 250 | 350 | 200 | 210 |
24
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 20 | 3 | 9 | 15 | 330 |
| A2 | 14 | 10 | 12 | 11 | 170 |
| A3 | 25 | 11 | 16 | 8 | 250 |
| Потребности | 270 | 160 | 170 | 150 |
25
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 12 | 9 | 15 | 17 | 240 |
| A2 | 14 | 12 | 20 | 10 | 190 |
| A3 | 19 | 16 | 19 | 11 | 190 |
| Потребности | 140 | 190 | 170 | 120 |
26
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 17 | 18 | 7 | 16 | 430 |
| A2 | 12 | 15 | 13 | 18 | 330 |
| A3 | 11 | 25 | 15 | 16 | 580 |
| Потребности | 430 | 220 | 450 | 340 |
27
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 14 | 16 | 14 | 15 | 230 |
| A2 | 17 | 10 | 19 | 17 | 350 |
| A3 | 16 | 11 | 16 | 12 | 380 |
| Потребности | 240 | 540 | 120 | 300 |
28
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 14 | 14 | 9 | 11 | 230 |
| A2 | 9 | 5 | 11 | 21 | 370 |
| A3 | 6 | 14 | 13 | 13 | 310 |
| Потребности | 370 | 290 | 280 | 210 |
29
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 14 | 16 | 14 | 8 | 360 |
| A2 | 17 | 10 | 9 | 7 | 490 |
| A3 | 15 | 11 | 16 | 14 | 370 |
| Потребности | 440 | 390 | 270 | 520 |
30
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 14 | 14 | 19 | 13 | 320 |
| A2 | 16 | 15 | 11 | 10 | 360 |
| A3 | 15 | 17 | 15 | 19 | 370 |
| Потребности | 270 | 280 | 360 | 210 |
31
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 19 | 15 | 35 | 15 | 470 |
| A2 | 15 | 35 | 12 | 18 | 320 |
| A3 | 16 | 19 | 40 | 19 | 220 |
| Потребности | 350 | 280 | 270 | 310 |
32
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 15 | 25 | 10 | 11 | 480 |
| A2 | 25 | 12 | 11 | 15 | 250 |
| A3 | 19 | 16 | 15 | 10 | 380 |
| Потребности | 290 | 290 | 220 | 240 |
33
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 7 | 20 | 15 | 17 | 120 |
| A2 | 6 | 10 | 15 | 10 | 220 |
| A3 | 15 | 12 | 19 | 21 | 470 |
| Потребности | 250 | 150 | 200 | 210 |
34
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 20 | 13 | 19 | 15 | 230 |
| A2 | 14 | 10 | 12 | 11 | 370 |
| A3 | 25 | 11 | 16 | 18 | 250 |
| Потребности | 270 | 260 | 270 | 250 |
35
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 12 | 19 | 15 | 14 | 240 |
| A2 | 14 | 12 | 20 | 10 | 290 |
| A3 | 14 | 16 | 15 | 11 | 390 |
| Потребности | 240 | 290 | 170 | 220 |
36
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 12 | 15 | 21 | 11 | 240 |
| A2 | 14 | 18 | 15 | 18 | 290 |
| A3 | 19 | 16 | 16 | 19 | 350 |
| Потребности | 240 | 190 | 270 | 220 |
37
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 15 | 21 | 14 | 17 | 320 |
| A2 | 18 | 15 | 11 | 19 | 330 |
| A3 | 16 | 26 | 12 | 13 | 370 |
| Потребности | 260 | 390 | 250 | 250 |
38
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 11 | 14 | 17 | 11 | 190 |
| A2 | 15 | 11 | 11 | 12 | 240 |
| A3 | 16 | 12 | 10 | 13 | 290 |
| Потребности | 100 | 160 | 140 | 120 |
39
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 12 | 11 | 19 | 18 | 350 |
| A2 | 13 | 15 | 11 | 15 | 300 |
| A3 | 19 | 26 | 12 | 13 | 250 |
| Потребности | 240 | 290 | 270 | 150 |
40
| Пункты назнач. |
B1 |
B2 |
B3 |
B4 |
Запасы |
| Пункты Отправ. | |||||
| A1 | 11 | 19 | 10 | 14 | 280 |
| A2 | 15 | 11 | 13 | 13 | 230 |
| A3 | 16 | 12 | 17 | 15 | 250 |
| Потребности | 220 | 260 | 220 | 190 |
Практическое занятие 9
1. Формализуйте (сделайте математическую постановку) следующие задачи:
а) задачу оптимизации затрат на обучение персонала;
б) задачу оптимального распределения торговых агентов;
в) задачу оптимального размещения производства.
2. Предположим, что нам необходимо составить оптимальный суточный рацион кормления на стойловый период для дойных коров. На 1 голову скота в сутки требуется не менее 16,1кг кормовых единиц и 1819г перевариваемого протеина. Рацион составляется из трёх видов кормов: комбикорма, сена, силоса. Содержание питательных веществ в единице каждого вида корма и себестоимость кормов приведены в таблице ниже.
Содержание питательных веществ в 1 кг корма и себестоимость кормов
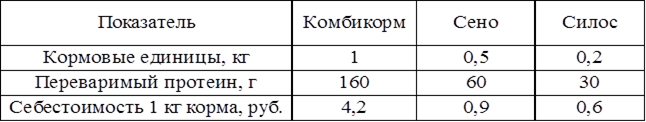
Согласно физиологическим особенностям животных в рационе должно содержаться не менее 31% концентрированных (комбикорм) и не более 26% грубых (сено) кормов от общей потребности в кормовых единицах.
Критерий оптимальности – минимум себестоимости рациона при выполнении условий по необходимому содержанию питательных веществ в рационе.
3. Фабрика выпускает продукцию двух видов: П1 и П2. Продукция обоих видов поступает в оптовую продажу. Для производства этой продукции используются три исходных продукта - А, В, С. Максимально возможные суточные запасы этих продуктов составляют 6, 8 и 5 т соответственно. Расходы сырья А, В, С на 1 тыс. изделий П1 и П2 приведены в таблице.
| Исходный продукт | Расход исходных продуктов на 1 тыс. изделий (т) | Максимально возможный запас (т) | |
| П1 | П2 | ||
| А В С | 1 2 1 | 2 1 0.8 | 6 8 5 |
Изучение рынка сбыта показало, что суточный спрос на изделия П2никогда не превышает спроса на изделия П1 более чем на 1 тыс. шт. Кроме того, установлено, что спрос на изделия П2 никогда не превышает 2 тыс. шт. в сутки.
Оптовые цены 1 тыс. шт. изделий П1 равны 3 тыс. руб., 1 тыс. шт. П2 - 2 тыс. шт. Какое количество изделий (в тыс. шт.) каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?
4. Предприятие производит изделия трех видов, поставляет их заказчикам и реализует на рынке. Заказчикам требуется 1000 изделий первого вида. 2000 изделий второго вида и 2500 изделий третьего вида.
Условия спроса на рынке ограничивают число изделий первого вида 2000 единицами, второго – 3000 и третьего – 5000 единицами.
Для изготовления изделий используется 4 типа ресурсов. Количество ресурсов, потребляемых для производства одного изделия, общее количество ресурсов и прибыль от реализации каждого вида изделия заданы в таблице.
| Тип ресурсов | Вид изделий | Всего ресурсов | ||
| 1 | 2 | 3 | ||
| 1 2 3 4 | 500 1000 150 100 | 300 200 300 200 | 1000 100 200 400 | 25000000 30000000 20000000 40000000 |
| Прибыль | 20 | 40 | 50 | |
Как организовать производство, чтобы:
1) обеспечить заказчиков;
2) не допустить затоваривания;
3) получить максимальную прибыль?
Домашнее задание:
1. При продаже двух видов товара используется 4 типа ресурсов. Норма затрат ресурсов на реализацию единицы товара, общий объем каждого ресурса заданы в табл. 3.2.
Прибыль от реализации одной единицы товара первого вида составляет 2 усл. ед., второго вида – 3 усл. ед.
Требуется найти оптимальный план реализации товаров, обеспечивающий торговому предприятию максимальную прибыль.
| Ресурсы | Норма затрат ресурсов на товары | Общее количество ресурсов | |
| 1 -го вида | 2-го вида | ||
| 1 2 3 4 | 2 1 4 0 | 2 2 0 4 | 12 8 16 12 |
2. Предприятие рекламирует свою продукцию с использованием четырех источников массовой информации: телевидения, радио, газет и расклейки объявлений. Анализ рекламной деятельности в прошлом показал, что эти средства приводят к увеличению прибыли соответственно на 10, 5, 7 и 4 усл. ед., в расчете на 1 усл. ед., затраченную на рекламу. На рекламу выделено 50 000 усл. ед. Администрация предприятия не намерена тратить на телевидение более 40 %, а на радио и газеты — более 50 % от общей суммы выделенных средств. Как следует предприятию организовать рекламу, чтобы получить максимальную прибыль?
Практическое занятие 10
1. Распределить оптимальным образом средства инвестора величиной Х между тремя предприятиями. От выделенной суммы зависит прирост выпуска продукции на предприятиях, значения которого приведены в таблице:
| Денежные средства, Х | Прирост выпуска продукции | ||
| I | II | III | |
| 20 | 10 | 11 | 13 |
| 40 | 17 | 33 | 29 |
| 60 | 28 | 45 | 38 |
| 80 | 38 | 51 | 49 |
| 100 | 46 | 68 | 61 |
| 120 | 68 | 80 | 81 |
2. Планируется распределение начальной суммы 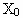 млн. р. Между четырьмя предприятиями некоторого объединения. Средства выделяются только в размерах кратных
млн. р. Между четырьмя предприятиями некоторого объединения. Средства выделяются только в размерах кратных 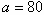 млн. р. Функции прироста продукции от вложенных средств на каждом предприятии заданы таблично. Требуется так распределить вложения между предприятиями, чтобы общий прирост продукции (в млн. р.) был максимальным.
млн. р. Функции прироста продукции от вложенных средств на каждом предприятии заданы таблично. Требуется так распределить вложения между предприятиями, чтобы общий прирост продукции (в млн. р.) был максимальным.
| Денежные средства, Х | Доход от вложения средств в предприятие | |||
| I | II | III | IV | |
| 0 | 10 | 15 | 13 | 14 |
| 80 | 13 | 20 | 17 | 16 |
| 160 | 16 | 22 | 21 | 23 |
| 240 | 21 | 25 | 26 | 25 |
| 320 | 25 | 30 | 28 | 27 |
| 400 | 25 | 32 | 30 | 32 |
Домашнее задание:
Распределить средства инвестора между четырьмя предприятиями таким образом, чтобы доход от их вложения был бы максимальным. Данные по предприятиям указаны в таблице.
| Денежные средства, Х | Доход от вложения средств в предприятие | |||
| I | II | III | IV | |
| 15 | 3,5 | 3,8 | 3,9 | 4,2 |
| 30 | 3,6 | 3,9 | 4,2 | 4,5 |
| 45 | 4,0 | 4,2 | 4,4 | 5,0 |
| 60 | 4,3 | 4,4 | 5,0 | 5,2 |
| 75 | 4,5 | 4,9 | 5,3 | 5,5 |
Практическое занятие 11
1. Дана платежная матрица. Определите оптимальные стратегии игроков, верхнюю и нижнюю цену игры.
 I II I II
| В1 | В2 | В3 | В4 | В5 | В6 |
| А1 | 20 | 40 | 50 | 70 | 10 | 30 |
| А2 | 15 | 25 | 70 | 50 | 20 | 10 |
| А3 | 80 | 35 | 40 | 80 | 90 | 25 |
| А4 | 45 | 70 | 90 | 70 | 25 | 55 |
2. Определите оптимальную стратегию в «игре с природой», заданной следующей платежной матрицей:
 I II I II
| П1 | рi1 | П2 | рi2 | П3 | рi3 | П4 | рi4 |
| А1 | 20 | 0,15 | 40 | 0,25 | 50 | 0,3 | 70 | 0,25 |
| А2 | 15 | 0,35 | 25 | 0,15 | 70 | 0,25 | 50 | 0,25 |
| А3 | 80 | 0,3 | 35 | 0,4 | 40 | 0,35 | 80 | 0,4 |
| А4 | 45 | 0,2 | 70 | 0,2 | 90 | 0,1 | 70 | 0,1 |
Составьте матрицу рисков и определите оптимальную стратегию по критерию минимального риска.
3. Определите оптимальную стратегию в «игре с природой», заданной платежной матрицей. Составьте матрицу рисков и определите оптимальную стратегию по критерию минимального риска.
 I II I II
| П1 | рi1 | П2 | рi2 | П3 | рi3 | П4 | рi4 |
| А1 | 10 | 0,1 | 15 | 0,15 | 25 | 0,25 | 20 | 0,2 |
| А2 | 20 | 0,15 | 25 | 0,1 | 35 | 0,1 | 10 | 0,3 |
| А3 | 15 | 0,25 | 10 | 0,2 | 20 | 0,15 | 30 | 0,1 |
| А4 | 25 | 0,2 | 40 | 0,3 | 30 | 0,1 | 40 | 0,1 |
| А5 | 40 | 0,2 | 35 | 0,15 | 55 | 0,15 | 60 | 0,1 |
| А6 | 30 | 0,1 | 20 | 0,1 | 10 | 0,25 | 50 | 0,2 |
4. Определите оптимальную стратегию в «игре с природой», заданной платежной матрицей. Составьте матрицу рисков и определите оптимальную стратегию по критерию минимального риска.
 I II I II
| П1 | рi1 | П2 | рi2 | П3 | рi3 | П4 | рi4 | П5 | рi5 |
| А1 | 25 | 0,2 | 55 | 0,2 | 35 | 0,35 | 60 | 0,25 | 25 | 0,35 |
| А2 | 35 | 0,25 | 60 | 0,1 | 25 | 0,15 | 50 | 0,25 | 35 | 0,15 |
| А3 | 20 | 0,1 | 45 | 0,35 | 20 | 0,15 | 40 | 0,2 | 45 | 0,1 |
| А4 | 40 | 0,35 | 70 | 0,15 | 40 | 0,15 | 50 | 0,2 | 65 | 0,25 |
| А5 | 45 | 0,1 | 30 | 0,2 | 30 | 0,2 | 30 | 0,1 | 25 | 0,15 |
5. Перед администрацией муниципального образования стоит задача по ремонту дорог в трех микрорайонах города. На выполнение работ претендуют 4 компании. По предыдущим результатам сотрудничества имеются следующие данные: первая компания может превысить запланированную стоимость работ на 15 % в каждом микрорайоне с вероятностью 10 %, 11 %, 9 % соответственно; вторая компания может превысить запланированную стоимость работ на 14 % в каждом микрорайоне с вероятностью 15 %, 10 %, 12 % соответственно; третья компания может превысить запланированную стоимость работ на 16 % в каждом микрорайоне с вероятностью 9 %, 8 %, 10 % соответственно; четвертая компания может превысить запланированную стоимость работ на 13 % в каждом микрорайоне с вероятностью 11 %, 12 %, 14 % соответственно. Выбрать наиболее надежную фирму для выполнения ремонтных работ в рамках заложенной в бюджет стоимости, если для ремонта дорог в первом микрорайоне запланировано 3 млн. руб., второго – 3,5 млн. руб., третьего – 2,8 млн. руб.
6. Перед администрацией муниципального образования стоит задача строительства школ в пяти микрорайонах города. На выполнение работ претендуют 3 компании. По предыдущим результатам сотрудничества имеются следующие данные: первая компания может превысить запланированную стоимость работ на 20 % в каждом микрорайоне с вероятностью 12 %, 13 %, 10 % соответственно; вторая компания может превысить запланированную стоимость работ на 18 % в каждом микрорайоне с вероятностью 14 %, 15 %, 13 % соответственно; третья компания может превысить запланированную стоимость работ на 16 % в каждом микрорайоне с вероятностью 21 %, 19 %, 22 % соответственно. Выбрать наиболее надежную фирму для строительства школ в рамках заложенной в бюджет стоимости, если для строительства школ в первом микрорайоне запланировано 230 млн. руб., второго – 350 млн. руб., третьего – 310 млн. руб.
Домашнее задание:
1. Определите минимаксные стратегии игроков (нижнюю и верхнюю цены игры).
 I II I II
| В1 | В2 | В3 | В4 | В5 |
| А1 | 5 | 8 | 7 | 6 | 3 |
| А2 | 10 | 12 | 4 | 7 | 2 |
| А3 | 15 | 10 | 8 | 7 | 4 |
| А4 | 10 | 7 | 8 | 12 | 6 |
| А5 | 7 | 10 | 11 | 3 | 5 |
| А6 | 7 | 2 | 3 | 12 | 4 |
2. Определите оптимальную стратегию в «игре с природой», заданной платежной матрицей. Составьте матрицу рисков и определите оптимальную стратегию по критерию минимального риска.
 I II I II
| П1 | рi1 | П2 | рi2 | П3 | рi3 | П4 | рi4 |
| А1 | 25 | 0,1 | 15 | 0,15 | 15 | 0,25 | 45 | 0,2 |
| А2 | 35 | 0,15 | 20 | 0,1 | 25 | 0,1 | 55 | 0,3 |
| А3 | 60 | 0,25 | 25 | 0,2 | 35 | 0,15 | 25 | 0,1 |
| А4 | 45 | 0,2 | 35 | 0,3 | 15 | 0,1 | 35 | 0,1 |
| А5 | 70 | 0,2 | 45 | 0,15 | 45 | 0,15 | 65 | 0,1 |
| А6 | 50 | 0,1 | 20 | 0,1 | 65 | 0,25 | 70 | 0,2 |
3. Сформулировать и решить задачу для нахождения минимаксных стратегий, нижней и верхней цен игры.
4. Сформулировать и решить задачу игры с «природой».
Библиографический список
1. Багриновский К.А., Бусыгин В.П. Математика плановых решений. - М.: Наука, 1980.
2. Бизнес-процесс реинжиниринг и проектирование информационных систем. Материалы семинара. - М.:МГУЭСИ - РосНИИ ИТСАП, 1996. - 100 с.
3. Болтянский В.Г. Математические методы оптимального управления. – М.: Наука, 1969.
4. Гнеденко Б.В. Математика и контроль качества продукции.- М.: Знание, 1978. – 64 с.
5. Гольштейн Е.Г. Выпуклое программирование (элементы теории). – М.: Наука, 1970.
6. Жданова Г.А. Эффект лояльности как базисный элемент работы с покупателями. - Предприятия России в транзитивной экономике. Материалы международной научно-практической конференции. Часть I. - Ярославль: Концерн «Подати», 2002.
7. Математическая экономика на персональном компьютере. Пер. с яп./ М. Кубонива, М. Табата, С.Табата, Ю. Хасэбэ; Под ред. М. Кубонива. - М.: Финансы и статистика, 1991. - 304 с.
8. Моисеев Н.Н. Математические задачи системного анализа. - М.: Наука, 1981. - 488 с.
9. Нейлор Т. Машинные имитационные эксперименты с моделями экономических систем. - М.: Мир, 1975. - 500 с.
10. Нейман Дж.фон, Моргенштейн О. Теория игр и экономическое поведение. - М.: Наука, 1970.
11. Неуймин Я.Г. Модели в науке и технике. История, теория, практика. - Л.: Наука, 1984. - 190 с.
12. Орлов А.И. Математические модели отдельных сторон обучения математике. – В: «Сб. научно-методических статей по математике. (Проблемы преподавания математики в вузах.)» Вып.7. - М.: Высшая школа, 1978. С.28-34.
13. Орлов А.И. Менеджмент Учебник. М.: Издательство "Изумруд", 2003
14. Орлов А.И. Теория принятия решений. – М.: Экзамен, 2003 (в печати).
15. Орлов А.И. Устойчивость в социально-экономических моделях. - М.: Наука, 1979. -296 с.
16. Орлов А.И. Эконометрика. – М.: Экзамен, 2003. – 576 с.
17. Основы математического моделирования социально-экономических процессов : учебник и практикум для бакалавриата и магистратуры / И. Н. Дубина. — М. : Издательство Юрайт, 2018. — 349 с..
18. Пойа Д. Математическое открытие. – М.: Наука, 1970.
19. Фомин Г. П. Математические методы и модели в коммерческой деятельности: Учебник. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2005. — 616 с
Приложение А
Оформление титульного листа контрольной работы
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«РОССИЙСКАЯ АКАДЕМИЯ НАРОДНОГО ХОЗЯЙСТВА И
ГОСУДАРСТВЕННОЙ СЛУЖБЫ
ЛАБОРАТОРНАЯ РАБОТА
по дисциплине_____________________________________________
тема______________________________________________________
Выполнил(а):
студент(ка)___курса
___________формы обучения
группы____________________
Ф.И.О.____________________
__________________________
подпись___________________
Проверил:
Должность, звание__________
Ф.И.О.____________________
__________________________
Оценка____________________
Подпись___________________
Калининград, 20__г.
Основы математического моделирования социально-экономических процессов
Калининград
2018
УДК 330.101
ББК 65
Б21
Рецензенты:
канд. экон. наук, доцент Есенжулова Л. С., доцент кафедры экономики и менеджмента Западного филиала РАНХиГС
канд. физико-матем. наук, доцент Милованов В. Ф., доцент БФУ им. И. Канта
Б21 Балясникова Е. В., Скопич Д. Л.
Основы моделирования социально-экономических процессов /Е. В. Балясникова, Д. Л. Скопич. –Саратов: Амирит. 2018. – с.
Учебное пособие предназначено для студентов, обучающихся по направлениям 38.03.04 «Государственное и муниципальное управление», 38.03.02 «Менеджмент». Учебное пособие содержит основные материалы по дисциплине «Основы моделирования социально-экономических процессов». В нем представлены основные вопросы лекционного курса по дисциплине и для подготовки к практическим занятиям, задания для практического выполнения студентами, задания для выполнения на лабораторных занятиях с методическими рекомендациями по их выполнению.
Допущено (рекомендовано) Ученым советом Западного филиала РАНХиГС в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлениям 38.03.04 «Государственное и муниципальное управление», 38.03.02 «Менеджмент»
Учебное пособие рекомендовано к изданию Ученым советом филиала «__» ____________ 201_г., протокол №____.
.
© Балясникова Е. В., Скопич Д. Л.
©Западный филиал РАНХиГС, 2018
Оглавление
Раздел 1. Основные понятия математического моделирования социально-экономических процессов 4
Тема 1. Основные понятия и технология построения математических моделей социально-экономических процессов. 4
Практическое занятие 1. 17
Тема 2. Задачи управления социально-экономическими процессами как объект математического моделирования и прогнозирования. 18
Практическое занятие 2. 21
Раздел 2. Математические модели социально-экономических процессов принятия решений. Методы оптимизации. 22
Тема 3. Модели линейного программирования. 22
Практическое занятие 3. 26
Графический метод решения задач линейного программирования. 28
Практическое занятие 4. 33
Симплексный метод решения задач линейного программирования. 35
Практическое занятие 5. 42
Двойственный симплексный метод. 44
Практическое занятие 6. 49
Постановка и правила построения двойственной задачи. 50
Практическое занятие 7. 53
Транспортная задача. 54
Практическое занятие 8. 65
Решение задач линейного программирования инструментами MS Excel 66
Лабораторная работа по теме «Модели линейного программирования» 70
Тема 4. Специальные задачи линейного программирования. 97
Практическое занятие 9. 97
Тема 5. Динамическое программирование. 100
Практическое занятие 10. 107
Тема 6. Теоретико-игровые модели принятия решений. 108
Практическое занятие 11. 137
Тема 7. Прогнозирование с помощью парной и множественной регрессии. 140
Тема 8: Моделирование временных рядов. 152
Библиографический список. 160
Приложение А.. 162
Оформление титульного листа контрольной работы.. 162
Раздел 1. Основные понятия математического моделирования социально-экономических процессов
Тема 1. Основные понятия и технология построения математических моделей социально-экономических процессов
Рассмотрим ряд основных понятий, связанных с системным анализом и моделированием социально-экономических систем, чтобы с их помощью более полно раскрыть суть такого ключевого понятия, как экономико-математические методы. Термин "экономико-математические методы" понимается в свою очередь как обобщающее название комплекса экономических и математических научных дисциплин, объединенных для изучения социально-экономических систем и процессов.
Под социально-экономической системой понимают сложную вероятностную динамическую систему, охватывающую процессы производства, обмена, распределения и потребления материальных и других благ. Она относится к классу кибернетических систем, т. е. систем управляемых.
Центральным понятием кибернетики является понятие «система». Системой называется комплекс взаимосвязанных элементов вместе с отношениями между элементами и между их атрибутами. Исследуемое множество элементов можно рассматривать как систему, если выявлены четыре признака:
- целостность системы, т. е. принципиальная несводимость свойств системы к сумме свойств составляющих ее элементов;
- наличие цели и критерия исследования данного множества элементов,
- наличие более крупной, внешней по отношению к данной, системы, называемой «средой»;
- возможность выделения в данной системе взаимосвязанных частей (подсистем).
Основным методом исследования систем является метод моделирования, т. е. способ теоретического анализа и практического действия, направленный на разработку и использование моделей. При этом под моделью будем понимать образ реального объекта (процесса) в материальной или идеальной форме (т. е. описанный знаковыми средствами на каком-либо языке), отражающий существенные свойства моделируемого объекта (процесса) и замещающий его в ходе исследования и управления. Метод моделирования основывается на принципе аналогии, т. е. возможности изучения реального объекта не непосредственно, а через рассмотрение подобного ему и более доступного объекта, его модели. В дальнейшем мы будем говорить только об экономико-математическом моделировании, т. е. об описании знаковыми математическими средствами социально-экономических систем.
Моде́ль (фр. modèle, от лат. modulus — «мера, аналог, образец») — это система, исследование которой служит средством для получения информации о другой системе; представление некоторого реального процесса, устройства или концепции.
Модель есть абстрактное представление реальности в какой-либо форме (например, в математической, физической, символической, графической или дескриптивной), предназначенное для представления определенных аспектов этой реальности и позволяющее получить ответы на изучаемые вопросы
Моделирование это построение моделей, предназначенных для изучения и исследования объектов, процессов или явлений.
Поведение модели должно, так или иначе, отражать особенности поведения оригинала. Смысл моделирования заключается в том, что модель системы проще оригинала и ее исследование провести легче и дешевле. Изменение параметров модели позволит изучить их влияние на оригинал.
Основные цели моделирования в разных ситуациях:
1. Понимание и объяснение причин и факторов, влияющих на определенное поведение оригинала.
2. Прогноз поведения оригинала.
3. Разработка и проектирование технических систем или экономических планов.
4. Автоматизация управления техническими системами и устройствами.
5. Улучшение (оптимизация) характеристик той или иной искусственной системы (технической или экономической). Модели, которые строятся с этой целью, называются оптимизационными.
6. Обучение (студентов, персонала и т.п.).
С точки зрения характера получаемой модели различают следующие основные виды моделирования:
1. Вербальное моделирование производится на основе обычного человеческого языка. Вербальная модель – это просто словесное описание оригинала.
2. Графическое моделирование – это представление модели в виде некоего изображения. Например, географическая карта является графической моделью земной поверхности; чертеж детали является ее графической моделью; структурная схема административного устройства организации (учреждения, фирмы и др.) является графической моделью этой организации, на основе которой можно, например, изучать и совершенствовать процедуры документооборота или принятия решений. Вербальные и графические модели широко используются при обучении.
3. Натурное моделирование, при котором оригинал заменяется своим физическим подобием (макетом). Такие модели также используются в обучении (примером могут служить наглядные пособия в учебных лабораториях; натурными моделями являются также всевозможные тренажеры для обучения шоферов, пилотов, операторов сложных производственных систем и др.). Макетами пользуются и при разработке некоторых технических систем (например, при разработке новых самолетов или автомобилей их макеты сначала обдувают воздухом в аэродинамических трубах для выбора обтекаемой формы корпуса).
4. Математическое моделирование основано на использовании математического аппарата. Существует большое количество разновидностей математических моделей, которые в последнее время объединяют общим наименованием – информационные модели. По характеру зависимости от времени математические модели делятся на статические модели, характеристики которых не изменяются во времени и динамические – с переменными во времени характеристиками.
Экономические процессы всегда развиваются во времени. Статической экономическая модель получается, если все ее характеристики отнести к одному и тому же моменту времени. Динамические модели в экономике, в свою очередь, делятся на дискретные и непрерывные. В дискретных моделях изменение параметров связано только с отдельными моментами времени. В непрерывных моделях параметры изменяются во времени плавно.
Математическое описание системы-оригинала может быть получено разными способами.
При теоретическом моделировании система описывается набором уравнений, которые получаются на базе основных законов природы (при моделировании природных и технических систем), а также здравого смысла, человеческого опыта или более или менее обоснованных логически предположений (гипотез) о процессах, происходящих в системе. Именно такие умозрительные предположения часто используются при теоретическом моделировании экономических и социальных систем.
При эмпирическом моделировании формулы и функции, описывающие те или иные стороны поведения системы, получаются путем прямого измерения характеристик системы и обработки полученных экспериментальных данных. В экономических и социальных системах аналогами экспериментальных исследований являются различные статистические обследования.
Важнейшими свойствами моделей являются их полнота, адекватность и точность. Полнота характеризуется тем, какое количество характеристик оригинала отображает модель. Любая модель неполна по сравнению с оригиналом и какие-то характеристики при моделировании "теряются". Однако эти потерянные характеристики могут быть несущественными с точки зрения целей моделирования, а попытка их учесть путем дополнения модели только усложнит ее и затруднит исследование. Уровень полноты модели влияет на ее адекватность. Адекватность – это соответствие, совпадение каких-либо параметров, удовлетворительное с точки зрения определенных целей, т.е. способна дать ответ на поставленные разработчиком вопросы. Точность характеризуется разностью между фактическими и расчетными значениями исследуемого показателя.
Социально-экономические системы относятся, как правило, к так называемым сложным системам. Сложные системы в экономике обладают рядом свойств, которые необходимо учитывать при их моделировании, иначе невозможно говорить об адекватности построенной экономической модели.
Важнейшие свойства сложных систем:
1. Эмерджентность как проявление в наиболее яркой форме свойства целостности системы, т. е. наличие у экономической системы таких свойств, которые не присущи ни одному из составляющих систему элементов, взятому в отдельности, вне системы. Эмерджентность есть результат возникновения между элементами системы так называемых синергических связей, которые обеспечивают увеличение общего эффекта до величины, большей, чем сумма эффектов элементов системы, действующих независимо. Поэтому социально-экономические системы необходимо исследовать и моделировать в целом.
2. Массовый характер экономических явлений и процессов. Закономерности экономических процессов не обнаруживаются на основании небольшого числа наблюдений. Поэтому моделирование в экономике должно опираться на массовые наблюдения.
3. Динамичность экономических процессов, заключающаяся в изменении параметров и структуры экономических систем под влиянием среды (внешних факторов).
4. Случайность и неопределенность в развитии экономических явлений. Поэтому экономические явления и процессы носят в основном вероятностный характер, и для их изучения необходимо применение экономико-математических моделей на базе теории вероятностей и математической статистики.
5. Открытость систем, участвующих в экономической системе. Их невозможно изолировать от окружающей среды, чтобы наблюдать и исследовать их в чистом виде.
6. Активная реакция на появляющиеся новые факторы, последствия которой не всегда предсказуемы.
Выделенные свойства социально-экономических систем осложняют процесс их моделирования, однако эти свойства следует постоянно иметь в виду при рассмотрении различных аспектов экономико-математического моделирования, начиная с выбора типа модели и заканчивая вопросами практического использования результатов моделирования.
Процесс моделирования, в том числе и экономико-математического, включает в себя три структурных элемента:
- объект исследования;
- субъект (исследователь);
- модель, опосредующую отношения между познающим субъектом и познаваемым объектом.
Этапы моделирования:
1 этап: необходимо изучить оригинал: его свойства, систему и подсистемы, входящие в нее, взаимодействие с внешней средой и т. д., из которых отобрать определяющие (основные) составляющие и свойства объекта, определить возможность качественной и количественной их оценки. Выбрать метод моделирования и на основе отобранных переменных построить модель. Познавательные возможности модели определяются тем, что модель отображает лишь некоторые существенные черты исходного объекта, поэтому любая модель замещает оригинал в строго ограниченном смысле. Из этого следует, что для одного объекта может быть построено несколько моделей, отражающих определенные стороны исследуемого объекта или характеризующих его с разной степенью детализации.
2 этап процесса моделирования модель выступает как самостоятельный объект исследования. Одну из форм такого исследования составляет проведение модельных экспериментов, при которых целенаправленно изменяются условия функционирования модели и систематизируются данные о ее «поведении». Конечным результатом этого этапа является совокупность знаний о модели в отношении существенных сторон объекта-оригинала, которые отражены в данной модели.
3 этап заключается в переносе знаний с модели на оригинал, в результате чего формируется множество знаний об исходном объекте и осуществляется переход с языка модели на язык оригинала. С достаточным основанием переносить какой-либо результат с модели на оригинал можно лишь в том случае, если этот результат соответствует признакам сходства оригинала и модели (признакам адекватности).
4 этап: осуществляются практическая проверка полученных с помощью модели знаний и их использование для построения обобщающей теории реального объекта и для его целенаправленного преобразования или управления им. В итоге происходит возврат к проблематике объекта-оригинала.
Моделирование представляет собой циклический процесс: за первым четырехэтапным циклом может последовать второй, третий и т. д. При этом знания об исследуемом объекте расширяются и уточняются, а первоначально построенная модель постепенно совершенствуется. Таким образом, в методологии моделирования заложены большие возможности самосовершенствования.
Перейдем теперь непосредственно к процессу экономико-математического моделирования, т. е. описания экономических и социальных систем и процессов в виде экономико-математических моделей. Эта разновидность моделирования обладает рядом существенных особенностей, связанных как с объектом моделирования, так и с применяемыми аппаратом и средствами моделирования. Поэтому целесообразно более детально проанализировать последовательность и содержание этапов экономико-математического моделирования, выделив следующие шесть этапов:
1. Постановка экономической проблемы и ее качественный анализ. На этом этапе требуется сформулировать сущность проблемы, принимаемые предпосылки и допущения. Необходимо выделить важнейшие черты и свойства моделируемого объекта, изучить его структуру и взаимосвязь его элементов, хотя бы предварительно сформулировать гипотезы, объясняющие поведение и развитие объекта.
2. Построение математической модели. Это этап формализации экономической проблемы, т. е. выражения ее в виде конкретных математических зависимостей (функций, уравнений, неравенств и др.). Построение модели подразделяется в свою очередь на несколько стадий. Сначала определяется тип экономико-математической модели, изучаются возможности ее применения в данной задаче, уточняются конкретный перечень переменных и параметров и форма связей. Для некоторых сложных объектов целесообразно строить несколько разноаспектных моделей; при этом каждая модель выделяет лишь некоторые стороны объекта, а другие стороны учитываются агрегировано и приближенно. Оправдано стремление построить модель, относящуюся к хорошо изученному классу математических задач, что может потребовать некоторого упрощения исходных предпосылок модели, не искажающего основных черт моделируемого объекта. Однако возможна и такая ситуация, когда формализация проблемы приводит к неизвестной ранее математической структуре.
3. Математический анализ модели. На этом этапе чисто математическими приемами исследования выявляются общие свойства модели и ее решений. В частности, важным моментом является доказательство существования решения сформулированной задачи. При аналитическом исследовании выясняется, единственно ли решение, какие переменные могут входить в решение, в каких пределах они изменяются, каковы тенденции их изменения и т. д. Однако модели сложных экономических объектов с большим трудом поддаются аналитическому исследованию; в таких случаях переходят к численным методам исследования.
4. Подготовка исходной информации. В экономических задачах это, как правило, наиболее трудоемкий этап моделирования, так как дело не сводится к пассивному сбору данных. Математическое моделирование предъявляет жесткие требования к системе информации; при этом надо принимать во внимание не только принципиальную возможность подготовки информации требуемого качества, но и затраты на подготовку информационных массивов. В процессе подготовки информации используются методы теории вероятностей, теоретической и математической статистики для организации выборочных обследований, оценки достоверности данных и т.д. При системном экономико-математическом моделировании результаты функционирования одних моделей служат исходной информацией для других.
5. Численное решение. Этот этап включает разработку алгоритмов численного решения задачи, выбор программного обеспечения и непосредственное проведение расчетов, при этом значительные трудности вызываются большой размерностью экономических задач. Обычно расчеты на основе экономико-математической модели носят многовариантный характер. Численное решение существенно дополняет результаты аналитического исследования, а для многих моделей является единственно возможным.
6. Анализ численных результатов и их применение. На этом этапе, прежде всего, решается важнейший вопрос о правильности и полноте результатов моделирования и применимости их как в практической деятельности, так и в целях усовершенствования модели. Поэтому в первую очередь должна быть проведена проверка адекватности модели по тем свойствам, которые выбраны в качестве существенных (другими словами, должны быть произведены верификация и валидация модели). Применение численных результатов моделирования в экономике направлено на решение практических задач (анализ экономических объектов, экономическое прогнозирование развития хозяйственных и социальных процессов, выработка управленческих решений на всех уровнях хозяйственной иерархии).
Перечисленные этапы экономико-математического моделирования находятся в тесной взаимосвязи, в частности, могут иметь место возвратные связи этапов. Так, на этапе построения модели может выясниться, что постановка задачи или противоречива, или приводит к слишком сложной математической модели; в этом случае исходная постановка задачи должна быть скорректирована. Наиболее часто необходимость возврата к предшествующим этапам моделирования возникает на этапе подготовки исходной информации. Если необходимая информация отсутствует или затраты на ее подготовку слишком велики, приходится возвращаться к этапам постановки задачи и ее формализации, чтобы приспособиться к доступной исследователю информации.
Дата: 2019-05-28, просмотров: 507.
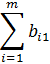
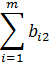
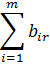
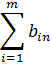
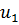
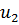
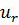
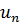
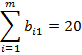
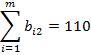
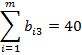
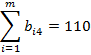
 2
2