Графический метод решения задач линейного программирования – это наиболее простой и наглядный способ. Применение графического метода для решения задач линейного программирования возможно только в случае двух переменных, так как невозможно будет изобразить график решения на плоскости.
Алгоритм графического метода
1) На плоскости 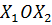 строим прямые, уравнения которых получаются путем замены знаков неравенств на знаки равенств в ограничениях.
строим прямые, уравнения которых получаются путем замены знаков неравенств на знаки равенств в ограничениях.
2) Определяем полуплоскости, заданные неравенствами ограничений. Для этого в каждое неравенство подставляем координаты любой точки (наиболее удобно подставлять координаты точки (0,0)). Если полученное неравенство верное, то выбранная точка принадлежит искомой полуплоскости, тогда штриховку от ограничивающей прямой направляем в сторону выбранной точки. Если полученное неравенство неверное, то выбранная точка не принадлежит искомой полуплоскости, и штриховку от ограничивающей прямой направляем в противоположную выбранной точке сторону.
3) Определяем многоугольник решений (область допустимых решений) – область, в которой любая точка является решением системы ограничений задачи. Многоугольник решений получается пересечением всех полуплоскостей, определяемых системой ограничений. Многоугольник решений может быть замкнутым, неограниченной многоугольной областью, лучом, отрезком, точкой или пустой областью (нет области, где пересеклись все полуплоскости). В последнем случае говорят, что ограничения несовместны, и задача не будет иметь решения.
4)Строим вектор 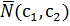 (градиент), указывающий направление возрастания целевой функции.
(градиент), указывающий направление возрастания целевой функции. 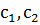 - это коэффициенты целевой функции.
- это коэффициенты целевой функции.
5) Строим начальную прямую целевой функции 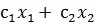 =0. Эта прямая перпендикулярна вектору
=0. Эта прямая перпендикулярна вектору 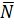 .
.
6) Для нахождения максимума передвигаем прямую 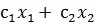 =0 в сторону вектора
=0 в сторону вектора 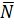 до крайнего касания прямой с многоугольником решения – это точка максимума. Определяем прямые, пересечением которых образуется найденная точка. Находим координаты точки путем решения системы уравнений прямых. Находим максимум функции, подставив координаты точки в функцию.
до крайнего касания прямой с многоугольником решения – это точка максимума. Определяем прямые, пересечением которых образуется найденная точка. Находим координаты точки путем решения системы уравнений прямых. Находим максимум функции, подставив координаты точки в функцию.
Для нахождения минимума передвигаем прямую 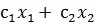 =0 в противоположную вектору
=0 в противоположную вектору 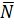 сторону до крайнего касания прямой с многоугольником решения (или до первого касания с многоугольником решений при движении в направлении вектора
сторону до крайнего касания прямой с многоугольником решения (или до первого касания с многоугольником решений при движении в направлении вектора 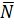 ) – это точка минимума. Определяем прямые, пересечением которых образуется найденная точка. Находим координаты точки путем решения системы уравнений прямых. Находим минимум функции, подставив координаты точки в функцию.
) – это точка минимума. Определяем прямые, пересечением которых образуется найденная точка. Находим координаты точки путем решения системы уравнений прямых. Находим минимум функции, подставив координаты точки в функцию.
Пример 2. Решить графическим методом задачу.
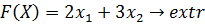
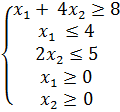
1) На плоскости 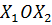 строим прямые. Так как ограничений в условии задачи 5, то и прямых тоже 5.
строим прямые. Так как ограничений в условии задачи 5, то и прямых тоже 5.
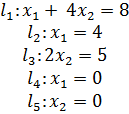
Прямые 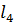 и
и 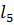 - это оси координат, соответственно
- это оси координат, соответственно  и
и  .
.
2) Определим полуплоскости, заданные неравенствами ограничений. Для этого в каждое неравенство подставляем координаты точки (0, 0).
Подставив (0, 0) в первое неравенство, получили 0+4×0≥0 – неверное неравенство, следовательно, точка (0, 0) не принадлежит искомой полуплоскости, и штриховка будет от прямой 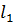 в сторону полуплоскости, которая не содержит точку (0, 0).
в сторону полуплоскости, которая не содержит точку (0, 0).
Подставив (0, 0) во второе неравенство, получили 0≤0 – верное неравенство, следовательно, точка (0, 0) принадлежит искомой полуплоскости, и штриховка будет от прямой 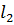 в сторону полуплоскости, которая содержит точку (0, 0).
в сторону полуплоскости, которая содержит точку (0, 0).
Подставив (0, 0) в третье неравенство, получили 0≤0 – верное неравенство, следовательно, точка (0, 0) принадлежит искомой полуплоскости, и штриховка будет от прямой 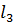 в сторону полуплоскости, которая содержит точку (0, 0).
в сторону полуплоскости, которая содержит точку (0, 0).
Неравенства 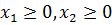 ограничивают область допустимых решений в I четверти, то есть все значения
ограничивают область допустимых решений в I четверти, то есть все значения  и
и  должны быть неотрицательными.
должны быть неотрицательными.

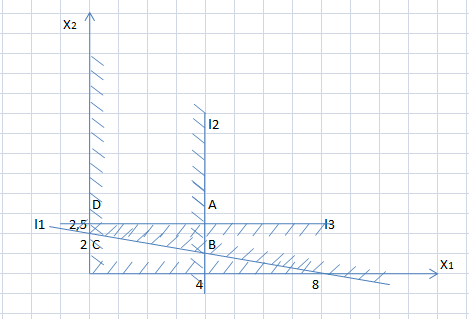
Рис. 1.1. Многоугольник решений
3) Многоугольник ABCD – это область, где пересеклись все полуплоскости, следовательно он является многоугольником решений (рис. 1.1).
4) Построим вектор 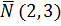 (рис. 1.2).
(рис. 1.2).
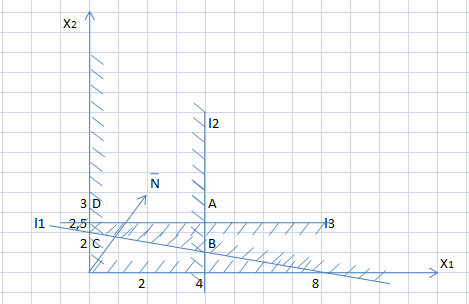
Рис. 1.2. Градиент
5) Построим начальную 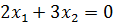 (рис. 1.3). Это прямая
(рис. 1.3). Это прямая 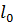 , проходящая через точку (0, 0), перпендикулярно вектору
, проходящая через точку (0, 0), перпендикулярно вектору 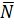 .
.
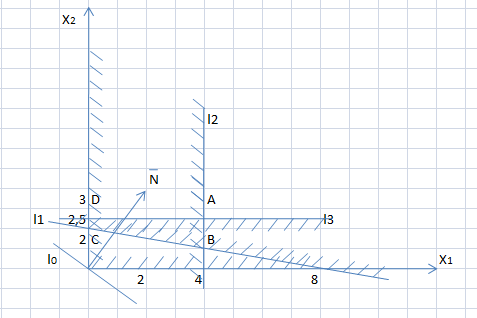
Рис. 1.3. Прямая 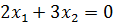
6) Так как в задаче указано, что целевая функция стремится к extr, то это значит, что необходимо найти максимум и минимум функции. Найдем точку максимума. Для этого передвигаем прямую 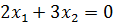 в направлении, указанном вектором
в направлении, указанном вектором 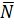 до крайнего касания прямой с многоугольником решения – это точка А (рис. 1.4).
до крайнего касания прямой с многоугольником решения – это точка А (рис. 1.4).
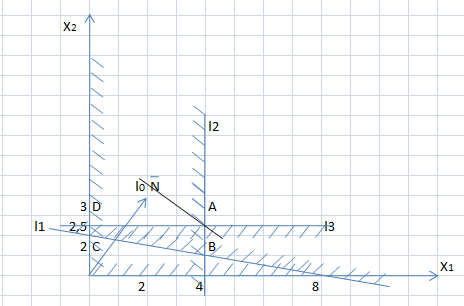
Рис. 1.4. Точка максимума
Точка максимума образуется пересечением прямых 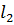 и
и 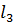 , то есть
, то есть 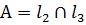 . Для того, чтобы найти координаты точки А необходимо решить систему уравнений, образованную из уравнений прямых
. Для того, чтобы найти координаты точки А необходимо решить систему уравнений, образованную из уравнений прямых 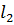 и
и 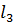 :
:
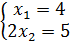 .
.
Из системы уравнений получаем, что координаты точки А (4; 2,5). Чтобы найти максимальное значение функции, подставим координаты точки А в функцию и получим 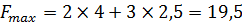 .
.
Чтобы найти точку минимума, нужно передвигать прямую 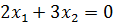 в направлении вектора
в направлении вектора 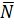 до первого касания прямой с многоугольником решения – это точка С (рис. 1.5).
до первого касания прямой с многоугольником решения – это точка С (рис. 1.5).
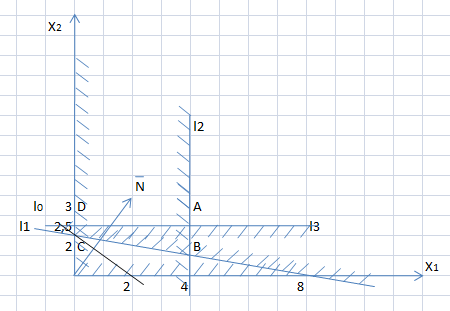
Рис. 1.5. Точка минимума
Точка минимума образуется пересечением прямых 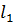 и
и 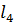 , то есть
, то есть 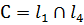 . Для того, чтобы найти координаты точки С необходимо решить систему уравнений, образованную из уравнений прямых
. Для того, чтобы найти координаты точки С необходимо решить систему уравнений, образованную из уравнений прямых 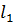 и
и 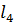 :
:
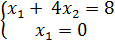 .
.
Из системы уравнений получаем, что координаты точки С (0; 2). Чтобы найти минимальное значение функции, подставим координаты точки С в функцию и получим 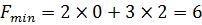 .
.
Ответ: Максимальное значение функции равно 19,5 при 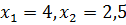 , минимальное значение функции равно 6 при
, минимальное значение функции равно 6 при 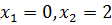 .
.
Реальные задачи социально-экономических процессов чаще всего содержат больше двух переменных, поэтому применить графический метод для их решения невозможно.
Практическое занятие 4
Выучить алгоритм графического метода.
Решить задачи:
1. Постройте на плоскости X1OX2 область решений системы линейных неравенств и найдите максимальное и минимальное значения линейной функции в этой области:
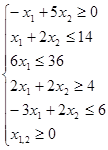 ,
, 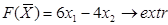
2. Найдите вариант приготовления морса клубничного и морса брусничного, который обеспечивает максимальный доход от продажи, если имеется 5 т смеси 1-го вида и 30 т смеси 2-го вида. На изготовление клубничного идет 60% смеси 1-го вида и 40% смеси 2-го вида, на изготовление морса брусничного идет 80% смеси 1-го вида и 20% смеси 2-го вида. Реализуется 1 л морса клубничного за 50 руб., а 1 л морса брусничного за 60 руб. Задачу решите графическим методом.
3. Фирма производит два сорта хлеба Пшеничный 1 сорта и Пшеничный 2 сорта. Для производства 1 буханки Пшеничного 1 сорта требуется 0,02 ч работы оборудования, а для Пшеничного 2 сорта - 0,04 ч, а теста на них составляет 0,6 кг и 0,5 кг на 1 буханку соответственно. Ежедневно в распоряжении фирмы 160 кг теста и 24 ч работы оборудования. Доход от реализации 1 буханки хлеба Пшеничного 1 сорта составляет 35 руб., а хлеба Пшеничный 2 сорта - 25 руб.
Определите ежедневный план производства хлеба каждого сорта, обеспечивающий максимальный доход от их продажи. Задачу решите графическим методом.
Домашнее задание:
1. Постройте на плоскости X1OX2 область решений системы линейных неравенств и найдите максимальное и минимальное значения линейной функции в этой области:
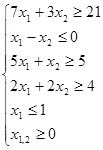 ,
, 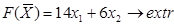
2. Туристическая фирма в летний период обслуживает в среднем 7500 туристов и располагает автобусами двух типов, характеристики которых представлены в таблице:
| Показатели | Автобус | |
| I | II | |
| Пассажировместимость, чел. | 50 | 40 |
| Горючее, т | 120 | 70 |
| Экипаж, чел. | 3 | 2 |
В месяц выделяется 6000 т горючего. Потребность в рабочей силе не превышает 210 человек.
Определите количество автобусов каждого типа, чтобы обеспечить максимальный доход, который составляет от эксплуатации автобуса I типа 2 тыс. руб., II – 1 млн. руб. в месяц. Решите задачу графическим методом.
Дата: 2019-05-28, просмотров: 464.