Каждой задаче линейного программирования можно определенным образом поставить в соответствие другую задачу линейного программирования, называемую двойственной по отношению к данной (исходной) задаче. Исходная и двойственная задачи тесно связаны между собой и образуют пару двойственных задач. Решение одной задачи является решением и другой задачи.
Если при решении задачи не выполняются условия применения симплексного или двойственного симплексного метода, то можно построить двойственную задачу, применить подходящий метод, и это решение будет являться решением исходной задачи.
Правила построения двойственной задачи
1. Если целевая функция прямой задачи стремится к максимуму, то целевая функция двойственной задачи будет стремиться к минимуму, и наоборот.
2. Коэффициенты целевой функции прямой задачи становятся правыми частями ограничений двойственной задачи. Правые части ограничений прямой задачи становятся коэффициентами целевой функции двойственной задачи.
3. Число переменных двойственной задачи равно числу ограничений прямой задачи, а число ограничений двойственной равно числу переменных прямой задачи, и наоборот.
4. Коэффициенты системы ограничений двойственной задачи получаются путем транспонирования матрицы коэффициентов прямой задачи.
5. Каждой переменной прямой задачи соответствует ограничение двойственной задачи. Если на переменную исходной задачи наложено условие неотрицательности, то соответствующее ограничение двойственной задачи будет неравенством, в противном случае равенством. Аналогично связаны между собой ограничения прямой задачи и переменные двойственной.
6. Если ограничение прямой задачи смысла ≥, то в двойственной задаче будет ≤, и наоборот.
Пример 5. Составить задачу, двойственную прямой задаче:
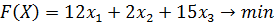
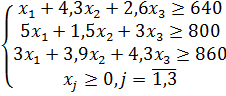
Решение.
Так как неравенств в ограничениях прямой задачи 3, следовательно, переменных в двойственной задаче будет 3. Обозначим их 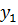 ,
, 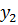 ,
, 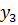 . Целевая функция прямой задачи стремится к минимуму, значит, целевая функция двойственной задачи будет стремиться к максимуму. Коэффициентами целевой функции двойственной задачи станут свободные члены системы неравенств прямой задачи. Целевая функция двойственной задачи имеет вид:
. Целевая функция прямой задачи стремится к минимуму, значит, целевая функция двойственной задачи будет стремиться к максимуму. Коэффициентами целевой функции двойственной задачи станут свободные члены системы неравенств прямой задачи. Целевая функция двойственной задачи имеет вид:
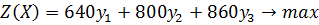
Матрица коэффициентов системы ограниченйи прямой задачи имеет вид:
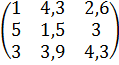
Матрица коэффициентов системы ограничений двойственной получается путем транспонирования матрицы коэффициентов системы ограничений прямой задачи:
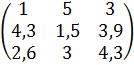
Знаки неравенств ограничений двойственной задачи будут смысла ≤, а свободные члены неравенств – это коэффициенты функции цели прямой задачи. Отсюда система ограничений двойственной задачи будет иметь вид:
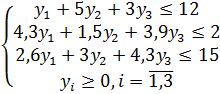
Решив двойственную задачу, мы получим и решение прямой задачи. Соответствие между первоначальными переменными одной из двойственных задач и дополнительными переменными другой задачи:
| Переменные исходной задачи | |
| Первоначальные | Дополнительные |
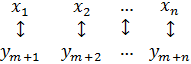
| 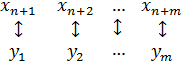
|
| Дополнительные | Первоначальные |
| Переменные двойственной задачи | |
Практическое занятие 7
Выучить правила перехода от прямой задачи к двойственной.
Решить задачи.
1. Записать математическую модель двойственной задачи линейного программирования по заданной прямой задаче:
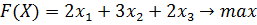 ,
,
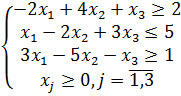
2. Для производства трех изделий А, В и С используются три вида сырья. Каждый из них используется в объеме, не превышающем 180, 210 и 236 кг. Нормы затрат каждого из видов сырья на одно изделие и цена единицы изделий приведены в таблице.
| Вид сырья | Нормы затрат сырья на одно изделие, кг | ||
| А | В | С | |
| 1 | 4 | 2 | 1 |
| 2 | 3 | 1 | 3 |
| 3 | 1 | 2 | 5 |
| Цена изделия, тыс. руб. | 10 | 14 | 12 |
Определить план выпуска изделий, обеспечивающий получение максимального дохода. Составить для данной задачи двойственную и найти оптимальный план двойственной задачи.
Домашнее задание:
Найти решение задачи:
1. 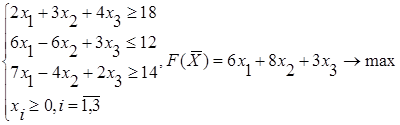
Транспортная задача
Транспортная задача – это задача об оптимальном плане перевозок товаров из пунктов отправления в пункты потребления. Целью транспортной задачи является доставка товаров в определенное время и место при минимальных совокупных затратах трудовых, материальных и финансовых ресурсов или времени доставки.
Выделяют два типа транспортных задач по критерию оптимальности:
- по критерию стоимости – план перевозок является оптимальным, если достигается минимум затрат на его реализацию;
- по критерию времени – план перевозок оптимален, если на него затрачивается минимальное количество времени.
В общем виде задачу можно представить следующим образом: в m пунктах отправления А1, А2, ... , Аm имеется однородный груз в количестве соответственно а1, а2, ... , аm. Этот груз необходимо доставить в n пунктов потребления В1, В2, ... , Вn в количестве соответственно b1, b2, ... , bn. Стоимость перевозки единицы груза (тариф) из пункта Ai в пункт Bj равна сij. Требуется составить такой план перевозок, который позволит вывезти весь товар и имеющий минимальную стоимость (минимальное время перевозки). В зависимости от соотношения между суммарными запасами товара и суммарными потребностями в нем транспортные задачи могут быть закрытыми и открытыми.
Задача называется закрытой, если сумма товара на всех пунктах отправления равна сумме потребностей в товаре на всех пунктах назначения, то есть 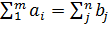 ,
,
Если сумма товара на всех пунктах отправления не равна сумме потребностей в товаре на всех пунктах назначения, то есть 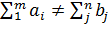 , то задача называется открытой.
, то задача называется открытой.
Обозначим через x ij количество груза, перевозимого из пункта Ai в пункт Bj. Рассмотрим транспортную задачу закрытого типа.
Математическая модель транспортной задачи имеет вид:
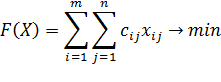
при ограничениях:
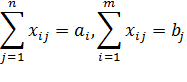
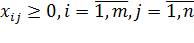 .
.
Оптимальным решением задачи является матрица
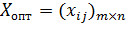 ,
,
удовлетворяющая системе ограничений и обеспечивающая минимальное значение целевой функции.
Алгоритм транспортной задачи
1) Нахождение исходного опорного решения. Данные задачи записываем в таблицу:
|
| bj | b1 | b2 | … | br | … | bn | |||||
| ai |
| |||||||||||
| a1 | x11 | c11 | x12 | c12 | … | x1r | c1r | … | x1n | c1n | ||
| a2 | x21 | c21 | x22 | c22 | … | x2r | c2r | … | x2n | c2n | ||
| … | … | … | … | … | … | … | ||||||
| ak | xk1 | ck1 | xk2 | ck2 | … | xkr | ckr | … | xkn | ckn | ||
| … | … | … | … | … | … | … | ||||||
| am | xm1 | cm1 | xm2 | cm2 | … | xmr | cmr | … | xmn | cmn | ||
Распределение x ij можно проводить с помощью метода минимального элемента. Для этого из всех стоимостей выбираем наименьшую и в эту ячейку записываем меньшее значение из соответствующих значений 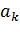 и
и 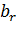 . Если записывается значение пункта отправления, то все оставшиеся ячейки данной строки заполняются знаками ×, если в указанную ячейку заполняется значение пункта потребления, то все оставшиеся ячейки соответствующего столбца заполняются знаками ×. Эти ячейки считаются заполненными. Если ячеек с наименьшей стоимостью несколько, то сначала заполняем ту ячейку, в которую можно записать большее значение.
. Если записывается значение пункта отправления, то все оставшиеся ячейки данной строки заполняются знаками ×, если в указанную ячейку заполняется значение пункта потребления, то все оставшиеся ячейки соответствующего столбца заполняются знаками ×. Эти ячейки считаются заполненными. Если ячеек с наименьшей стоимостью несколько, то сначала заполняем ту ячейку, в которую можно записать большее значение.
Далее из оставшихся незаполненных ячеек снова выбираем наименьшую стоимость и заполняем ячейки аналогично вышеописанному действию. И так заполняем ячейки до тех пор, пока не будут заполнены все ячейки. После того, как все ячейки заполнены необходимо проверить, соответствуют ли значение пунктов отправления суммам по соответствующим строкам, и значения пунктов потребления суммам по соответствующим столбцам.
|
| bj | b1 | b2 | … | br | … | bn |
| ||||
| ai |
| |||||||||||
| a1 | x11 | c11 | x12 | c12 | … | x1r | c1r | … | x1n | c1n | 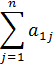
| |
| a2 | x21 | c21 | x22 | c22 | … | x2r | c2r | … | x2n | c2n | 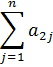
| |
| … | … | … | … | … | … | … | … | |||||
| ak | xk1 | ck1 | xk2 | ck2 | … | xkr | ckr | … | xkn | ckn | 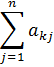
| |
| … | … | … | … | … | … | … | … | |||||
| am | xm1 | cm1 | xm2 | cm2 | … | xmr | cmr | … | xmn | cmn | 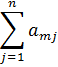
| |
|
|
| … |
| … |
| |||||||
При распределении товара по клеткам может оказаться, что количество занятых клеток меньше, чем m + n – 1 (m – количество пунктов отправления, n – количество пунктов назначения). Такой план называется вырожденным. В этом случае недостающее их число заполняется клетками с нулевыми поставками, такие клетки называют условно занятыми. Нулевые поставки помещают в пустые клетки с учетом наименьшей стоимости перевозки таким образом, чтобы в каждых строке и столбце было не менее чем по одной занятой клетке.
2) Проверка плана на оптимальность.
Проверить план на оптимальность можно с помощью метода потенциалов. Для этого к таблице опорного решения добавим столбец 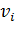 и строку
и строку 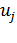 . Числа
. Числа 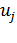 и
и 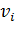 называют потенциалами. Рассчитываются потенциалы для занятых клеток по равенству
называют потенциалами. Рассчитываются потенциалы для занятых клеток по равенству 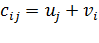 . Любому потенциалу сначала придаем значение любое значение (удобнее придать нулевое значение потенциалу
. Любому потенциалу сначала придаем значение любое значение (удобнее придать нулевое значение потенциалу 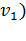 .
.
|
| bj | b1 | b2 | … | br | … | bn |
| ||||
| ai |
| |||||||||||
| a1 | x11 | c11 | x12 | c12 | … | x1r | c1r | … | x1n | c1n | 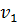
| |
| a2 | x21 | c21 | x22 | c22 | … | x2r | c2r | … | x2n | c2n | 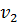
| |
| … | … | … | … | … | … | … | … | |||||
| ak | xk1 | ck1 | xk2 | ck2 | … | xkr | ckr | … | xkn | ckn | 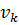
| |
| … | … | … | … | … | … | … | … | |||||
| am | xm1 | cm1 | xm2 | cm2 | … | xmr | cmr | … | xmn | cmn | 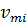
| |
|
|
|
| … |
| … |
| ||||||
Для всех свободных клеток рассчитаем напряженности, которые показывают возможность уменьшения цены. Напряженности рассчитываются по формуле: 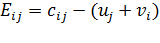 . Критерием оптимальности плана является отсутствие отрицательных напряженностей, то есть
. Критерием оптимальности плана является отсутствие отрицательных напряженностей, то есть 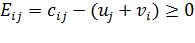 . Если есть хотя бы одна отрицательная напряженность, то план неоптимальный и его можно улучшить.
. Если есть хотя бы одна отрицательная напряженность, то план неоптимальный и его можно улучшить.
3) Переход от одного опорного решения к другому.
Переход от одного плана к другому осуществляется по циклу.
Цикл – замкнутая ломаная линия, состоящая из горизонтальных и вертикальных ребер, вершинами которой являются только заполненные ячейки, за исключением начала цикла. Цикл может иметь любую форму (примеры на рисунке 1.7).

Рис. 1.7. Примеры форм циклов
Начало цикла соответствует ячейке, у которой наибольшее по абсолютной величине отрицательное значение напряженности 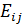 . Если таких ячеек несколько, то выбирается та ячейка, которой соответствует меньшая цена. Далее от начала цикла методом подбора по заполненным ячейкам составляем ребра цикла до тех пор, пока не вернемся в начало цикла. Цикл единственный.
. Если таких ячеек несколько, то выбирается та ячейка, которой соответствует меньшая цена. Далее от начала цикла методом подбора по заполненным ячейкам составляем ребра цикла до тех пор, пока не вернемся в начало цикла. Цикл единственный.
В начало цикла ставим (+), далее чередуем (-), (+) и т. д. Направление движения для чередования может быть любым.
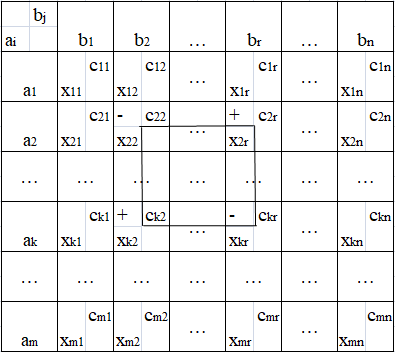
Из всех вершин цикла за знаком (-) выбираем наименьшее и в новом плане к ячейкам со знаком (+) прибавляем, а от ячеек со знаком (-) отнимаем. Остальные значения плана переписываем из предыдущего.
4) Проверяем план на оптимальность (п.2 алгоритма).
Пункты 2 – 4 алгоритма выполняем до тех пор, пока план не будет оптимальным.
При составлении опорного плана и при каждом переходе к новому плану необходимо рассчитывать стоимость перевозки по формуле
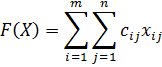
Значение стоимости перевозки с каждым переходом к новому плану должно уменьшаться. Если уменьшения не произошло, значит, была допущена ошибка.
Пример. Три фермерских хозяйства поставляют огурцы четырем оптовым покупателям. Ежедневная потребность покупателей составляет 10, 110, 40 и 110 ц соответственно. Фермерские хозяйства могут ежедневно поставлять 60, 120 и 100 ц огурцов соответственно. Матрица стоимостей перевозки 1 ц огурцов имеет вид 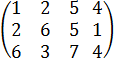 . Найти оптимальный план поставки огурцов.
. Найти оптимальный план поставки огурцов.
Решение.
1) Найдем опорный план, используя метод минимального элемента.
Проверим задачу на открытость.
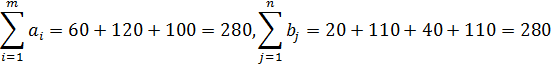
Следовательно, задача закрытая.
|
| 280 | 20 | 110 | 40 | 110 |
| ||||
| 280 |
| |||||||||
| 60 | 20 | 1 | 40 | 2 | х | 5 | х | 4 | 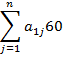
| |
| 120 | х | 2 | х | 6 | 10 | 5 | 110 | 1 | 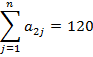
| |
| 100 | х | 6 | 70 | 3 | 30 | 7 | х | 4 | 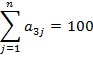
| |
|
|
|
|
| |||||||
Минимальная стоимость равна 1 в двух ячейках. Начинаем заполнять с ячейки, в которую можно записать большее значение, то есть с ячейки с индексом 23. Потребность третьего потребителя удовлетворена полностью, значит оставшиеся ячейки этого столбца заполняем знаком «х». Из оставшихся пустых ячеек выбираем наименьшую стоимость. Это 1. Заполняем соответствующую ячейку. Потребность первого потребителя удовлетворена полностью, значит, оставшиеся ячейки в данном столбце заполняем знаком «х». И так далее.
Заполнив все ячейки, проверим соответствие сумм по строкам и столбцам.
Рассчитаем стоимость перевозки: 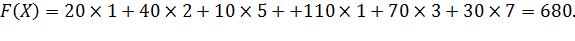
Посчитаем количество заполненных ячеек, их должно быть ровно m + n -1. В нашей таблице 6 заполненных ячеек, что соответствует условию, и задача является невырожденной.
2) Проверим план на оптимальность. Для этого дополним таблицу столбцом и строкой и рассчитаем потенциалы 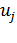 и
и 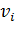 .
.
|
| 280 | 20 | 110 | 40 | 110 |
| ||||
| 280 |
| |||||||||
| 60 | 20 | 1 | 40 | 2 | х | 5 | х | 4 | 0 | |
| 120 | х | 2 | х | 6 | 10 | 5 | 110 | 1 | -1 | |
| 100 | х | 6 | 70 | 3 | 30 | 7 | х | 4 | 1 | |
|
| 1 | 2 | 6 | 2 | ||||||
Теперь рассчитаем напряженности для пустых клеток.
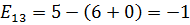 ,
,
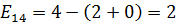 ,
,
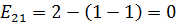 ,
,
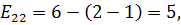
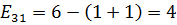 ,
,
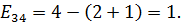
Так как есть отрицательное значение напряженности, то план является неоптимальным и его нужно улучшать.
3) Пересчитаем план.
Начало цикла будет в ячейке с индексов 13.
|
| 280 | 20 | 110 | 40 | 110 |
| ||||
| 280 |
| |||||||||
| 60 | 20 | 1 | -
40 |
| +
х | 5 | х | 4 | 0 | |
| 120 | х | 2 | х | 6 | 10 | 5 | 110 | 1 | -1 | |
| 100 | х | 6 | 70 | 3
+ | 30 | 7
- | х | 4 | 1 | |
|
| 1 | 2 | 6 | 2 | ||||||
Из всех значений в ячейках со знаком (-) выбираем меньшее и в новом плане к ячейкам со знаком (+) прибавляем 30, а от ячеек со знаком (-) отнимаем. Получим новый план.
|
| 280 | 20 | 110 | 40 | 110 |
| ||||
| 280 |
| |||||||||
| 60 | 20 | 1 | 10 | 2 | 30 | 5 | х | 4 | ||
| 120 | х | 2 | х | 6 | 10 | 5 | 110 | 1 | ||
| 100 | х | 6 | 100 | 3 | х | 7 | х | 4 | ||
|
| ||||||||||
Рассчитаем сумму стоимости перевозки. 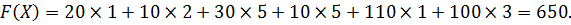 Стоимость перевозки уменьшилась, значит, расчеты проведены верно.
Стоимость перевозки уменьшилась, значит, расчеты проведены верно.
2) Проверим план на оптимальность.
Найдем потенциалы 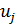 и
и 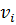 .
.
|
| 280 | 20 | 110 | 40 | 110 |
| ||||
| 280 |
| |||||||||
| 60 | 20 | 1 | 10 | 2 | 30 | 5 | х | 4 | 0 | |
| 120 | х | 2 | х | 6 | 10 | 5 | 110 | 1 | 0 | |
| 100 | х | 6 | 100 | 3 | х | 7 | х | 4 | 1 | |
|
| 1 | 2 | 5 | 1 | ||||||
Рассчитаем напряженности для пустых клеток.
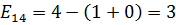 ,
,
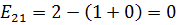 ,
,
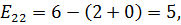
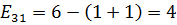 ,
,
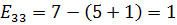 ,
,
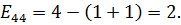
Среди найденных значений напряженностей нет отрицательных, следовательно, план оптимальный.
Ответ: минимальной суммой стоимости перевозки является 650. План перевозки:
Первый фермер поставляет 20 ц огурцов первому потребителю, 10 ц огурцов второму потребителю, 30 ц огурцов третьему потребителю.
Второй фермер поставляет 10 ц третьему потребителю и 110 ц четвертому потребителю.
Третий фермер поставляет 100 ц второму потребителю.
Рассмотрим транспортную задачу открытого типа ( 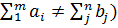 .
.
Решение транспортной задачи открытого типа сводится к решению транспортной задачи закрытого типа путем введения дополнительных (фиктивных) пунктов отправления или назначения с нулевыми стоимостями.
Если сумма имеющего товара в пунктах потребления больше суммы потребностей, то вводится фиктивный потребитель разницы. Если сумма потребностей больше суммы имеющего товара в пунктах отправления, то вводится фиктивный пункт отправления с нулевыми стоимостями. И далее задача решается так же, как задача закрытого типа.
Применение транспортной задачи
Транспортная задача может быть применены во многих социально-экономических областях. Существует множество прикладных социально-экономических задач, которые можно свести к транспортной задаче. Некоторые из таких задач приведены ниже.
Задача оптимального распределения работ. Требуется распределить m работ по n сотрудникам (отделам, участкам) так, чтобы суммарные затраты времени (финансов) были минимальными. Предполагается, что каждый сотрудник (отдел, участок) выполняет одну работу [17].
Задача оптимизации затрат на обучение персонала. Фирма располагает n группами должностей по 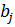 вакантных единиц в каждой группе; кандидаты на занятие должностей проходят тестирование, по результатам которого их разделяют на m групп по
вакантных единиц в каждой группе; кандидаты на занятие должностей проходят тестирование, по результатам которого их разделяют на m групп по 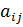 кандидатов в каждой группе; требуются затраты
кандидатов в каждой группе; требуются затраты 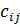 на обучение кандидата i-ой группы для занятия j-ой должности (если
на обучение кандидата i-ой группы для занятия j-ой должности (если 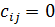 , кандидат полностью соответствует должности и обучение (переподготовка или повышение квалификации) не требуется, если
, кандидат полностью соответствует должности и обучение (переподготовка или повышение квалификации) не требуется, если 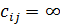 (или
(или 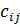 - любое заведомо большое число), кандидат не может занять данную должность). Требуется распределить кандидатов на должности, затратив минимальные средства на их обучение [17].
- любое заведомо большое число), кандидат не может занять данную должность). Требуется распределить кандидатов на должности, затратив минимальные средства на их обучение [17].
Задача оптимального распределения торговых агентов. Необходимо определить план продаж товара в нескольких городах с известной покупательной способностью жителей и известным профессиональным уровнем агентов, чтобы получить максимальный ожидаемый доход от продажи товаров [17].
Задача оптимального размещения производства. Требуется разработать план выпуска n новых видов продукции на m предприятиях при известных издержках производства и сбыта единицы продукции каждого вида, предполагаемом спросе на продукцию каждого вида и прогнозируемой цене за единицу продукции, максимизирующий ожидаемую прибыль [17].
Задача оптимального распределения оборудования. Оборудование различных видов нужно распределить между n рабочими участками так, чтобы суммарная производительность оказалась максимальной (производительность оборудования i -го вида на j-м участке равно 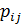 ) [17].
) [17].
Практическое занятие 8
Выучить алгоритм транспортной задачи.
Решить задачи.
1. На складах имеется товар в количестве А1=77, А2=53, А3=120, А4=60. В три магазина требуется товар в количестве В1=80, В2=80, В3=150. Матрица стоимостей 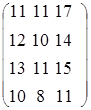 .
.
2. На складах имеется товар в количестве А1=80, А2=80, А3=50, А4=10. В четыре магазина требуется товар в количестве В1=65, В2=65, В3=75, В4=15. Матрица стоимостей 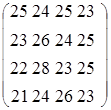 .
.
3. На складах имеется товар в количестве А1=60, А2=55, А3=120, А4=25. В четыре магазина требуется товар в количестве В1=75, В2=85, В3=80, В4=20. Матрица стоимостей 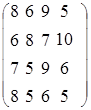 .
.
Домашнее задание:
1. Построить оптимальный план объемов перевозок по следующим условиям. На четырех складах имеется продукция в количестве: А1=200, А2=300, А3=250, А4=180. Для пяти магазинов требуется продукция в количестве: В1=150, В2=100, В3=200, В4=220, В5=210. Стоимость перевозок единицы продукции из i-го склада в j-ый магазин представлены в виде матрицы: 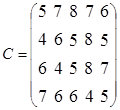 .
.
2. Построить оптимальный план объемов перевозок из трех складов в четыре магазина, если А1=150, А2=200, А3=180, В1=120, В2=100, В3=110, В4=200. Стоимость перевозок представлена в виде матрицы 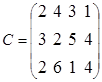 .
.
Дата: 2019-05-28, просмотров: 514.
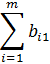
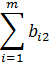
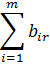
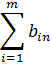
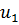
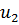
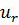
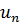
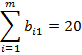
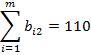
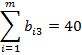
 2
2